一、单项选择题3. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB//CD,AD⊥DC,PD=AD=DC=2AB,则异面直线PA与BC所成角的余弦值为______
A.
B.
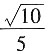
C.
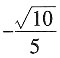
D.
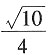
A B C D
B
[解析] 以D为坐标原点,分别以DA,DC,DP为x,y,z轴正方向建立空间坐标系。设PD=AD=DC=2AB=2,则P(0,0,2),A(2,0,0),B(2,1,0),C(0,2,0),故
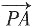
=(2,0,-2),
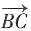
=(-2,1,0)。设异面直线PA与BC所成角为θ,则

6. 若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为______
A.
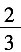
B.
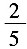
C.
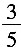
D.
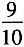
A B C D
D
[解析] 设“甲或乙被录用”为事件A,则其对立事件A表示“甲、乙两人都没有被录取”,则
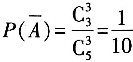
。因此
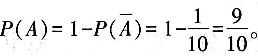
二、填空题1. 某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为______。
20%
[解析] 设这种商品平均每次降价的百分率为x。根据题意列方程得125(1-x)2=80,解得x1=0.2=20%,x2=-1.2(不合题意,舍去)。
2. 直线y=1与曲线y=x
2-|x|+a有四个交点,则a的取值范围是______。
[解析] 将本题等价转化为关于t的二次方程为t
2-t+a-1=0有两个不同的正数解,∴
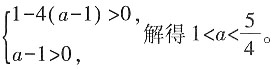
3. 甲、乙、丙三种溶液分别为
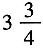
千克,
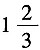
千克,
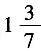
千克,现在将它们分别放入小瓶中,使得每个小瓶的溶液重量相等,至少可以装______瓶。
115
[解析]
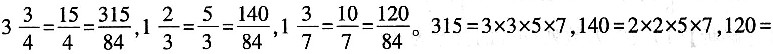
2×2×2×3×5,最大公约数是5,故1小瓶的溶液重量
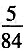
,至少可以装
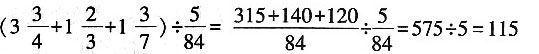
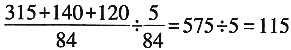
(瓶)。
4. (x-y)
10的展开式中,x
7y
3的系数与x
3y
7的系数之和等于______。
5. 若⊙O
1的圆心坐标为(2,0),半径为1,⊙O
2的圆心坐标为(-1,0),半径为3,则这两圆的位置关系是______。
相交
[解析] 根据题意,得两圆的圆心距为2-(-1)=3,两圆的半径之和为1+3=4,两圆的半径之差是3-1=2。由2<3<4,得两圆相交。
三、解答题某食品质量按行业标准可分为四个等级,等级系数x依次设为A、B、C、D.现从一批该食品中随机抽取20件,然后统计其等级系数的分布,得到频率分布表如下: 1. 若抽取的20件该食品,等级系数为A、C的件数比值为5:3,等级系数为D的有2件,求a,b,c的值;
解:由“等级系数为D的有2件”可得
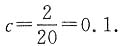
故等级系数为A和C的总频率为a+c=1-0.5-0.1=0.4.又因为等级系数为A、C的件数比值为5:3,即a:c=5:3,故a=
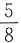
×0.4=0.25,b=
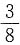
×0.4=0.15.
2. 在上一小题的条件下,将等级系数为A、B和C的食品(每一等级的产品各不相同)混合,从中抽取3件商品,其中3件商品全为同一等级和3件分属三个不同等级的概率分别是多少?
解:食品等级为A、B、C的件数共有20-2=18件,其中等级系数为A的件数为0.25×20=5件,等级系数为B的件数为0.5×20=10件,等级系数为C的件数为18-5-10=3件.
3件全属于同一等级系数的情况有3种:全为A的取法
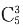
,全为B的取法
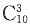
,全为C的取法
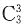
,总的取法有
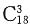
,故三件全属于同一等级的概率为
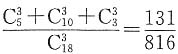
.
3件分属于三个不同等级的概率则为
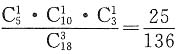
.
3. 若a,b互为相反数,c,d互为倒数,m是最大的负整数,求代数式

的值。
解:根据题意得a+b=0,cd=1,m=-1。
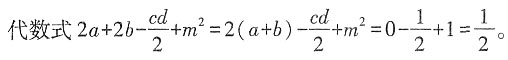
4. 设
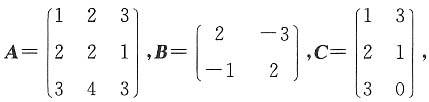
求矩阵X,使其满足AXB=C.
解:由题意可知,|A|≠0,|B|=1,故A、B均可逆,且
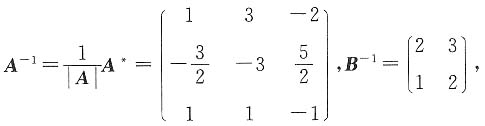
则
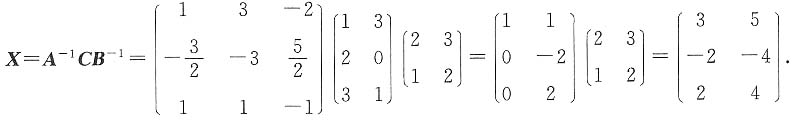
5. 在平面直角坐标系xOy中,已知点A(-2,0),点B在直线x=-6上,点M满足
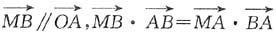
,求点M的轨迹方程C.
解:设M的坐标为(x,y),则由
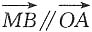
可知,B的坐标为(-6,y).
因为

,
又
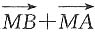
=(-6-x,0)+(-2-x,-y)=(-8-2x,-y),
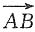
=(-4,y),
所以(-8-2x,-y)·(-4,y)=32+8x-y
2=0,即y
2=8x+32,
所以点M的轨迹方程C:y
2=8x+32.
6. 求证:点P
1(1,S
1/1),P
2(2,S
2/2),…,P
n(n,S
n/n)在同一条直线l
1上;
证:因为等差数列{a
n}的公差d≠0,
所以
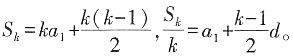
当k≥2(k∈N)时,
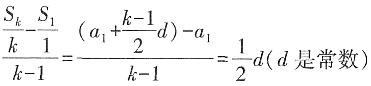
,即K
p1p2是常数(k=1,2,3,…,n)所以P
2,P
3,…,P
n都在过点P
1(1,a
1)且斜率为常数d/2的直线l
1上。
7. 过点Q
1(1,a
1),Q
2(2,a
2)作直线l
2,设l
1与l
2的夹角为θ,求证:
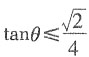
。
解:直线l
2的方程为y-a
1=d(x-1),直线l
2的斜率为d。
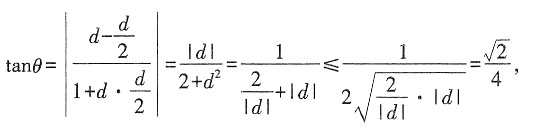
当且仅当
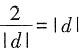
,即
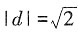
时等号成立。
8. 用“列表法”或“树状图法”表示所有可能出现的结果;
解:列表格如下:
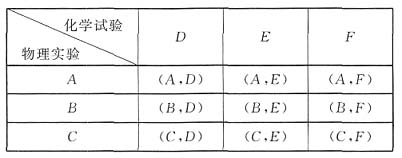
9. 小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?
解:从表格可以看出,所有可能出现的结果共有9种,其中事件M出现了一次,所以
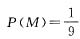
.
10.
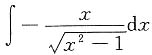
解:
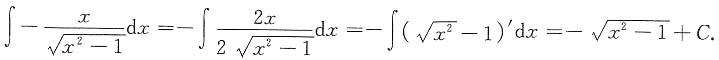
12.
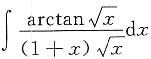
解:
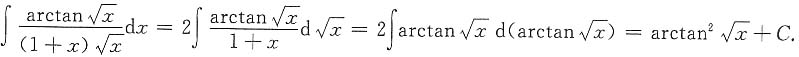
13.

解:

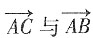 的夹角为______
的夹角为______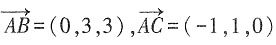 ,设
,设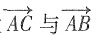 的夹角为θ,则
的夹角为θ,则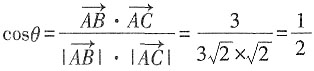 ,所以θ=60°。
,所以θ=60°。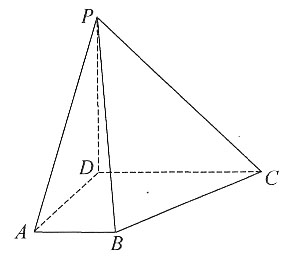
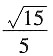
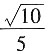
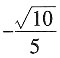
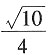
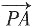 =(2,0,-2),
=(2,0,-2),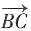 =(-2,1,0)。设异面直线PA与BC所成角为θ,则
=(-2,1,0)。设异面直线PA与BC所成角为θ,则
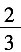
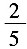
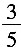
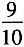
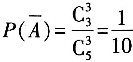 。因此
。因此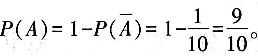
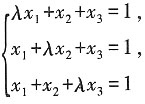 有唯一解,则______
有唯一解,则______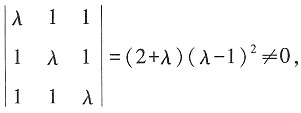 则λ≠1且λ≠-2。
则λ≠1且λ≠-2。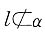 ,则______.
,则______. ,则有l/α,与题设相矛盾∴B正确C不正确;在α内不过l与α交点的直线与l异面,D不正确.
,则有l/α,与题设相矛盾∴B正确C不正确;在α内不过l与α交点的直线与l异面,D不正确.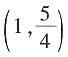
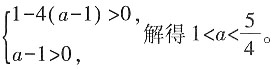
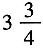 千克,
千克,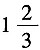 千克,
千克,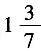 千克,现在将它们分别放入小瓶中,使得每个小瓶的溶液重量相等,至少可以装______瓶。
千克,现在将它们分别放入小瓶中,使得每个小瓶的溶液重量相等,至少可以装______瓶。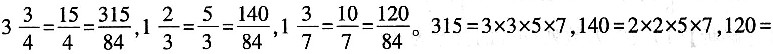 2×2×2×3×5,最大公约数是5,故1小瓶的溶液重量
2×2×2×3×5,最大公约数是5,故1小瓶的溶液重量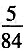 ,至少可以装
,至少可以装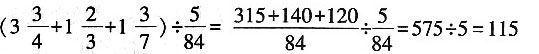
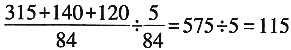 (瓶)。
(瓶)。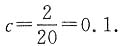 故等级系数为A和C的总频率为a+c=1-0.5-0.1=0.4.又因为等级系数为A、C的件数比值为5:3,即a:c=5:3,故a=
故等级系数为A和C的总频率为a+c=1-0.5-0.1=0.4.又因为等级系数为A、C的件数比值为5:3,即a:c=5:3,故a=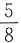 ×0.4=0.25,b=
×0.4=0.25,b=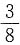 ×0.4=0.15.
×0.4=0.15.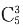 ,全为B的取法
,全为B的取法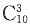 ,全为C的取法
,全为C的取法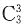 ,总的取法有
,总的取法有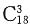 ,故三件全属于同一等级的概率为
,故三件全属于同一等级的概率为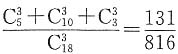 .
.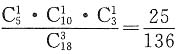 .
. 的值。
的值。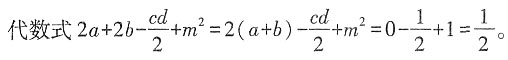
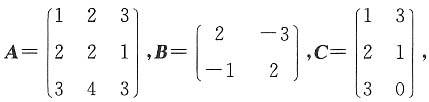 求矩阵X,使其满足AXB=C.
求矩阵X,使其满足AXB=C.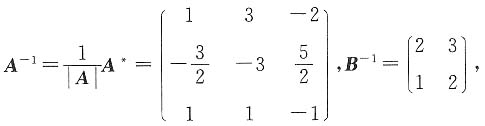
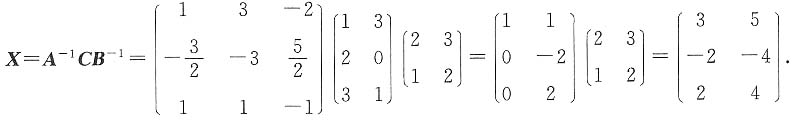
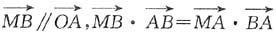 ,求点M的轨迹方程C.
,求点M的轨迹方程C.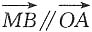 可知,B的坐标为(-6,y).
可知,B的坐标为(-6,y). ,
,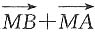 =(-6-x,0)+(-2-x,-y)=(-8-2x,-y),
=(-6-x,0)+(-2-x,-y)=(-8-2x,-y),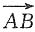 =(-4,y),
=(-4,y),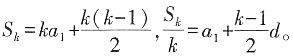
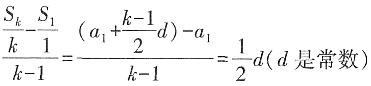 ,即Kp1p2是常数(k=1,2,3,…,n)所以P2,P3,…,Pn都在过点P1(1,a1)且斜率为常数d/2的直线l1上。
,即Kp1p2是常数(k=1,2,3,…,n)所以P2,P3,…,Pn都在过点P1(1,a1)且斜率为常数d/2的直线l1上。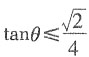 。
。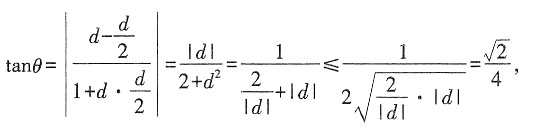
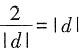 ,即
,即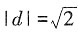 时等号成立。
时等号成立。
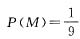 .
.
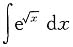
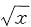 =t(t≥0),则有
=t(t≥0),则有