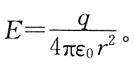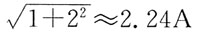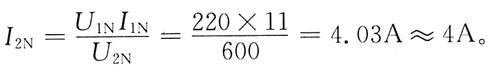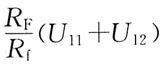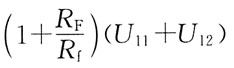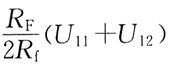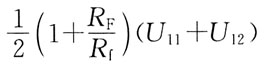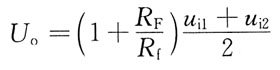单项选择题每题的备选项中只有一个最符合题意。
1. 设
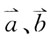
均为向量,下列等式中正确的是:
A.
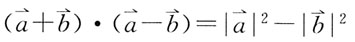
B.
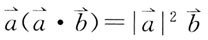
C.
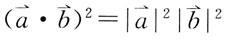
D.
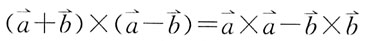
A B C D
A
[解析] 利用向量数量积的运算性质及两向量数量积的定义计算:
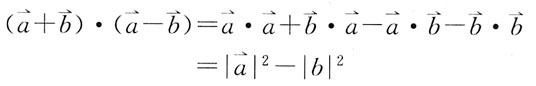
2. 过点M(3,-2,1)且与直线
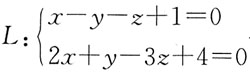
平行的直线方程是:
A.
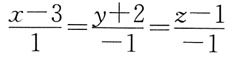
B.
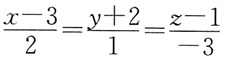
C.
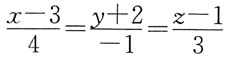
D.
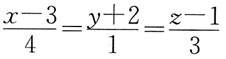
A B C D
D
[解析] 利用两向量的向量积求出直线L的方向向量:
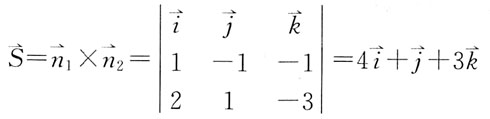
直线L过点M(3,-2,1),方向向量
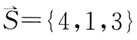
,再利用点向式写出直线L的方程为:
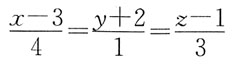
4. 将椭圆
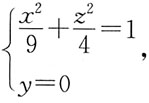
绕x轴旋转一周所生成的旋转曲面的方程是:
A.
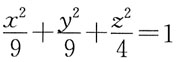
B.
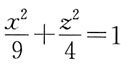
C.
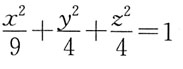
D.
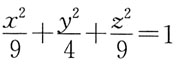
A B C D
C
[解析] 利用平面曲线方程和旋转曲面方程的关系直接写出。
如已知平面曲线
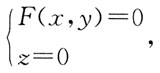
绕x轴旋转得到的旋转曲面方程为
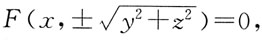
绕y轴旋转,旋转曲面方程为
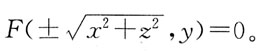
7. 设函数
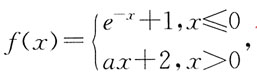
若f(x)在x=0处可导,则a的值是:
A B C D
D
[解析] 已知f(x)在x=0处可导,要满足f'
+(0)=f'
-(0)。
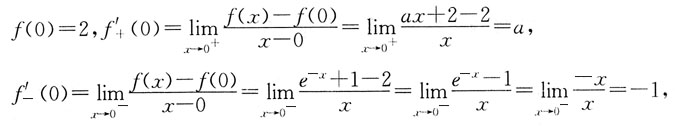
得a=-1(当x→0,e
-x-1~-x)。
8. 曲面z=x
2-y
2在点
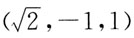
处的法线方程是:
A.
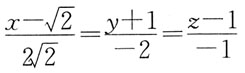
B.
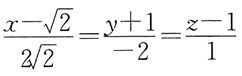
C.
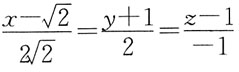
D.
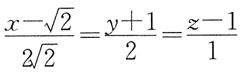
A B C D
C
[解析] 写成隐函数F(x,y,z)=0,即z-x
2+y
2=0。
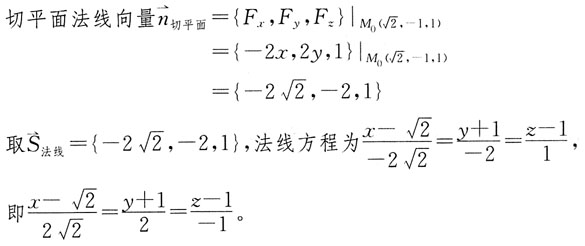
9. 下列结论中,错误的是:
A.
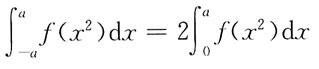
B.
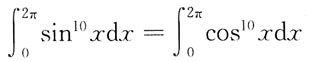
C.
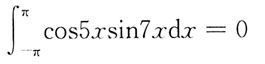
D.
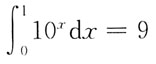
A B C D
D
[解析] 直接计算选项A、B、C较复杂,可先从简单选项入手,计算选项D,有
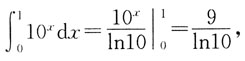
选项D错误。
选项A、B、C经计算,均成立。
10. 设平面闭区域D由

所围成,
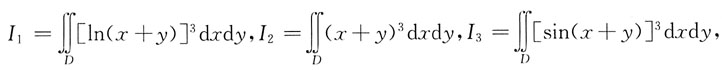
则I
1、I
2、I
3之间的关系应是:
- A.I1<I2<I3
- B.I1<I3<I2
- C.I3<I2<I1
- D.I3<I1<I2
A B C D
B
[解析] 为了观察方便,画出平面区域D的图形(见下图),区域D由直线x+y=1的下方,直线
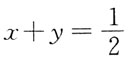
上方以及直线x=0,y=0围成。积分区域D上的点满足
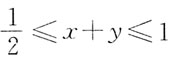
,故ln(x+y)≤0,[ln(x+y)]
3≤0。
由三角函数知识,当
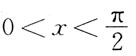
时,sinx
也即满足条件
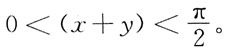
故0<sin(x+y)<x+y,0<[sin(x+y)]
3<(x+y)
3。
所以平面区域D上的点满足:
[ln(x+y)]
3<[sin(x+y)]
3<(x+y)
3 由二重积分性质:
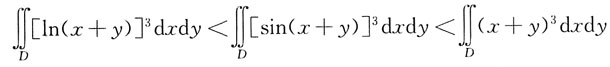
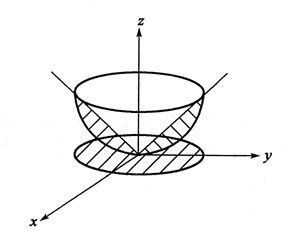
11. 由曲面
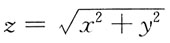
及z=x
2+y
2所围成的立体体积的三次积分为:
A.
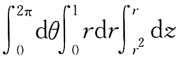
B.
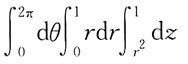
C.
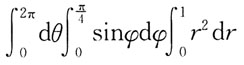
D.
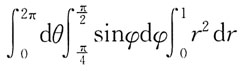
A B C D
A
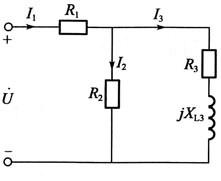
[解析] 画出图形,如图所示。求出投影区域D
xy。
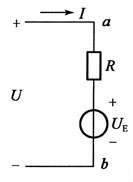
利用方程组
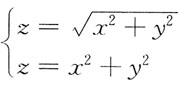
消去字母z,得D
xy:x
2+y
2≤1。
写出在柱面坐标系下计算立体体积的三次积分表示式:
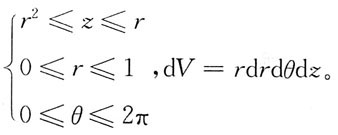
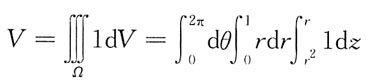
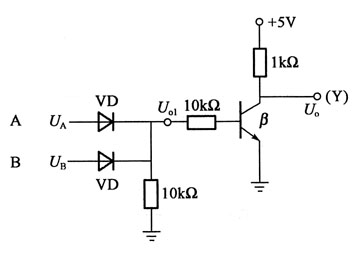
13. 级数

的收敛性是:
A B C D
A
[解析] 将级数各项取绝对值得
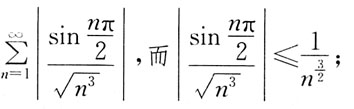
级数
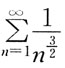
中,
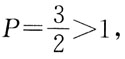
故收敛;
由正项级数比较法,级数
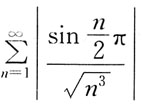
收敛;
所以原级数
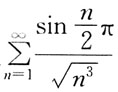
绝对收敛。
14. 级数
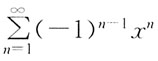
的和函数是:
A.
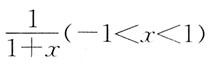
B.
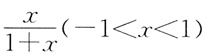
C.
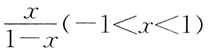
D.
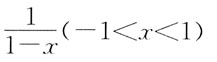
A B C D
B
[解析] 级数
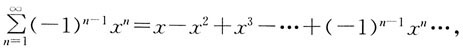
公比q=-x,当|q|<1时收敛。即|-x|<1,|x|<1,-1<x<1。
级数的和函数

15. 设
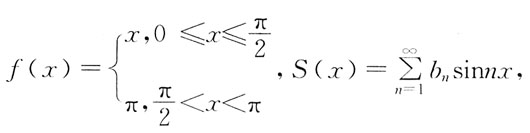
其中
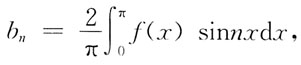
则
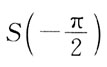
的值是:
A.
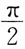
B.
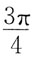
C.
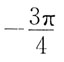
D.0
A B C D
C
[解析] 将函数奇延拓,并作周期延拓。画出在(-π,π)函数的图形,
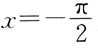
为函数的间断点。
由狄利克雷收敛定理:
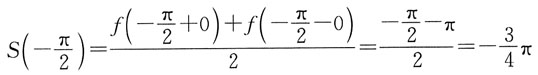
16. 级数
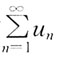
收敛的充要条件是:
A.
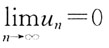
B.
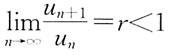
C.
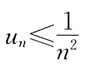
D.
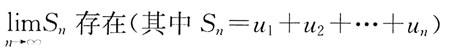
A B C D
D
[解析] 题中未说明级数是何种级数。
选项B、C仅适用于正项级数,故B、C不一定适用。
选项A为级数收敛的必要条件,不是充分条件。
选项D对任何级数都适用,是级数收敛的充要条件。
19. 设(X
1,X
2,…,X
10)是抽自正态总体N(μ,σ
2)的一个容量为10的样本,其中-∞<μ<+∞,σ
2>0,记
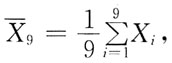
则
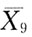
-X
10所服从的分布是:
A.
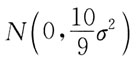
B.
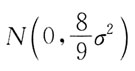
C.N(0,σ
2)
D.
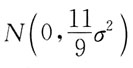
A B C D
A
[解析] X
1,X
2,…,X
10相互独立,且都服从N(μ,σ
2)分布,所以
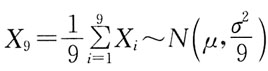
,
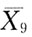
与X
10独立,
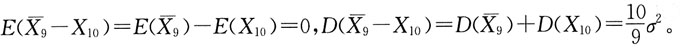
21. 设A和B都是n阶方阵,已知|A|=2,|B|=3,则|BA
-1|等于:
A.
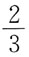
B.

C.6
D.5
A B C D
B
[解析] 利用矩阵行列式性质|BA
-1|=|B||A
-1|,又因为AA
-1=E,|A||A
-1|=1,所以
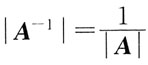
,故
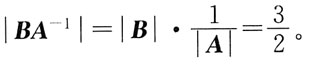
23. 设A为矩阵,
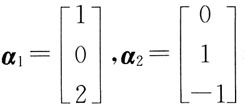
都是线性方程组Ax=0的解,则矩阵A为:
A.
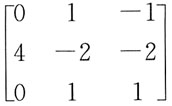
B.
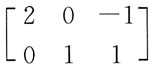
C.
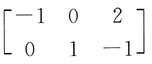
D.[-2,1,1]
A B C D
D
[解析] α
1,α
2是方程组Ax=0的两个线性无关的解,方程组含有3个未知量,故矩阵A的秩R(A)=3-2=1。选项A、B、C的秩分别为3、2、2,均不符合要求。将选项D代入方程组验证,

方程组解为

24. 设
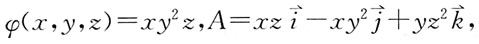
则
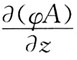
在点(-1,-1,1)处的值为:
A.
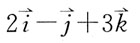
B.
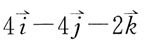
C.
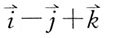
D.
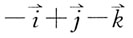
A B C D
A
[解析]
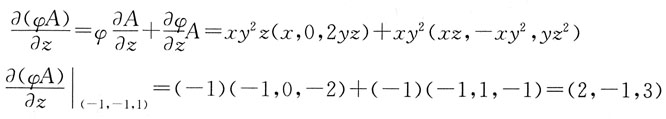
25. 一定质量的理想气体,在温度不变的条件下,当压强降低时,分子的平均碰撞次数
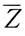
和平均自由程
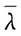
的变化情况是:
A.

B.

C.
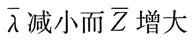
D.
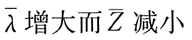
A B C D
D
[解析]
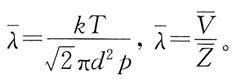
注意:温度不变,
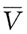
不变。
30. 若一平面简谐波的波动方程为y=Acos(Bt-Cx),式中A、B、C为正值恒量,则:
A.波速为C
B.

C.
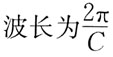
D.

A B C D
C
[解析] 比较波动方程
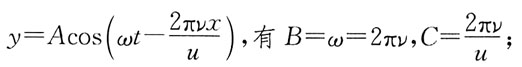
因此
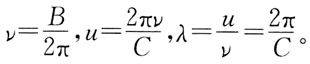
33. 波长为λ的单色平行光垂直入射到一狭缝上,若第一级暗纹的位置对应的衍射角为
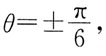
则缝宽的大小为:
A.
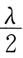
B.λ
C.2λ
D.3λ
A B C D
C
[解析]
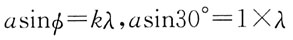
35. 如果两个偏振片堆叠在一起,且偏振化方向之间夹角为60°,假设两者对光无吸收,光强为I
0的自然光垂直入射到偏振片上,则出射光强为:
A.
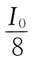
B.
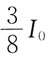
C.
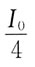
D.
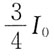
A B C D
A
[解析] I=I
0cos
2α(注意:自然光通过偏振片后,光强减半。)
出射光强
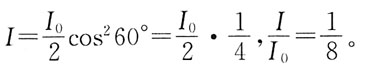
36. 有两种理想气体,第一种的压强记作p
1,体积记作V
1,温度记作T
1,总质量记作m
1,摩尔质量记作M
1;第二种的压强记作p
2,体积记作V
2,温度记作T
2,总质量记作行m
2,摩尔质量记作M
2。当V
1=V
2,T
1=T
2,m
1=m
2时,则
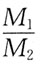
为:
A.
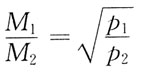
B.
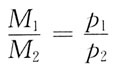
C.
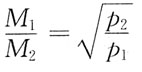
D.

A B C D
D
[解析] 由
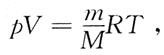
今V
1=V
2,T
1=T
2,m
1=m
2,故
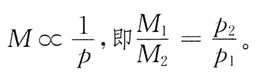
39. 用杂化轨道理论推测下列分子的空间构型,其中为平面三角形的是:
A B C D
B
[解析] B原子的价电子为
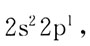
当B原子与F原子形成化学键的过程中,一个2s轨道上的电子跃迁到2p轨道上,采取sp
2杂化形成三个sp
2杂化轨道,三个sp
2杂化轨道采取最大夹角原则在空间伸展,形成平面三角形排布。故BF
3为三角形。
45. 对于化学反应3Cl
2+6NaOH=NaClO
3+5NaCl+3H
2O,下列叙述正确的是:
- A.Cl2既是氧化剂,又是还原剂
- B.Cl2是氧化剂,不是还原剂
- C.Cl2是还原剂,不是氧化剂
- D.Cl2既不是氧化剂,又不是还原剂
A B C D
A
[解析] 氧化还原反应中,失去电子的物质为还原剂,得到电子的物质为氧化剂。此反应中,Cl
2中氯元素的氧化值既有降低生成Cl
-,又有升高生成
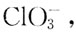
所以Cl
2既是氧化剂,又是还原剂。
48. 已知乙酸与乙酸乙酯的混合物中氢(H)的质量分数为7%,其中碳(C)的质量分数是:
- A.42.0%
- B.44.0%
- C.48.6%
- D.91.9%
A B C D
A
[解析] 设混合物中乙酸的质量分数约为x,则乙酸乙酯的质量分数为1-x,乙酸中的H的质量分数=
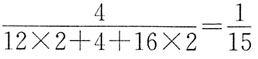
,则C的质量分数=
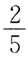
;乙酸乙酯中H的质量分数=
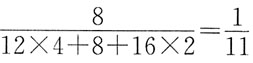
;C的质量分数=
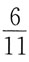
。
混合物中H的质量分数=
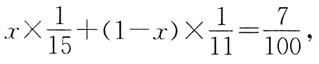
则x=87.5%;
混合物中C的质量分数=
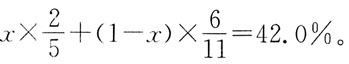
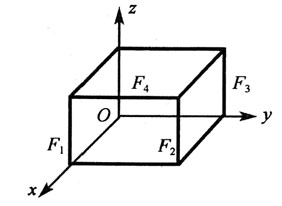
49. 平面汇交力系
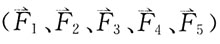
的力多边形如图所示,该力系的合力
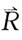
等于:
A.
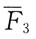
B.
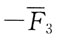
C.
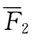
D.
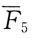
A B C D
B
[解析] 平面汇交力系几何法合成,各分力首尾相连,力多边形的封闭边是合力。
56. 四连杆机构运动到图示位置时,AB//O
1O
2,O
1A杆的角速度为ω
1,则O
2B杆的角速度ω
2为:
- A.ω2=0
- B.ω2<ω1
- C.ω2>ω1
- D.ω2=ω1
A B C D
D
[解析] 对杆AB应用速度投影定理,得到A、B两点速度的关系;再由
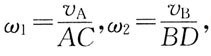
得到ω
1和ω
2两个角速度之间的关系。
60. 均质细直杆OA长为l,质量为m,A端固结一质量为m的小球(不计尺寸),如图所示。当OA杆以匀角速度ω绕O轴转动时,该系统对O轴的动量矩为:
A.
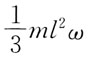
B.
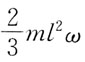
C.ml
2ω
D.
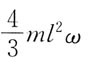
A B C D
D
[解析] 动量矩
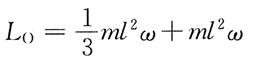
61. 在下图中,将系统的惯性力系向O点简化,其主矢F
1和主矩M
IO的数值分别为:
A.
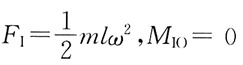
B.

C.
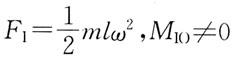
D.
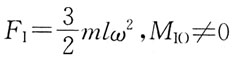
A B C D
B
[解析] 惯性力系向O点简化时,FI=maC,MIO=JOα。
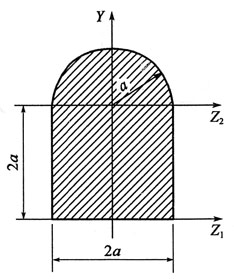
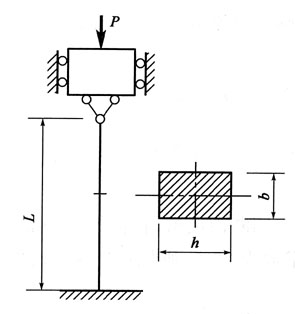
68. 梁的横截面形状如图所示,则截面对Z轴的抗弯截面模量W
z为:
A.
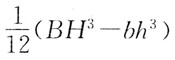
B.
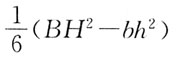
C.
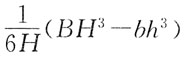
D.
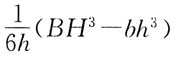
A B C D
C
[解析] 根据定义,
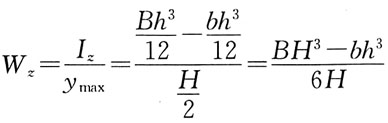
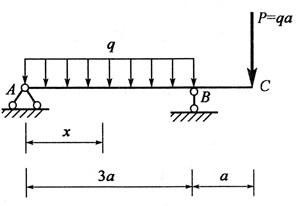
70. 图示梁,剪力等于零的截面位置x之值为:
A.
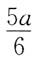
B.
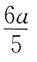
C.
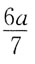
D.
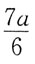
A B C D
D
[解析] 首先求支反力,设F
A向上,取整体平衡:
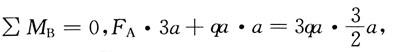
所以
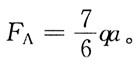
由F
S(x)=F
A-qx=0,得
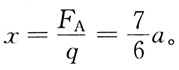
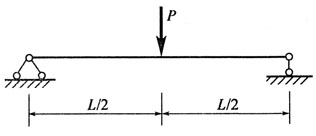
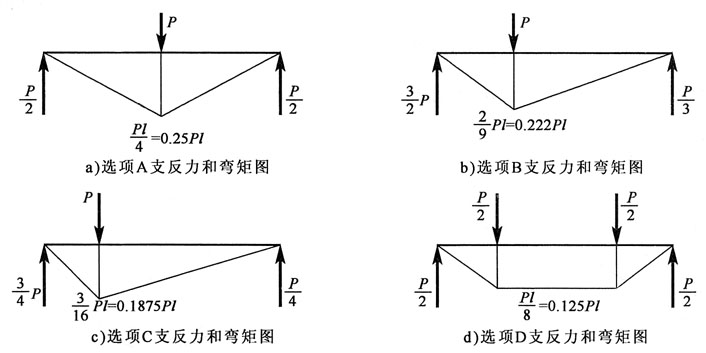
71. 就正应力强度而言,以下梁中,哪个图所示的加载方式最好?
A.
B.
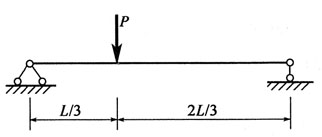
C.
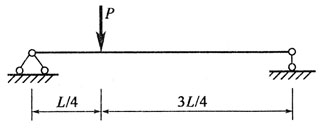
D.
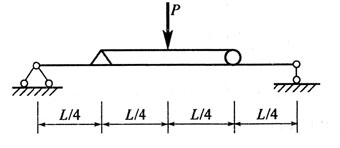
A B C D
D
[解析] 题图所示四个梁,其支反力和弯矩图分别如题解图所示。
就梁的正应力强度条件而言,
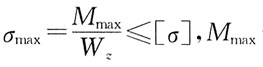
越小σ
max越小,梁就越安全。题述四个弯矩图中显然选项d)图M
max最小。
76. 一端固定,一端为球形铰的大柔度压杆,横截面为矩形(如图所示),则该杆临界力P
cr为:
A.
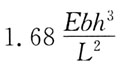
B.
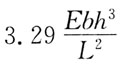
C.

D.
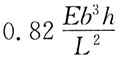
A B C D
C
[解析] 压杆临界力公式中的惯性矩应取压杆横截面上的最小惯性矩I
min,
故
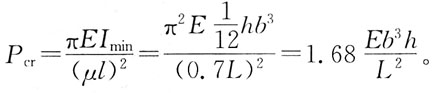
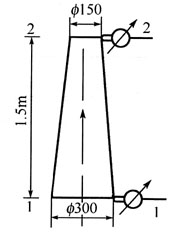
81. 如图所示,有一垂直放置的渐缩管,内径d
1=300mm渐缩至d
2=150mm,水从下而上自粗管流入细管。测得水在粗管1-1断面和细管2-2断面处的相对压强分别为98kPa和60kPa,两断面间垂直距离为1.5m,若忽略摩擦阻力,则通过渐缩管的流量为:
- A.0.125m3/s
- B.0.25m3/s
- C.0.50m3/s
- D.1.00m3/s
A B C D
A
[解析] 用能量方程和连续方程求出平均流速v,则流量Q=vA。
对断面1-1,2-2写能量方程,有
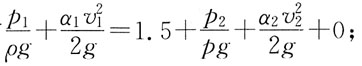
又由连续方程得:
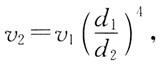
代入上式中,并代入题设数据。
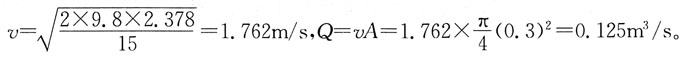
82. 如图所示,一压力水管渐变段,水平放置,已知d
1=1.5m,d
2=1m,渐变段开始断面相对压强p
1=388kPa,管中通过流量Q=2.2m
3/s,忽略水头损失,渐变段支座所受的轴心力为:
- A.320kN
- B.340kN
- C.360kN
- D.380kN
A B C D
D
[解析] 联合运用连续方程、能量方程、动量方程以及流量公式Q=vA。
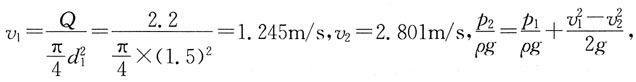
所以
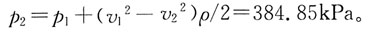
列动量方程∑F
x=ρQ(v
2x-v
1x),p
1A
1-p
2A
2-R=ρQ(v
2-v
1)。
反力
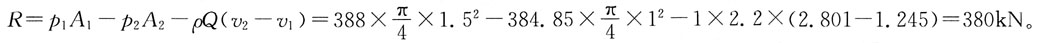
83. 圆管层流运动过流断面上速度分布为:(式中r
0为网管半径)
A.
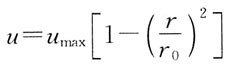
B.
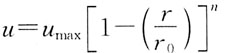
C.
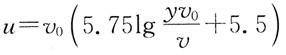
D.

A B C D
A
[解析] 参看圆管层流运动流速分布相关内容(流速分布曲线为二次抛物线)。
85. 圆管紊流粗糙区(阻力平方区)的沿程摩阻系数λ与:
A.雷诺数Re有关
B.相对粗糙度
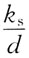
有关
C.雷诺数Re和相对粗糙度

有关
D.雷诺数Re和管长l有关
A B C D
B
[解析] 参看紊流沿程阻力系数相关内容(在阻力平方区,沿程阻力系数与相对粗糙度
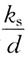
有关)。
96. 阅读以下FORTRAN程序
READ(*,*)M,N
K=MOD(M,N)
10 IF(K.GT.0)THEN
M=N
N=K
K=MOD(M,N)
GOTO 10
ENDIF
WRITE(*,*)N
END
若运行以上程序时,由键盘输入25.11,则程序输出为:
A B C D
97. 以下子例行程序用于实现向一维数组下标为P的数组元素处插入一个整数X
SUBROUTINE INSERT(B,N,P,X)
INTEGER B(N),X,P
DO 20K=N-1,P,-1
B(K+1)=______
20 CONTINUE
B(P)=X
END
为使程序完整,应在______处放入:
A B C D
98. 阅读下列FORTRAN程序
INTEGER X(3,3),A
DATA X/1,2,3,4,5,6,7,8,9/
DO 10 I=1.3
DO 10 J=1+1.3
A=X(I,J)
X(I,J)=X(J,I)
X(J,I)=A
10 CONTINUE
WRITE(*,20)((X(I,J),J=1,3)I=1,3)
20 PORMAT(IX,312)
END
运行上述程序后,其输出是:
A.

B.

C.

D.

A B C D
B
[解析] 开始赋值按列主序赋值:X(1,1)=1,2,X(3,1)=3,X(1,2)=4,X(2,2)=5,X(3,2)=6,X(1,3)=7,X(2,3)=8,X(3,3)=9。
第一次循环:I=1,J=2,A=X(1,2)=4,X(1,2)=X(2,1)=2,X(2,1)=4,以此类推得到结果。
99. 以点电荷q所在点为球心,距点电荷q的距离为r处的电场强度E应为:
A.
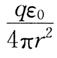
B.
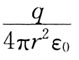
C.
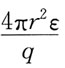
D.
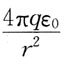
A B C D
B
[解析] 电场强度公式
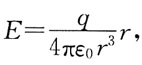
取绝对值
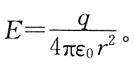
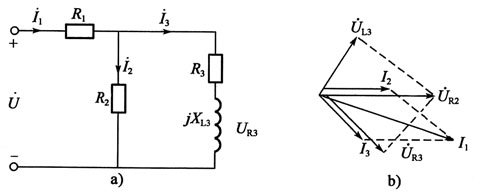
102. 图示电路,正弦电流i
2的有效值I
2=1A,电流i
3的有效值I
3=2A,因此电流i
1的有效值I
1等于:
A.
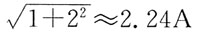
B.1+2=3A
C.2-1=1A
D.不能确定
A B C D
D
[解析] 首先画出该电路的复数电路图,见解图a),然后画相量图分析,见解图b),可见,由于电参数未定,各相量之间的关系不定。
注意此题可以用“排除法”完成,分析会简单些。
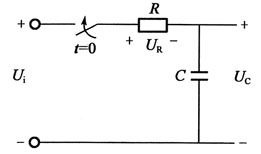
104. 图示电路中,换路前U
C(0-)=0.2U
i,U
R(0-)=0,电路换路后U
C(0+)和U
R(0+)分别为:
- A.UC(0+)=0.2Ui,UR(0+)=0
- B.UC(0+)=0.2Ui,UR(0+)=0.2Ui
- C.UC(0-)=0.2Ui,UR(0+)=0.8Ui
- D.UC(0+)=0.2U1,UR(0+)=Ui
A B C D
C
[解析] 根据换路定则:UC(0+)=UC(0-)=0.2Ui,UR(0+)=Ui-UC(0+)=0.8Ui。
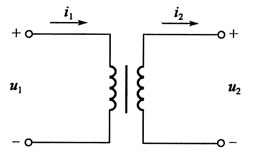
105. 图示变压器,一次额定电压U
1N=220V,一次额定电流I
1N=11A,二次额定电压U
2N=600V。该变压器二次额定值I
2N约为:
A B C D
B
[解析] 该题可以按理想变压器分析(即变压器内部的损耗为0),则I
1NU
1N=I
2NU
2N因此
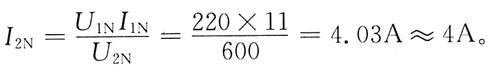
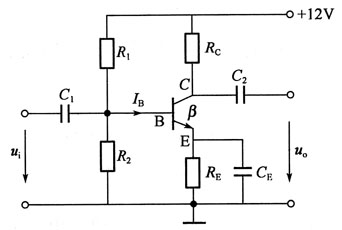
108. 如图所示电路中,R
1=50kΩ,R
2=10kΩ,R
E=1kΩ,R
C=5kΩ,晶体管的β=60,静态U
BE=0.7V。静态基极电流I
B等于:
- A.0.0152mA
- B.0.0213mA
- C.0.0286mA
- D.0.0328mA
A B C D
B
[解析] 根据放大电路的直流通道分析,直流通道如解图所示。
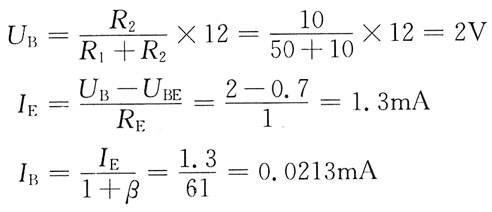
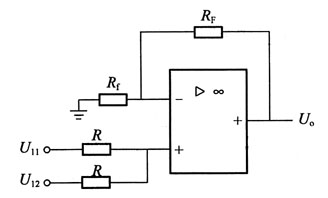
109. 图示电路中,输出电压U
o与输入电压U
11、U
12的关系式为:
A.
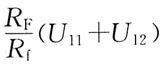
B.
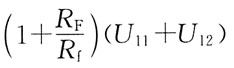
C.
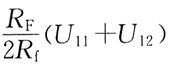
D.
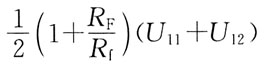
A B C D
D
[解析] 因为
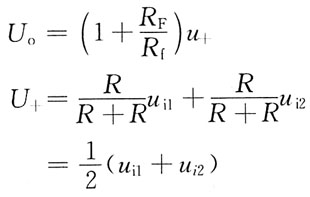
所以
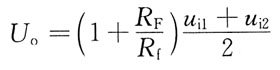
110. 图示电路中,二极管视为理想元件,即正向电压降为零,反向电阻为无穷大。三极管的β=100。输入信号U
A、U
B的高电平是3.5V(逻辑1),低电平是0.3V(逻辑0),若该电路的输出电压U
o为电压平时定为逻辑1,图示电路应为:
A B C D
D
[解析] 当U
A或U
B中有高电位时,U
o1输出高电位,U
o1与U
A、U
B符合或门逻辑电路。U
o与U
o1的电位关系符合非门逻辑,因此,该电路的输出与输入之间有或非逻辑。电位分析见表1和表2。
| 表1
|
| UA
|
UB
|
Uo
|
| 0.3V
|
0.3V
|
5V
|
| 0.3V
|
3.5V
|
0.3V
|
| 3.5V
|
0.3V
|
0.3V
|
| 3.5V
|
3.5V
|
0.3V
|
| 表2
|
| A
|
B
|
Y
|
| 0
|
0
|
1
|
| 0
|
1
|
0
|
| 1
|
0
|
0
|
| 1
|
1
|
0
|
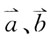 均为向量,下列等式中正确的是:
均为向量,下列等式中正确的是: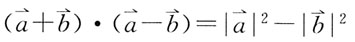
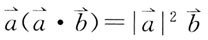
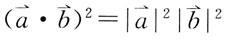
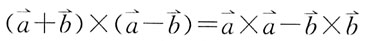
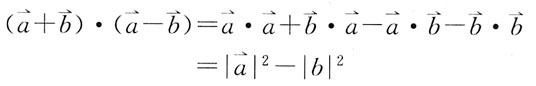
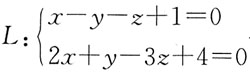 平行的直线方程是:
平行的直线方程是: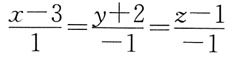
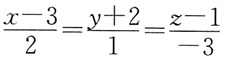
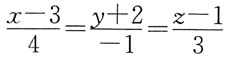
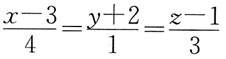
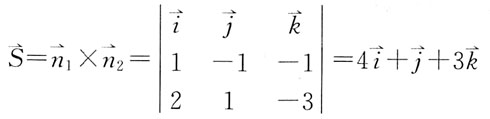
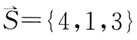 ,再利用点向式写出直线L的方程为:
,再利用点向式写出直线L的方程为: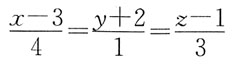
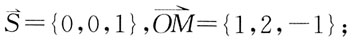
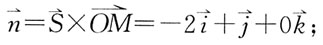
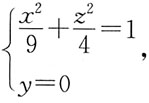 绕x轴旋转一周所生成的旋转曲面的方程是:
绕x轴旋转一周所生成的旋转曲面的方程是: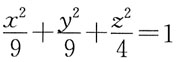
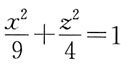
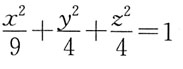
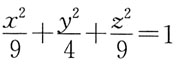
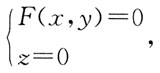 绕x轴旋转得到的旋转曲面方程为
绕x轴旋转得到的旋转曲面方程为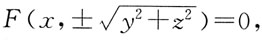 绕y轴旋转,旋转曲面方程为
绕y轴旋转,旋转曲面方程为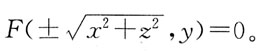
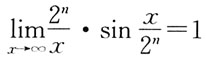

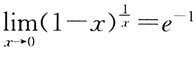
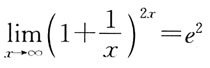
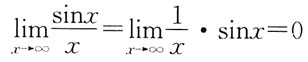
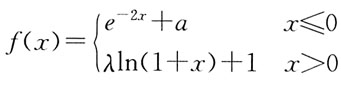 ,要使f(x)在x=0处连续,则a的值是:
,要使f(x)在x=0处连续,则a的值是: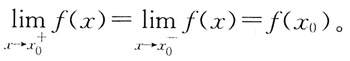
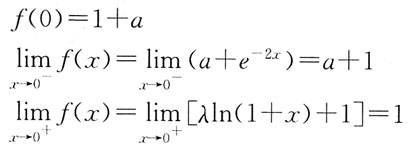
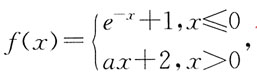 若f(x)在x=0处可导,则a的值是:
若f(x)在x=0处可导,则a的值是: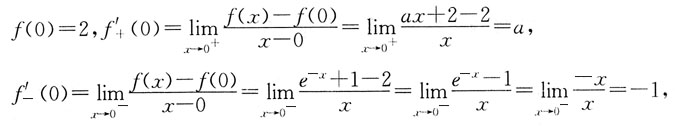
 处的法线方程是:
处的法线方程是: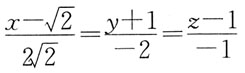
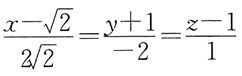
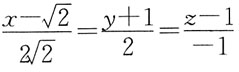
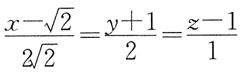
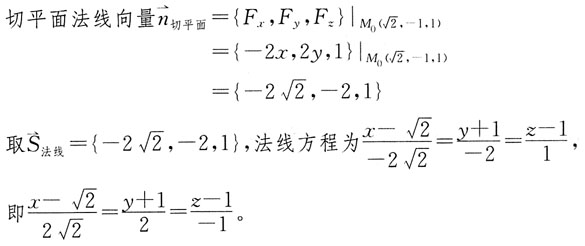
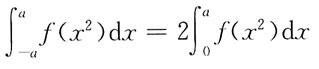
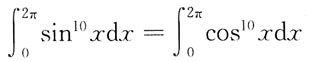
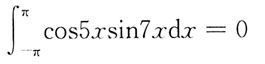
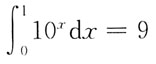
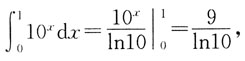 选项D错误。
选项D错误。 所围成,
所围成,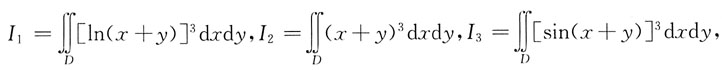 则I1、I2、I3之间的关系应是:
则I1、I2、I3之间的关系应是: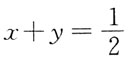 上方以及直线x=0,y=0围成。积分区域D上的点满足
上方以及直线x=0,y=0围成。积分区域D上的点满足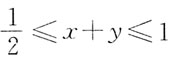 ,故ln(x+y)≤0,[ln(x+y)]3≤0。
,故ln(x+y)≤0,[ln(x+y)]3≤0。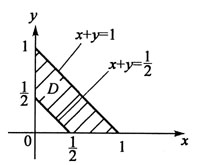
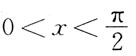 时,sinx
时,sinx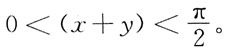 故0<sin(x+y)<x+y,0<[sin(x+y)]3<(x+y)3。
故0<sin(x+y)<x+y,0<[sin(x+y)]3<(x+y)3。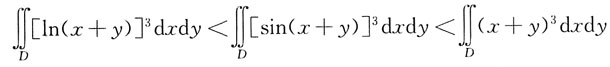
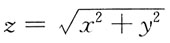 及z=x2+y2所围成的立体体积的三次积分为:
及z=x2+y2所围成的立体体积的三次积分为: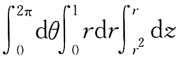
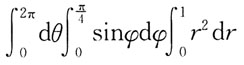
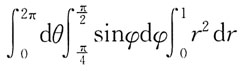
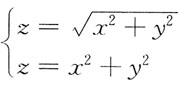 消去字母z,得Dxy:x2+y2≤1。
消去字母z,得Dxy:x2+y2≤1。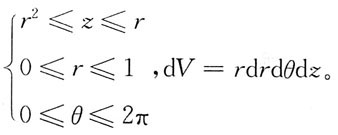
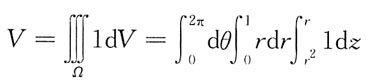
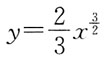 上相应于x从0到1的一段弧的长度是:
上相应于x从0到1的一段弧的长度是: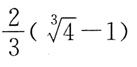
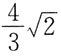
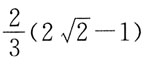
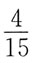
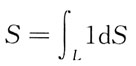
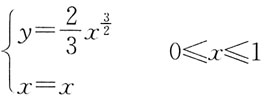
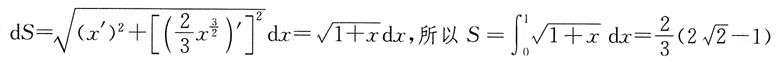
 的收敛性是:
的收敛性是: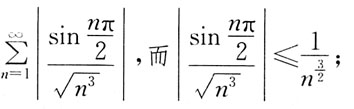
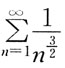 中,
中,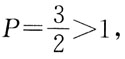 故收敛;
故收敛;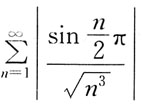 收敛;
收敛;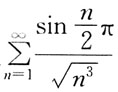 绝对收敛。
绝对收敛。 的和函数是:
的和函数是: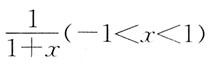
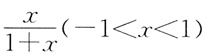
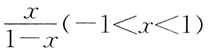
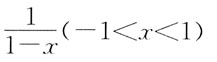
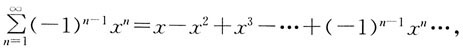 公比q=-x,当|q|<1时收敛。即|-x|<1,|x|<1,-1<x<1。
公比q=-x,当|q|<1时收敛。即|-x|<1,|x|<1,-1<x<1。
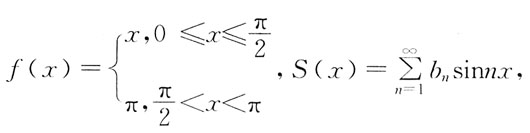 其中
其中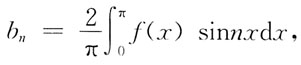 则
则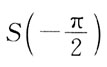 的值是:
的值是: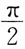
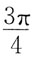
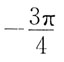
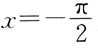 为函数的间断点。
为函数的间断点。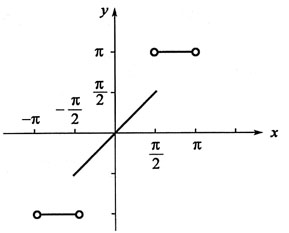
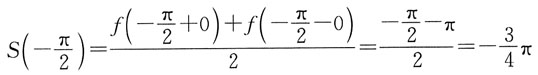
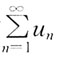 收敛的充要条件是:
收敛的充要条件是:
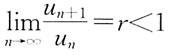
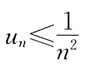
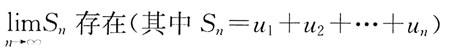
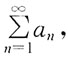 判定
判定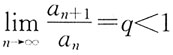 是此正项级数收敛的什么条件?
是此正项级数收敛的什么条件?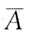 表示:
表示: 表示“第一次成功”,
表示“第一次成功”, 表示“第二次失败”。
表示“第二次失败”。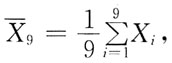 则
则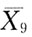 -X10所服从的分布是:
-X10所服从的分布是: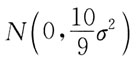
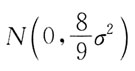
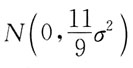
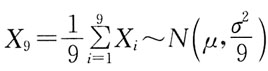 ,
,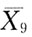 与X10独立,
与X10独立,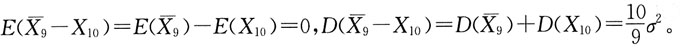
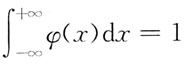
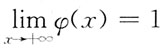
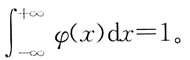
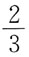

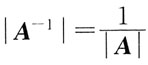 ,故
,故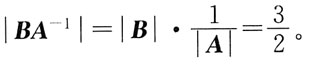
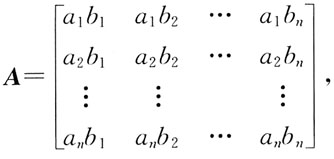 其中ai≠0,bi≠0(i=1,2,…,n),则矩阵A的秩等于:
其中ai≠0,bi≠0(i=1,2,…,n),则矩阵A的秩等于: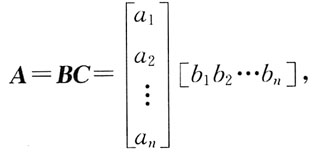 由矩阵的性质可知,R(BC)≤min[R(B),R(C)],因R(B)=1,R(C)=1,而A是非零矩阵,故R(A)=R(BC)=1。
由矩阵的性质可知,R(BC)≤min[R(B),R(C)],因R(B)=1,R(C)=1,而A是非零矩阵,故R(A)=R(BC)=1。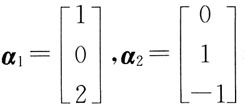 都是线性方程组Ax=0的解,则矩阵A为:
都是线性方程组Ax=0的解,则矩阵A为: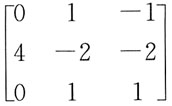
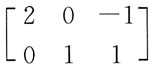
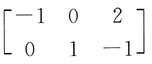
 方程组解为
方程组解为
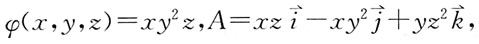 则
则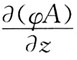 在点(-1,-1,1)处的值为:
在点(-1,-1,1)处的值为: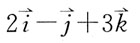
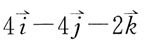
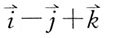
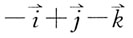
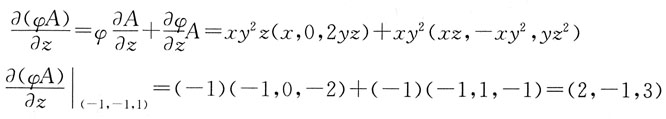
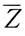 和平均自由程
和平均自由程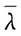 的变化情况是:
的变化情况是:

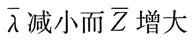
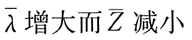
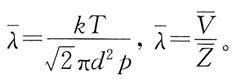 注意:温度不变,
注意:温度不变,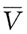 不变。
不变。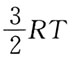
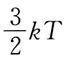

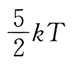
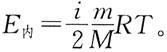
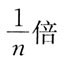
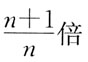
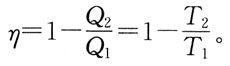

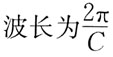

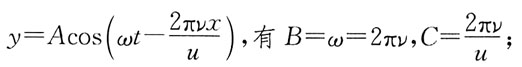
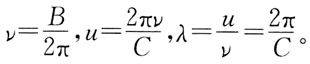
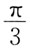 ,则此两点相距:
,则此两点相距: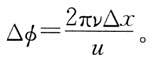
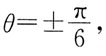 则缝宽的大小为:
则缝宽的大小为: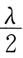
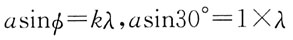
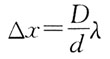
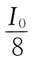
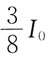
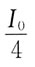
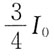
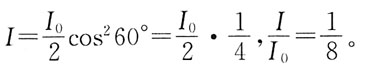
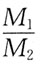 为:
为: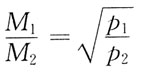
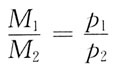
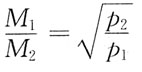

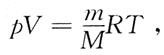 今V1=V2,T1=T2,m1=m2,故
今V1=V2,T1=T2,m1=m2,故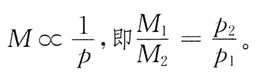
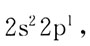 当B原子与F原子形成化学键的过程中,一个2s轨道上的电子跃迁到2p轨道上,采取sp2杂化形成三个sp2杂化轨道,三个sp2杂化轨道采取最大夹角原则在空间伸展,形成平面三角形排布。故BF3为三角形。
当B原子与F原子形成化学键的过程中,一个2s轨道上的电子跃迁到2p轨道上,采取sp2杂化形成三个sp2杂化轨道,三个sp2杂化轨道采取最大夹角原则在空间伸展,形成平面三角形排布。故BF3为三角形。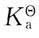 是:
是: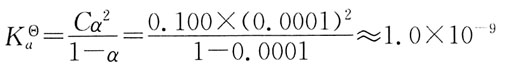
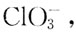 所以Cl2既是氧化剂,又是还原剂。
所以Cl2既是氧化剂,又是还原剂。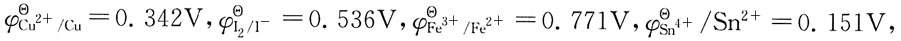 试判断下列还原剂的还原性由强到弱的是:
试判断下列还原剂的还原性由强到弱的是: 下列说法不正确的是:
下列说法不正确的是: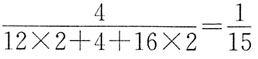 ,则C的质量分数=
,则C的质量分数=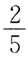 ;乙酸乙酯中H的质量分数=
;乙酸乙酯中H的质量分数=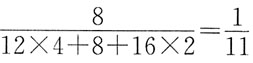 ;C的质量分数=
;C的质量分数=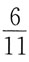 。
。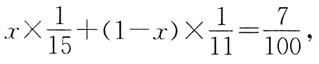 则x=87.5%;
则x=87.5%;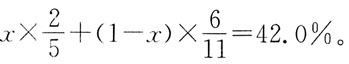
 的力多边形如图所示,该力系的合力
的力多边形如图所示,该力系的合力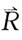 等于:
等于:
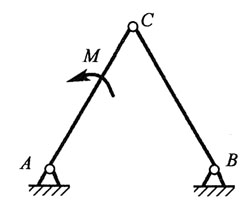
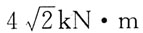
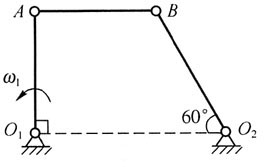
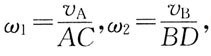 得到ω1和ω2两个角速度之间的关系。
得到ω1和ω2两个角速度之间的关系。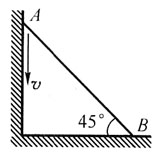

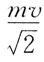

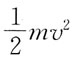

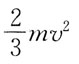
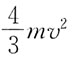
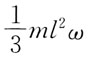
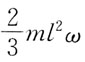
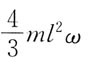
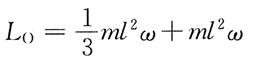

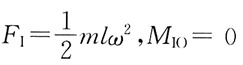

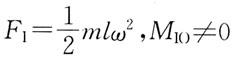
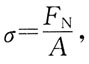 轴向变形
轴向变形 若横截面面积A和其他条件不变,则内力、应力、轴向变形均不变。
若横截面面积A和其他条件不变,则内力、应力、轴向变形均不变。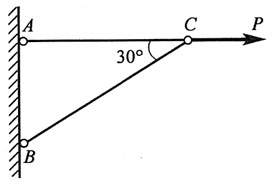
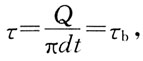 故冲力F=Q-πdτb。
故冲力F=Q-πdτb。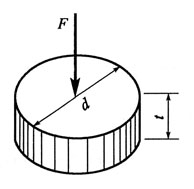
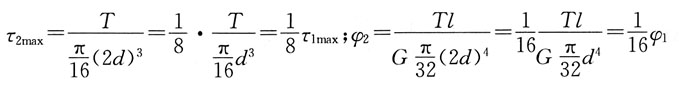
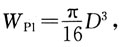 空心圆轴截面的抗扭截面模量
空心圆轴截面的抗扭截面模量 当外径D相同时,显然WP1>WP2。
当外径D相同时,显然WP1>WP2。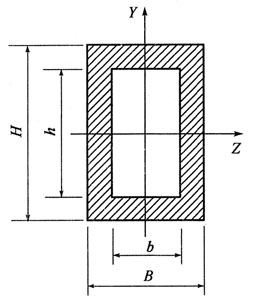
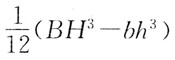
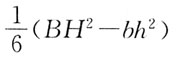
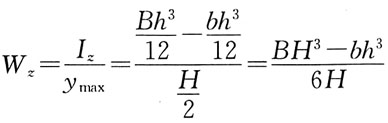
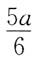
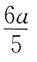
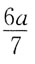
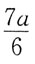
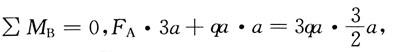 所以
所以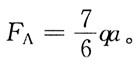 由FS(x)=FA-qx=0,得
由FS(x)=FA-qx=0,得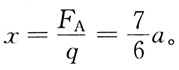




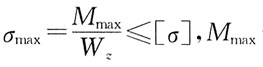 越小σmax越小,梁就越安全。题述四个弯矩图中显然选项d)图Mmax最小。
越小σmax越小,梁就越安全。题述四个弯矩图中显然选项d)图Mmax最小。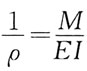 与弯矩成正比,故曲率的最大值发生在弯矩最大的截面上。
与弯矩成正比,故曲率的最大值发生在弯矩最大的截面上。
 计算中,σ的正负号不同,σ1的数值也不相同。
计算中,σ的正负号不同,σ1的数值也不相同。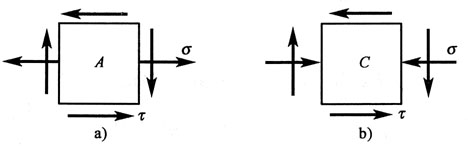
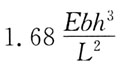
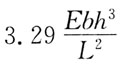

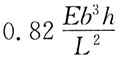
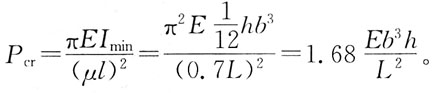
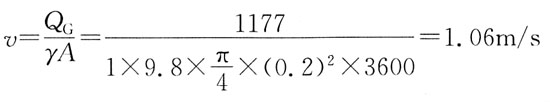
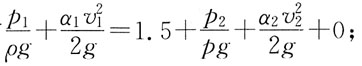
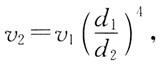 代入上式中,并代入题设数据。
代入上式中,并代入题设数据。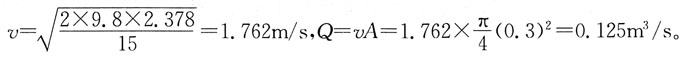

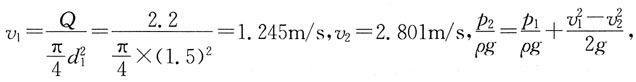 所以
所以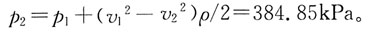
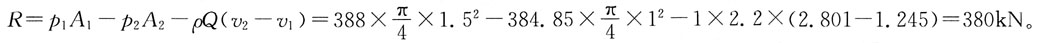
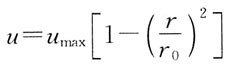
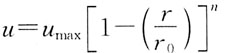
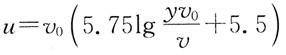

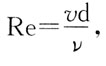 由此求出流速v,而流量
由此求出流速v,而流量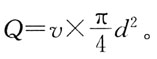
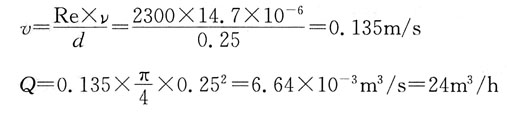
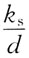 有关
有关 有关
有关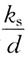 有关)。
有关)。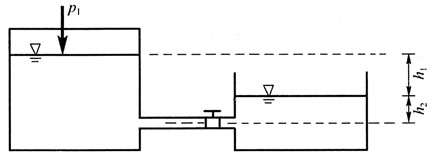
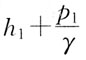
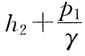
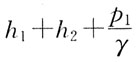
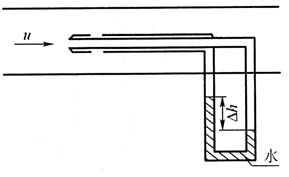
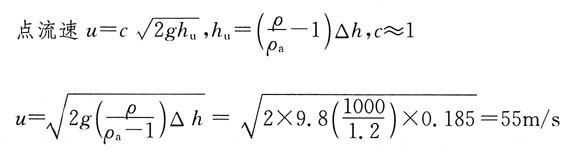




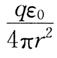
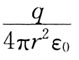
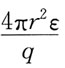
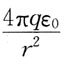
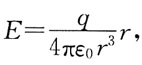 取绝对值
取绝对值