一、选择题2. 若3sinα+cosα=0，则
的值为______．
A．
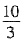
B．
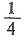
C．
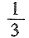
D．-2
A B C D
A
[解析] ∵3sinα+cosα=0，∴
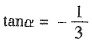
从而
．
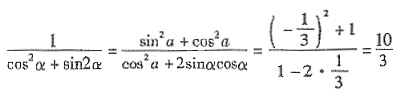
4. 若直线l
1：(a-1)y+(a+1)x=3与直线l
2：3ay=ax+1互相垂直，则a的值为______．
A B C D
C
[解析] 由题，直线l
1与直线l
2互相垂直，因此a≠-1，直线l
1的斜率为
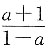
，直线l
2的斜率为
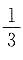
，因为两条直线相互垂直时，斜率的乘积为-1，所以
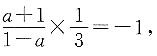
解得a=2．
5. 分段函数
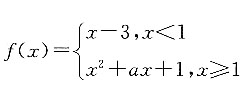
的值域为R，则a的值可能是______．
A B C D
D
[解析] x＜1时，函数的值域为(-∞，-2)；x≥1时，
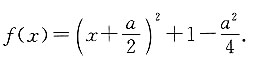
分两种情况进行讨论：①当a＞0时，
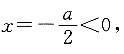
即f(x)的对称轴在x轴的负半轴，此时当x=1时，f(x)有最小值，因为函数的值域为R，故应有f(1)=1+a+1≤-2，得a≤-4，故此时a无解；②当a＜0时，
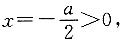
此时
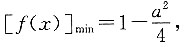
因为值域为R，所以
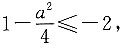
解得
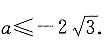
四个选项中只有D项符合条件．
7. 如图，函数y=2x和y=ax+4的图象相交于点A(m，3)，则不等式2x＜ax+4的解集为______
A．
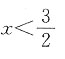
B．x＜3
C．
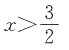
D．x＞3
A B C D
A
[解析] 把点A(m，3)代入y=2x中得
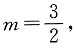
由图可知，当2x＜ax+4时，
故选A．
8. 函数y=f(2x-1)的定义域为(0，3)，则f(x
2+1)的定义域为______．
A．(1，5)
B．
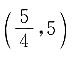
C．(1，10)
D．
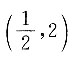
A B C D
B
[解析] y=f(2x-1)的定义域为(0，3)，即0＜2x-1＜3，解得
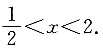
则
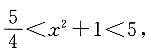
即f(x
2+1)的定义域为
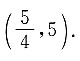
9. 设曲线
在点
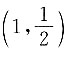
处的切线与直线ax+5y+1=0垂直，则a=______．
A．4
B．-4
C．
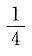
D．
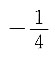
A B C D
A
[解析]
是曲线
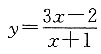
上的点，又因为
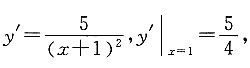
故在点
处切线的斜率为
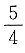
，又因为切线与直线ax+5y+1=0垂直，即
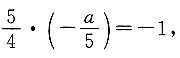
解得a=4．
10. 方程x
2-20x+16=0有两个不相等的实数根，若这两根是等差数列中的两项，则其等差中项是______，若这两根是等比数列中的两项，则其等比中项是______．
A B C D
D
[解析] 已知方程为x
2-20x+16=0，则x
1+x
2=20，x
1x
2=16．若x
1、x
2为等差数列中的两项，则其等差中项为
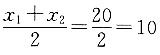
；若x
1、x
2为等比数列中的两项，则其等比中项为
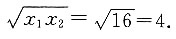
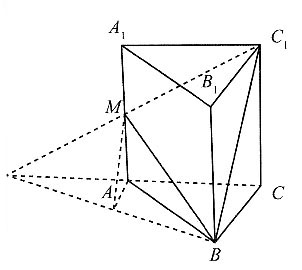
二、填空题1. 如图所示的直三棱柱，AB⊥BC，MA=MA
1=AB=BC=1，则面MBC
1与底面ABC的夹角的正切值为______．
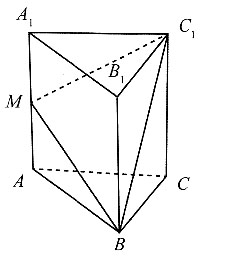
[解析] 延长C
1M与CA，交于N点，连接BN，则BN即为面MBC
1与底面ABC的的交线．过A点作AD⊥DN，连接MD．因为三棱柱为直三棱柱，所以MA⊥面ABC，又
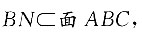
所以MA⊥BN，又MA∩AD=A，所以BN⊥面MDA，即BN⊥MD，所以∠MDA即面ABC与面MBC
1的二面角，根据余弦定理求得．
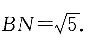
因为
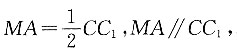
所以
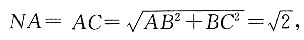
因为AB=BC=1，BC⊥AB，所以
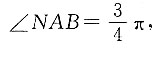
在
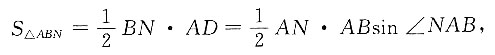
即
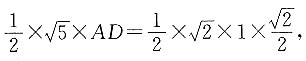
求得
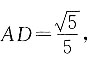
以两平面夹角的正切值
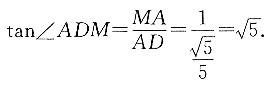
2. 函数(1+x)ln(1-2x)在x=0处的x的幂级数展开式为______．
[解析] 因为
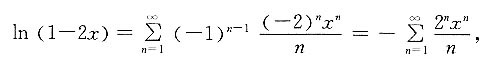
则
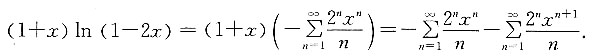
3. 若向量
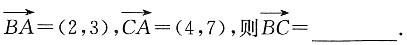
(-2，-4)
[解析]
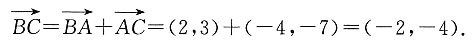
4. 已知平面直角坐标系中有点A(2，1)，过A点且与两坐标轴都相切的圆的方程为______．
(x-1)2+(y-1)2=1或(x-5)2+(x-5)2=25
[解析] 已知圆经过点A(2，1)，且与两坐标轴相切，则可知此圆一定在第一象限，圆心到两坐标轴的距离均为其半径长．设其半径为r，则圆的方程为(x-r)2+(y-r)2=r2．将点A的坐标代入，可得(2-r)2+(1-r)2=r2，化简可得r2-6r+5=0，解得r=1或5．故圆的方程为(x-1)2+(y-1)2=1或(x-5)2+(x-5)2=25．
5. 定义集合运算：A·B={Z|Z=xy，x∈A，y∈B}，设集合A={-2，0，1}，集合B={tanα，sinα}
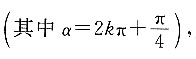
则集合A·B的所有元素之和为______．
[解析] 依题意可知，集合
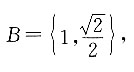
因为A·B={Z|Z=xy，x∈A，y∈B}，集合A={-2，0，1}，所以
所有元素之和为
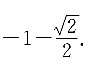
三、解答题在正方形ABCD中，边长为4cm，点P从B点向C点运动，点Q从C点向D点运动．点P运动的速度是点Q运动速度的2倍．P点运动的速度为1cm/s，△PCQ的面积为y．
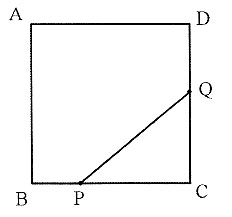
1. 求时间t与y的函数关系；
根据图象可知，
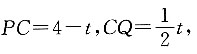
所以
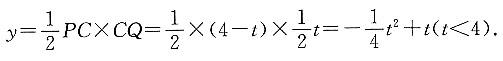
2. 哪一时刻△PCQ的面积最大，最大值为多少?
因为
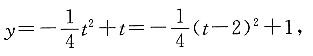
故当t=2时，y取最大值，即△PCQ的面积最大为1cm
2．
所以当t=2时，△PCQ的面积最大，为1cm
2．
3. 甲盒内有5个白球和3个黑球，从中任取3个球放入空盒乙中，然后从乙盒内任取2个球放入空盒丙中，最后从丙盒内再任取一个球，试求从丙盒内取出的球是黑球的概率．
丙盒中取出黑球的可能情况有4种：
①乙盒中为3个黑球，丙盒中为2个黑球
②乙盒中为2个黑球1个白球，丙盒中为2个黑球
③乙盒中为2个黑球1个白球，丙盒中为1个黑球1个白球
④乙盒中为1个黑球2个白球，丙盒中为1个黑球1个白球．
所以
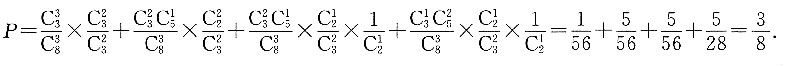
4. 若
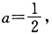
求f(x)的单调区间；
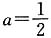
时，
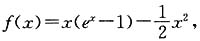
f'(x)=e
x-1+xe
x-x=(e
x-1)(x+1)．
当x∈(-∞，-1)时f'(x)＞0；当x∈(-1，0)时，f'(x)＜0；当x∈(0，+∞)时，f'(x)＞0．
故f(x)在(-∞，-1)，(0，+∞)单调递增，在(-1，0)单调递减。
5. 若当x≥0时f(x)≥0，求a的取值范围．
f(x)=x(xa-1-ax)．令g(x)=xa-1-ax，则g'(x)=ex-a．
若a≤1，则当x∈(0，+∞)时，g'(x)＞0，g(x)为减函数，而g(0)=0，从而当x≥0时g(x)≥0，即f(x)≥0．
若a＞1，则当x∈(0，lna)时，g'(x)＜0，g(x)为减函数，而g(0)=0，从而当x∈(0，lna)时g(x)＜0，即f(x)＜0．
综合得a的取值范围为(-∞，1]．
6. 已知复数
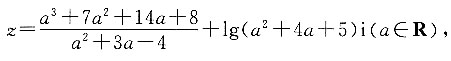
求是否存在实数a使复数z为实数，如果存在，求出该实数；如果不存在，请说明理由．
存在实数a使复数z为实数．
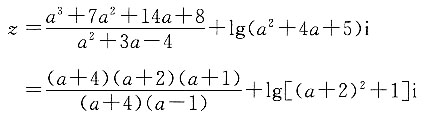
当z为实数时，
应满足
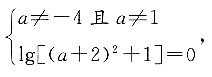
即(a+2)
2+1=1，
解得a=-2，
此时z=0．
则求：7. 此数列的通项公式a
n；
因为
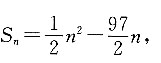
则当n=1时，
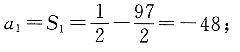
当n≥2时，
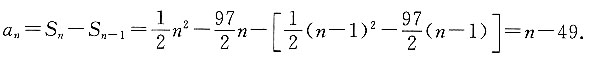
又n=1也符合a
n=n-49，
则此数列的通项公式a
n=n-49，即数列{a
n}是以-48为首项，公差为1的等差数列．
8. a
2+a
4+a
6+…+a
94+a
96+a
98的值．
由第一小题可知，偶数项是首项为a
2=-47，公差为2的等差数列，则a
2+a
4+a
6+…+a
94+a
96+a
98=T
49，
所以四边形MBNO为平行四边形，ON//BM．ON交面PDC于O点，因为
所以ON与PC为异面直线，即BM与PC为异面直线．
的二项展开式中，x的系数为______
所以x的系数为-40，选D．
深色：已答题 浅色：未答题