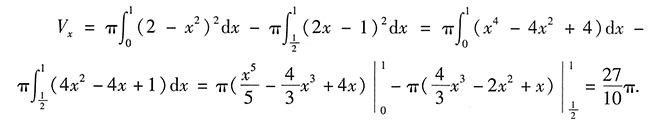第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中，只有一项是符合题目要求的)1. 设函数f(x)=
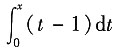
，则f(x)有______．
A．极大值
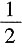
B．极大值
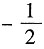
C．极小值
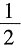
D．极小值
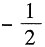
A B C D
D
[解析] f'(x)=x-1，f"(x)=1＞0，所以f(x)有极小值f(1)=
=
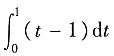
，所以选D．
2. 已知
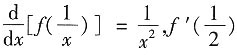
等于______．
A．-2
B．-1
C．
D．1
A B C D
B
[解析] 因为
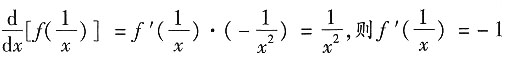
．当x=2时，得
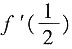
=-1，故选B．
3. 设函数y=f(x)在点(x，f(x))处的切线斜率为
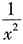
，则过点(1，0)的切线方程为______．
A．y=x+1
B．y=x-1
C．
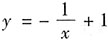
D．
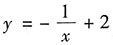
A B C D
B
[解析] 函数y=f(x)在点(x，f(x))处导数的几何意义是表示该函数对应曲线过点(x，f(x))的切线的斜率．由
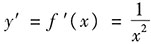
，得y'(1)=1．且过点(1，0)，则y=x-1．
5. 函数f(x)=
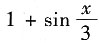
在点x=0处的导数是______．
A．0
B．
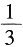
C．
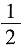
D．3
A B C D
B
[解析] 因为f'(x)=
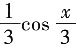
，所以f'(0)=
．
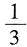
6. 函数y=f(x)有f'(x
0)=
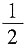
，当Δx→0时，函数在x=x
0处的微分dy等于______．
A．2dx
B．
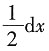
C．dx
D．0
A B C D
B
[解析] 因为dy=y'fx=
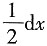
，故选B．
7. 反常积分
等于______．
A．1
B．
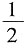
C．
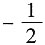
D．+∞
A B C D
D
[解析]
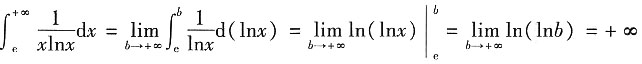
，所以反常积分是发散的，选D．
8. 设f(x)为连续函数，则
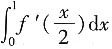
等于______．
A．
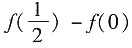
B．
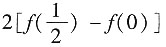
C．
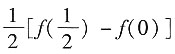
D．f(2)-f(0)
A B C D
B
[解析]
=
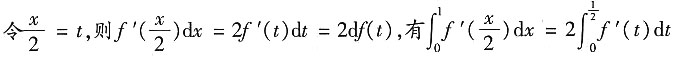
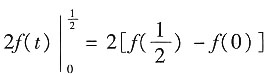
，所以选B．
9. 设
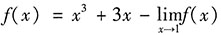
，则f(x)等于______．
- A.x3+3x-4
- B.x3+3x-3
- C.x3+3x-2
- D.x3+3x-1
A B C D
C
[解析] 设
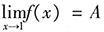
，对等式两边取得极限：
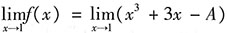
，则f(x)=x
3+3x-A，即A=4-A．得A=2，所以f(x)=x
3+3x-2，选C．
10. 已知f(x)=e
-2x+
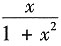
，则
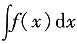
等于______．
A．-e
-2x+arctanx+C
B．
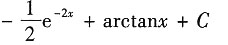
C．
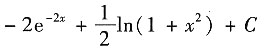
D．
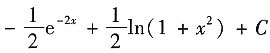
A B C D
D
[解析] 因为f(x)=
+
．
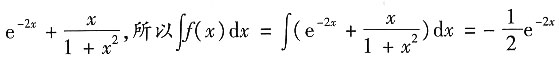
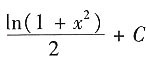
第Ⅱ卷(非选择题)
二、填空题1. 已知y=xe
-2x，则y"=______．
4(x-1)e-2x
[解析] y'=e-2x-2xe-2x=(1-2x)e-2x，y"=-2e-2x-2(1-2x)e-2x=4(x-1)e-2x．
2. 函数y=x-ln(1+x)的驻点为x=______．
0
[解析] 根据定义，使f'(x)=0的点称为函数f(x)的驻点．因此有y'=1-
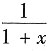
=0，得x=0．
3. 设函数y=ln(1+x
2)，则dy=______．
[解析] 因为
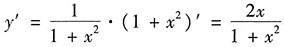
，所以
．
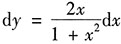
4. 曲线y=xlnx-x在x=e处的法线方程为______．
x+y-e=0
[解析] 因为y'=lnx+1-1=lnx，y'|
x=e=1=k
切线，则法线斜率
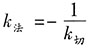
，得k
法=-1．当x=e时，y=0，所以法线方程为y=-(x-e)，即x+y-e=0．
5. 设f(x)的n-1阶导数为
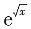
，则f
(n)(x)=______．
[解析]
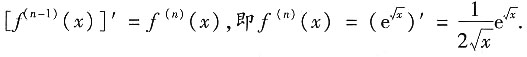
6. 由曲线y=x和y=x
2围成的平面图形的面积S=______．
[解析] 画出平面图形如图阴影部分所示，则
．
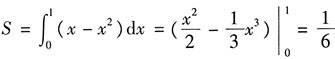
7. 设函数f(x)=lnx，则
=______．
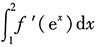
8. 设
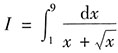
，若用
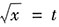
换成对t的积分再求解，可解得I=______．
2ln2
[解析] 令
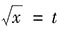
，则x=t
2，dx=2tdt．当x=1时，t=1；x=9时，t=3．因此
．
9. 已知z=f(xy，x
2)，且
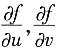
都存在，则dz=______．
[解析] 因为
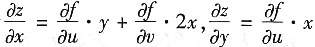
，所以dz=
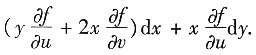
10. 设f(x)=e
x，g(x)=x
3，则
=______．
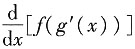
e3x2·6x
[解析] 因为g'(x)=3x
2,即f[g'(x)]=
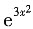
，所以
．
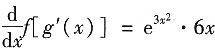
三、解答题(本题共70分．解答应写出推理、演算步骤)1. 设z=z(x，y)由方程
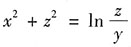
确定，求dz．
解：对等式两边求微分得
，
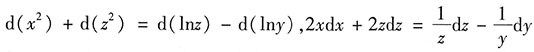
所以
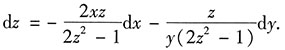
3. 设f"存在，
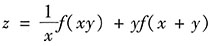
，求
．
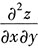
4. 设函数
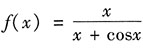
，求f'(x)．
解：
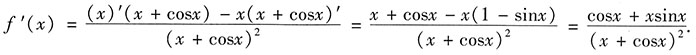
5. 计算
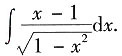
解：
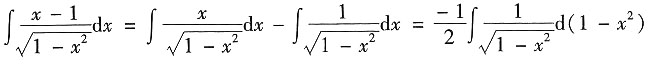
-arcsinx=-
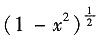
-arcsinx+C．
6. 设y=ln[cos(2x+1)]，求dy．
解：
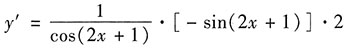
，所以dy=-22tan(2x+1)dx．
7. 设函数
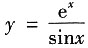
，求dy．
解：因为
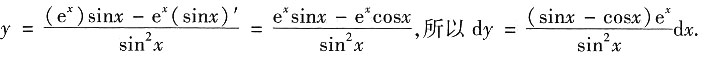
8. 求由曲线y=2-x
2，y=2x-1及x≥0围成的平面图形的面积S以及此平面图形绕x轴旋转一周所得旋转体的体积V
x．
解：由已知曲线画出平面图形为如图所示的阴影区域．
由
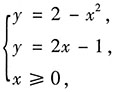
得交点坐标为(1，1)，则
，
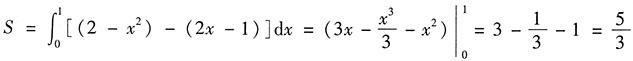
，则f'(1)=1，选C．
，则
，所以
．
后直接得
，则有
深色：已答题 浅色：未答题