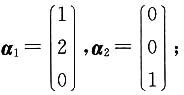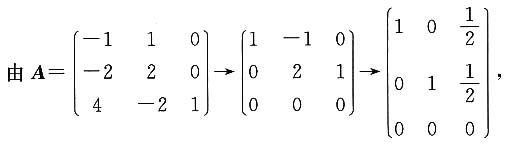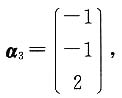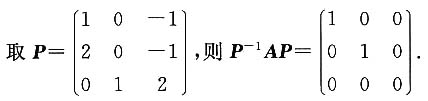一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的)1.
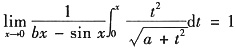
. 则常数a,b的值为______
- A.a=4,b=1
- B.a=-4,b=1
- C.a=4,b=-1
- D.a=-4,b=-1
A B C D
A
[考点] 求极限中的参数
[解析] 由
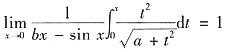
知
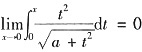
.
故
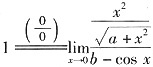
,于是
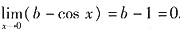
.
故b=1,而
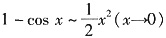
.
于是
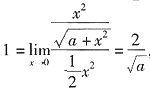
,故a=4. 即有
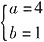
. 选A.
3. 设常数k>0,函数
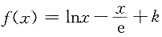
在(0,+∞)内的零点个数为
A B C D
B
[解析] 因为f(0
+)=-∞,又
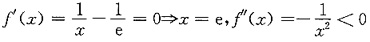
所以f(e)=k>0为极大值,且
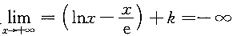
,
于是f(x)在(0,e)和(e,+∞)上分别恰有一个零点,故选(B).
4. 设A=(α
1,α
2,α
3,α
4)是4阶矩阵,A
*为A的伴随矩阵.若(1,0,1,0)
T是方程组Ax=0的一个基础解系,则A
*x=0的基础解系可为______
- A.α1,α3.
- B.α1,α2.
- C.α1,α2,α3.
- D.α2,α3,α4.
A B C D
D
[解析] 首先,4元齐次线性方程组A*x=0的基础解系所含解向量的个数为4-r(A*),其中r(A*)为A*的秩,因此求r(A*)是一个关键.其次,由Ax=0的基础解系只含1个向量,即4-r(A)=1,得r(A)=3,于是由r(A*)与r(A)的关系,知r(A*)=1,因此,方程组A*x=0的基础解系所含解向量的个数为4-r(A*)=3,故选项A、B不对.再次,由(1,0,1,0)T是方程组Ax=0或x1α1+x2α2+x3α3+x4α4=0的解,知α1+α3=0,故α1与α3线性相关,于是只有选项D正确.
本题综合考查基础解系、伴随矩阵、矩阵的秩、线性方程组的向量形式及向量组的线性相关性等基本概念.其中,n元齐次线性方程组Ax=0的基础解系所含解向量的个数(即Ax=0的解空间的维数)为n-r(A),以及r(A)与r(A*)的关系等概念,已考过多次,属于线性代数中很基本也很重要的一些结论,应该深刻理解.
5. 位于两圆x
2+y
2=2y与x
2+y
2=4y之间的质量分布均匀的薄板重心坐标是______
A.
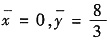
B.
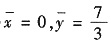
C.
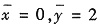
D.
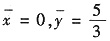
A B C D
B
[考点] 平面上均匀薄板重心的坐标
[解析] 薄板占有的平面区域为
D={(x,y)|2y≤x
2+y
2≤4y}
={(r,θ)|0≤θ≤π,2sin θ≤r≤4sin θ}.
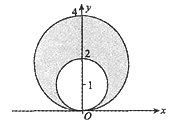
不妨设面密度μ=1,则
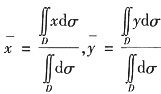
.
D关于x=0(y轴)对称,故
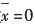
;
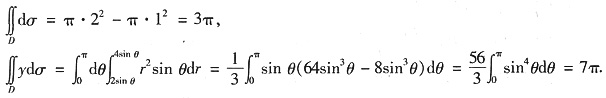
于是
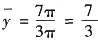
. 从而重心的坐标为
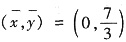
. 选B.
7. 设f(x)在(-∞,+∞)内有定义,且
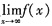
=a,g(x)=
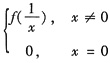
,则______
- A.x=0必是g(x)的第一类间断点.
- B.x=0必是g(x)的第二类间断点.
- C.x=0必是g(x)的连续点.
- D.g(x)在点x=0处的连续性与a的取值有关.
A B C D
D
[解析] 因为
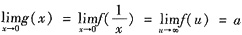
(令u=
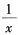
),又g(0)=0,故
当a=0时,
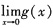
=g(0),即g(x)在点x=0处连续;
当a≠0时,
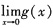
≠g(0),即x=0是g(x)的第一类间断点.
因此,g(x)在点x=0处的连续性与a的取值有关,故选D.
8. 已知级数
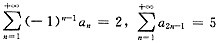
,则级数
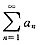
等于______
A B C D
C
[解析] 由于
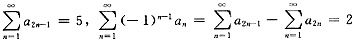
,
则
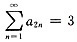
.又
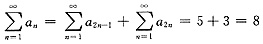
本题主要考查常数项级数的定义和性质.
9. 设f
1(x)为标准正态分布的概率密度,f
2(x)为[-1,3]上均匀分布的概率密度,若
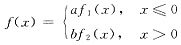
,(a>0,b>0)
为概率密度,则a,b应满足______
- A.2a+3b=4.
- B.3a+2b=4.
- C.a+b=1.
- D.a+b=2.
A B C D
A
[解析] 由题意知:
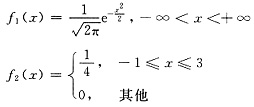
故:
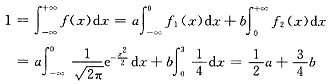
所以2a+3b=4,故选A.
解中
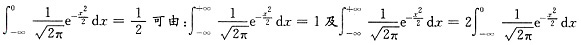
=
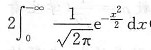
(注意
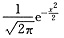
是偶函数且
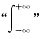
为对称的积分区间)得到,也可由:设随机变量X~N(0,1),X的概率密度即为f
1(x),则
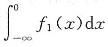
=P(X≤0)=Φ(0)=
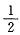
得到,这要求学生对正态分布的概率计算较熟悉.本题主要考查概率密度的性质:
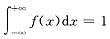
.当然,本题中的几个随机变量(题目及解符号中甚至连随机变量的记号都不用出现)并无明显的函数关系,勿出现“
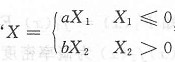
”一类莫名其妙的式子,也勿有
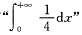
一类荒唐的式子.
二、填空题1. 设
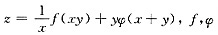
具有二阶连续导数,则
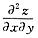
=______.
[解析] 由复合函数求导法知
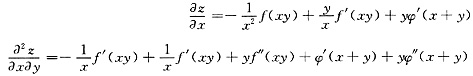
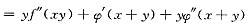
本题主要考查复合函数求导法.
2.
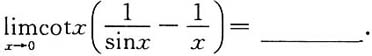
3.
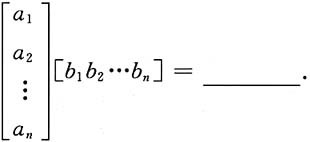
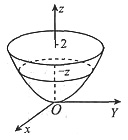
4. 设Ω由曲面∑:z=x
2+y
2(0≤z≤2)与平面z=2围成,f(z)是连续函数,三重积分
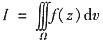
可表示成定积分为______.
[考点] 将三重积分化为定积分
[解析] 过z∈(0,2)作平行于xOy的平面,截得Ω的平面区域记为D(z),用柱坐标计算,有
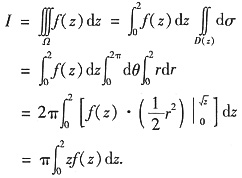
5. 设A=(a
ij)
3×3是实正交矩阵,且a
11=1,b=(1,0,0)
T,则线性方程组Ax=b的解是______.
[解析] 由于正交矩阵的行(列)向量组均为正交单位向量组,故
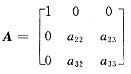
,又A
-1=A
T,故方程组Ax=b的解为x=A
-1b=A
Tb=

.
6. 若函数
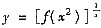
,其中f是可微的正值函数,则dy=______.
[解析] 由于函数可写为
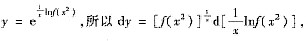
故
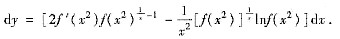
三、解答题本题共70分,解答应写出文字说明、证明过程或演算步骤.1. 设总体X的概率分布为
| X | 0 | 1 | 2 | 3 |
| p | θ2 | 2θ(1-θ) | θ2 | 1-2θ |
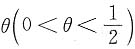
是未知参数.用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值.
解:E(X)=0×θ
2+1×2θ(1-θ)+2×θ
2+3×(1-2θ)=3-4θ,
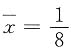
(3+1+3+0+3+1+2+3)=2,令

得参数θ的矩估计值为
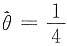
.
L(θ)=θ
2×[2θ(1-θ)]
2×θ
2×(1-2θ)
4=4θ
6(1-θ)
2(1-2θ)
4,
lnL(θ)=ln4+6lnθ+2ln(1-θ)+4ln(1-2θ),
令
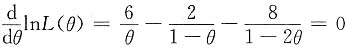
得参数θ的最大似然估计值为
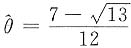
.
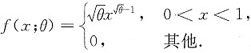 X1,X2,…,Xn为粗总体X的简单随机样本.
X1,X2,…,Xn为粗总体X的简单随机样本.2. 求未知参数θ的最大似然估计量;
解:总体X是连续型随机变量,其似然函数为
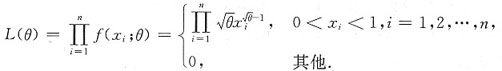
当0<x
i<1(i=1,2,…,n)时,L(θ)>0,取对数得

求导并令其等于0,得
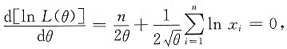
解得
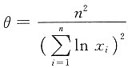
,则θ的最大似然估计量为
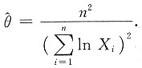
4. 设u=f(x,y)满足du=y
2dx+(2xy+1)dy,且f(0,0)=1,计算
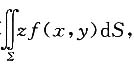
其中∑是
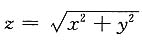
被x
2+(y-1)
2=1所截的部分.
解:由du=y
2dx+(2xy+1)dy=y
2dx+2xydy+dy=d(xy
2+y)得
f(x,y)=xy
2+y+C,
由f(0,0)=1得C=1,从而f(x,y)=xy
2+y+1.

5. 若f'(x)在[0,2π]上连续,且f'(x)≥0,则对任意正整数n,有
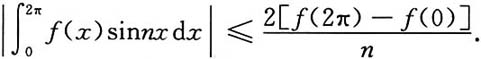
解:利用分部积分有
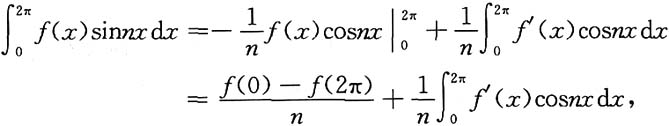
因为,f'(x)≥0,所以,f(2π)≥f(0),有

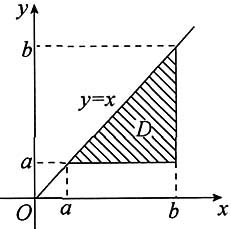
6. 设f(x)在[a,b]上连续,试证:
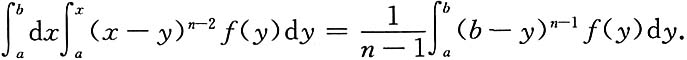
证:
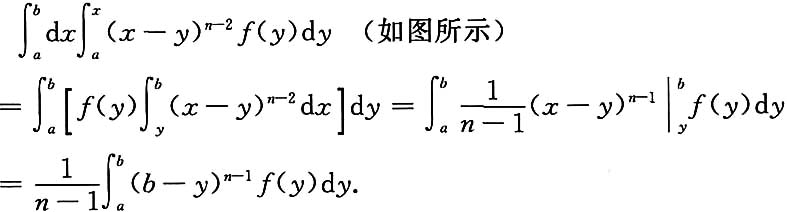
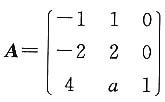 可对角化.
可对角化.7. 求常数a;
解:由|λE-A|=
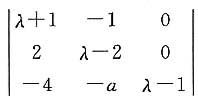
=λ(λ-1)
2=0得λ
1=λ
2=1,λ
3=0.
因为A可对角化,所以r(E-A)=1,
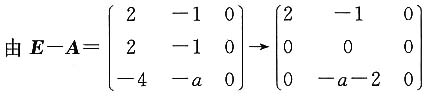
得a=-2.
8. 求可逆矩阵P,使得P
-1AP为对角矩阵.
解:将λ=1代入(λE-A)X=0中得(E-A)X=0
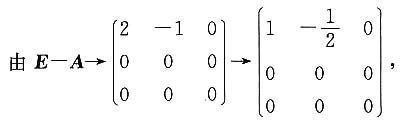
得λ=1对应的线性无关的特征向量为
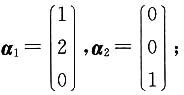
将λ=0代入(λE-A)X=0得AX=0,
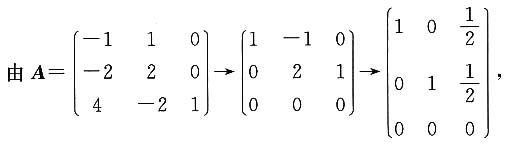
得λ=0对应的线性无关的特征向量为
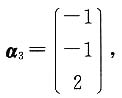
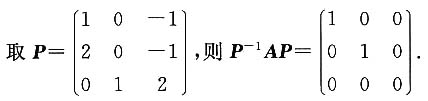
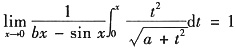 . 则常数a,b的值为______
. 则常数a,b的值为______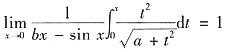 知
知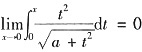 .
.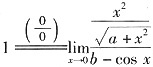 ,于是
,于是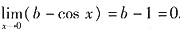 .
.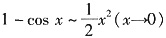 .
.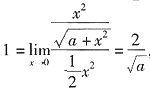 ,故a=4. 即有
,故a=4. 即有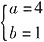 . 选A.
. 选A.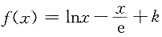 在(0,+∞)内的零点个数为
在(0,+∞)内的零点个数为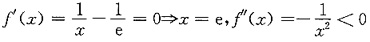
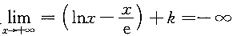 ,
,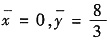
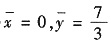
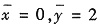
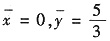

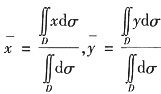 .
.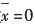 ;
;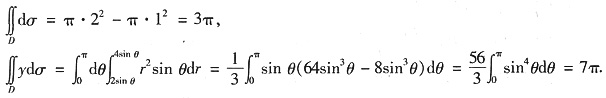
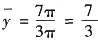 . 从而重心的坐标为
. 从而重心的坐标为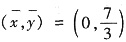 . 选B.
. 选B.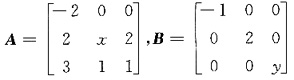
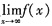 =a,g(x)=
=a,g(x)=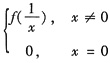 ,则______
,则______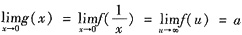 (令u=
(令u=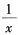 ),又g(0)=0,故
),又g(0)=0,故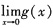 =g(0),即g(x)在点x=0处连续;
=g(0),即g(x)在点x=0处连续;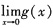 ≠g(0),即x=0是g(x)的第一类间断点.
≠g(0),即x=0是g(x)的第一类间断点.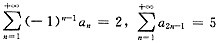 ,则级数
,则级数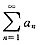 等于______
等于______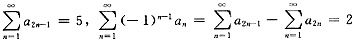 ,
,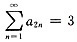 .又
.又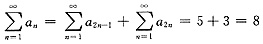
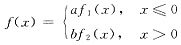 ,(a>0,b>0)
,(a>0,b>0)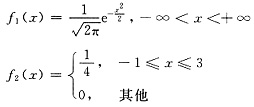
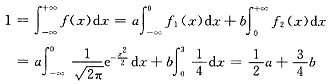
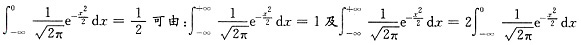 =
=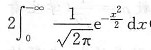 (注意
(注意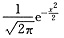 是偶函数且
是偶函数且 为对称的积分区间)得到,也可由:设随机变量X~N(0,1),X的概率密度即为f1(x),则
为对称的积分区间)得到,也可由:设随机变量X~N(0,1),X的概率密度即为f1(x),则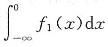 =P(X≤0)=Φ(0)=
=P(X≤0)=Φ(0)=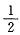 得到,这要求学生对正态分布的概率计算较熟悉.本题主要考查概率密度的性质:
得到,这要求学生对正态分布的概率计算较熟悉.本题主要考查概率密度的性质: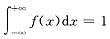 .当然,本题中的几个随机变量(题目及解符号中甚至连随机变量的记号都不用出现)并无明显的函数关系,勿出现“
.当然,本题中的几个随机变量(题目及解符号中甚至连随机变量的记号都不用出现)并无明显的函数关系,勿出现“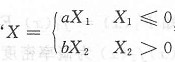 ”一类莫名其妙的式子,也勿有
”一类莫名其妙的式子,也勿有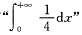 一类荒唐的式子.
一类荒唐的式子.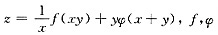 具有二阶连续导数,则
具有二阶连续导数,则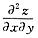 =______.
=______.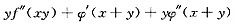
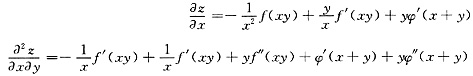
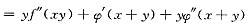
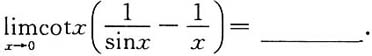
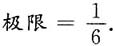
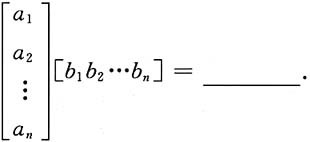

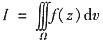 可表示成定积分为______.
可表示成定积分为______.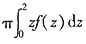
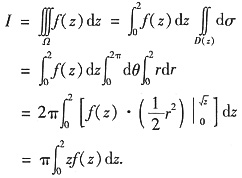


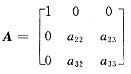 ,又A-1=AT,故方程组Ax=b的解为x=A-1b=ATb=
,又A-1=AT,故方程组Ax=b的解为x=A-1b=ATb= .
.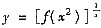 ,其中f是可微的正值函数,则dy=______.
,其中f是可微的正值函数,则dy=______.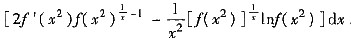
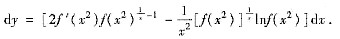
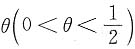 是未知参数.用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值.
是未知参数.用样本值3,1,3,0,3,1,2,3求θ的矩估计值和最大似然估计值.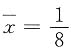 (3+1+3+0+3+1+2+3)=2,令
(3+1+3+0+3+1+2+3)=2,令 得参数θ的矩估计值为
得参数θ的矩估计值为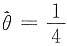 .
.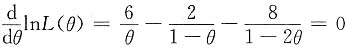 得参数θ的最大似然估计值为
得参数θ的最大似然估计值为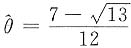 .
.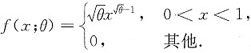 X1,X2,…,Xn为粗总体X的简单随机样本.
X1,X2,…,Xn为粗总体X的简单随机样本.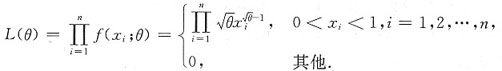

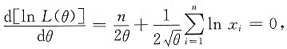
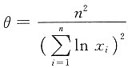 ,则θ的最大似然估计量为
,则θ的最大似然估计量为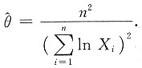
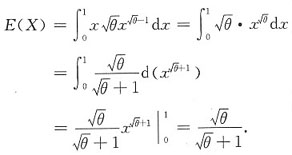
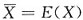 ,即
,即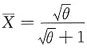 ,解得θ的矩估计量为
,解得θ的矩估计量为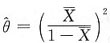 ,其中
,其中
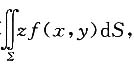 其中∑是
其中∑是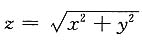 被x2+(y-1)2=1所截的部分.
被x2+(y-1)2=1所截的部分.
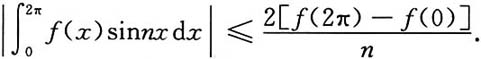
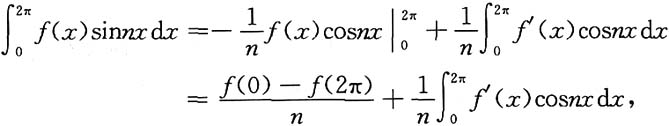

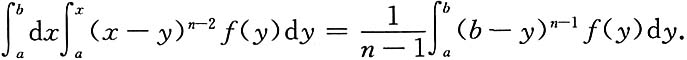
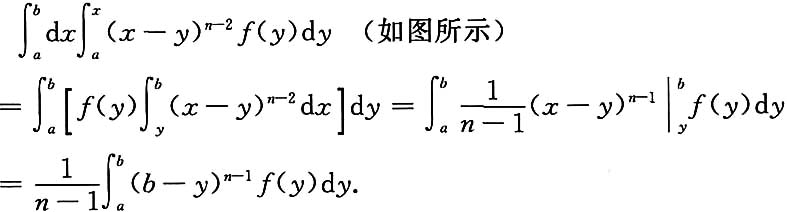
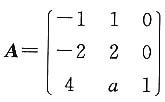 可对角化.
可对角化.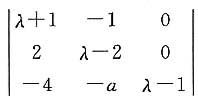 =λ(λ-1)2=0得λ1=λ2=1,λ3=0.
=λ(λ-1)2=0得λ1=λ2=1,λ3=0.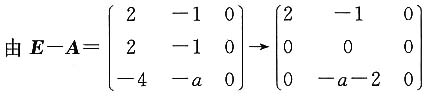 得a=-2.
得a=-2.