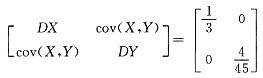一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的)1. 设随机变量X与Y相互独立,且分别服从参数为1与参数为4的指数分布,则P(X<Y)=______
A.
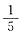
B.
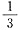
C.
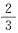
D.
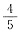
A B C D
A
[解析] 由题意,X,Y的概率密度分别为
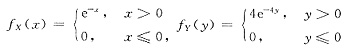
则(X,Y)的(联合)概率密度为
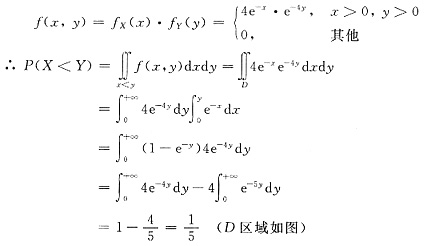

已知(X,Y)的(联合)概率密度时求概率是基本和常见的题.本题有x与y的独立性,所以由X,Y的(边缘)概率密度(几个特殊分布的概率密度要熟记噢)能确定(X,Y)的(联合)概率密度。累次积分用
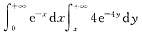
也可.建议
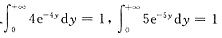
这种式子在考场上能一眼看出(因为这是由概率密度的性质得到的).又建议做题时不要出现
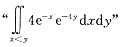
这种式子,X,Y的概率密度不要分别用f(x),f(y)表示(函数记号无区别)这种不妥当的式子.
2. 设随机变量X的密度函数为φ(x),且φ(-x)=φ(x),F(x)是x的分布函数.则对任意实数a,有______
A.
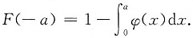
B.
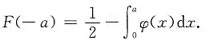
C.F(-a)=F(a).
D.F(-a)=2F(a)-1.
A B C D
B
[解析] 思路一:
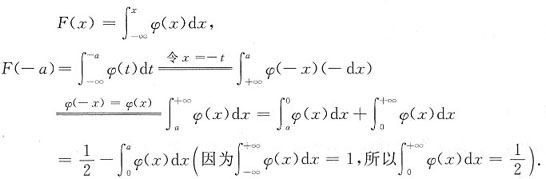
思路二:图像法(如下图)
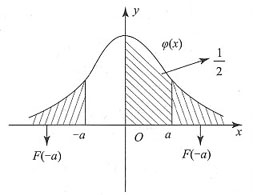
由图知

3. 由球面
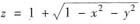
与锥面
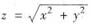
所围立体的体积等于______
A.
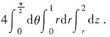
B.
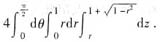
C.
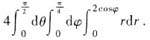
D.
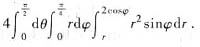
A B C D
B
[解析] 利用对称性可知,所同立体的体积V为在第一卦限部分的体积V
1的四倍.而第一卦限部分在xOy平面上的投影区域为D:x
2+y
2≤1,x≥0,y≥0,所以
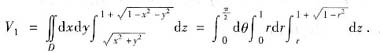
所以应选B.
5. 与矩阵
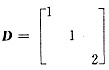
相似的矩阵是______
A.
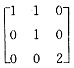
B.
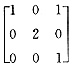
C.
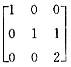
D.

A B C D
C
[解析] A与对角矩阵D相似
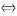
A的特征值为λ
1=λ
2=1,λ
3=2,且A的对应于2重特征值1的线性无关特征向量的个数为2。后一条件即方程组(E-A)x=0的基础解系含2个向量,即3-r(E-A)=2,或r(E-A)=1,经验证,只有备选项C中的矩阵满足上述要求.
6. 设λ
1,λ
2是矩阵A的两个不同的特征值,对应的特征向量分别为α
1,α
2,则α
1,A(α
1+α
2)线性无关的充分必要条件是______
A B C D
B
[解析] 解1 由λ
1≠λ
2及特征值的性质知α
1,α
2线性无关.显然,向量组{α
1,A(α
1+α
2)}={α
1,λ
1α
1+λ
2α
2}等价于向量组{α
1,λ
2α
2}.当λ
2≠0时,它线性无关,当λ
2=0时,它线性相关,故α
1,A(α
1+α
2)线性无关
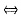
λ
2≠0.
解2 由条件知α
1,α
2线性无关,而
[α
1,A(α
1+α
2)]=[α
1,λ
1α
1+λ
2α
2]=
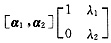
.
由于用列满秩矩阵左乘矩阵不改变矩阵的秩,得
α
1,A(α
1+α
2)线性无关
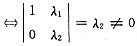
.
本题综合考查线性无关的概念及特征值的性质.
10. 设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=______
A B C D
B
[解析] ∵A与B独立,∴P(AB)=P(A)P(B).
故0.3=P(A-B)=P(A)-P(AB)=P(A)-P(A)P(B)
=P(A)[1-P(B)]=P(A)(1-0.5)=0.5(P(A)
得
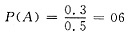
,
P(B-A)=P(B)-P(AB)=P(B)-P(A)P(B)=0.5-0.6×0.5=0.2
由A-B=A-AB及AB
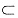
A,得P(A-B)=P(A-AB)=P(A)-P(AB),这是一个经常用到、要求学生用得很熟的Kq-(请勿出现“P(A-B)=P(A)-P(B)”一类式子)。在“无背景”的2个事件A,B的概率运算中,只要告诉你3个(不能互推的)等式条件,那么关于A,B的所有运算(并、交、差、补,包括条件概率)的概率,要求你都能熟练地求出,这是很基本的要求,在这种题上丢分实在太不应该了!
三、解答题本题共70分,解答应写出文字说明、证明过程或演算步骤.1. 设有微分方程y'+p(x)y=x
2,其中
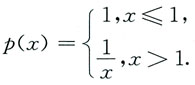
试求在(-∞,+∞)内的连续函数y=y(x),使之在(-∞,1)和(1,+∞)内都满足所给微分方程,且满足条件y(0)=2.
解:方法一 首先在区间(-∞,1]上求解初值问题:

不难得到方程的通解是
y=Ce
-x+x
2-2x+2,x≤1.
利用初始条件y(0)=2可确定C=0,从而所求的解为
y=x
2-2x+2,x≤1.
接着在区间(1,+∞)上求解方程
y'+p(x)y=x
2,x>1,
即
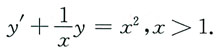
不难得到方程的通解是
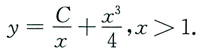
为得到符合题目要求的函数y=y(x),只需取C使得函数
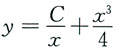
在x=1与函数y=x
2-2x+2连接起来,即
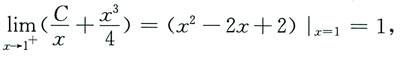
可得

也就是说分段函数
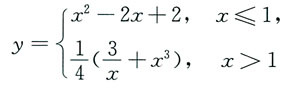
是符合题目要求的函数.
方法二 按照分段连续函数求原函数的方法,可设p(x)的一个原函数为
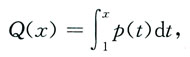
于是,当x≤1时,
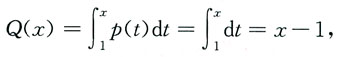
当x>1时,
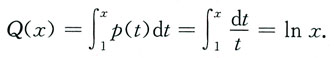
同理,可设x
2e
Q(x)的一个原函数为
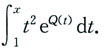
按照一阶线性微分方程通解公式可得方程y'+p(x)y=x
2的通解为
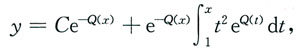
其中C是任意常数,下面来推导y的解析式.
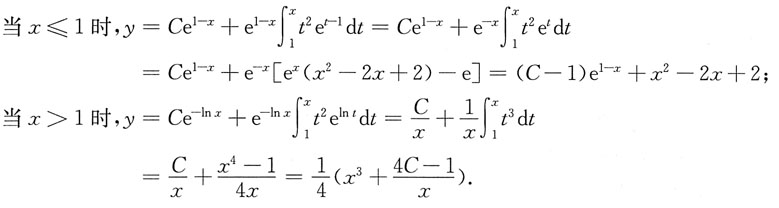
利用条件y(0)=2代入x≤1时y的表达式,可确定C=1,从而所求特解为
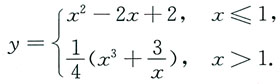
2. 接连不断且独立地对同一目标射击,直到命中为止,假设共进行n(n≥1)轮这样的射击,各轮射击的次数相应为k
1,k
2,…,k
n,试求命中率p的最大似然估计和矩估计.
解:P{X=k}=P(1-p)
k-1.
(Ⅰ)
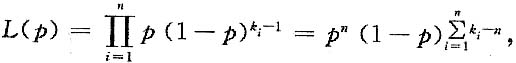
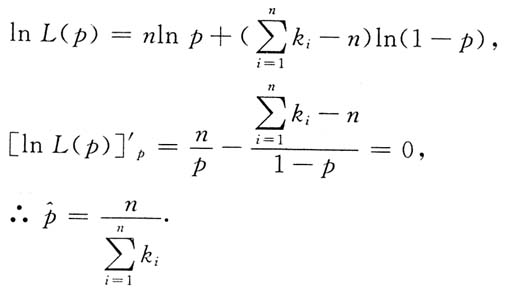
则
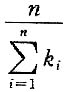
是p的极大似然估计.
(Ⅱ)求p的矩估计量.
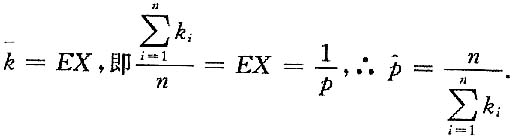
3. 已知当x→0时,
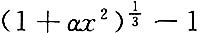
与cosx-1是等价无穷小,求常数α.
4. 求摆线的一拱与x轴所围图形的面积.
解:摆线的方程为
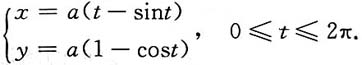
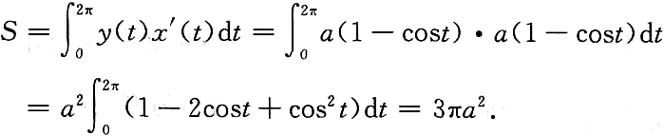
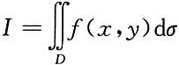 化为累次积分(两种形式),其中积分区域D给定如下:
化为累次积分(两种形式),其中积分区域D给定如下:5. D:由y
2=8x与x
2=y所围之区域;
解:
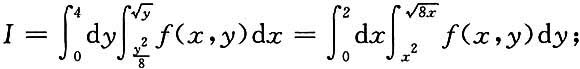
6. D:由x=3,x=5,x-2y+1=0及x-2y+7=0所围之区域;
解:
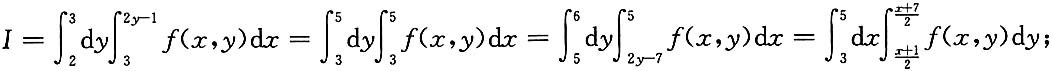
7. D:由x
2+y
2≤1,y≥x及x>0所围之区域;
解:
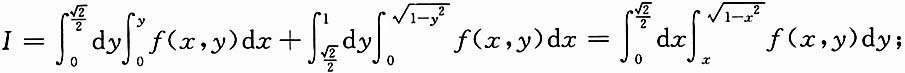
8. D:|x|+|y|≤1.
解:
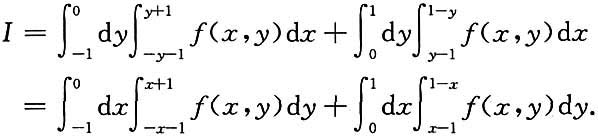
9. 设随机变量X在区间(-1,1)上服从均匀分布,Y=X
2,求(X,Y)的协方差矩阵和相关系数.
解:X的概率密度为:
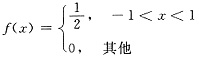
故EX=0,
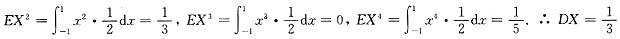
,
DY=E(Y
2)-(EY)
2=E(X
4)-EX
2)
2=
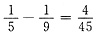
,cov(X,Y)=cov=(X,X
2)=E(X
3)-EX·EX
2=0,故知(X,Y)的相关系数ρ
(X,Y)=0,协方差阵为
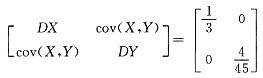
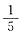
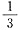
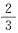
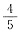
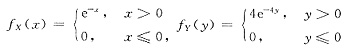
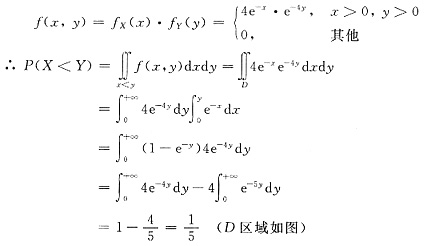

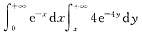 也可.建议
也可.建议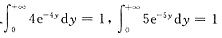 这种式子在考场上能一眼看出(因为这是由概率密度的性质得到的).又建议做题时不要出现
这种式子在考场上能一眼看出(因为这是由概率密度的性质得到的).又建议做题时不要出现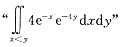 这种式子,X,Y的概率密度不要分别用f(x),f(y)表示(函数记号无区别)这种不妥当的式子.
这种式子,X,Y的概率密度不要分别用f(x),f(y)表示(函数记号无区别)这种不妥当的式子.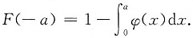
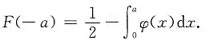
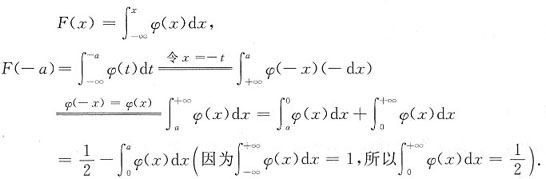


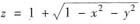 与锥面
与锥面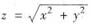 所围立体的体积等于______
所围立体的体积等于______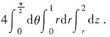
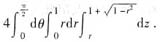
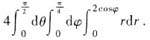
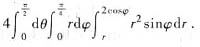
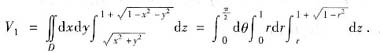
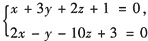 及平面∏:4x-2y+z-2=0,则直线L______
及平面∏:4x-2y+z-2=0,则直线L______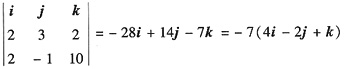 ,
,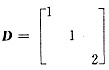 相似的矩阵是______
相似的矩阵是______



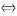 A的特征值为λ1=λ2=1,λ3=2,且A的对应于2重特征值1的线性无关特征向量的个数为2。后一条件即方程组(E-A)x=0的基础解系含2个向量,即3-r(E-A)=2,或r(E-A)=1,经验证,只有备选项C中的矩阵满足上述要求.
A的特征值为λ1=λ2=1,λ3=2,且A的对应于2重特征值1的线性无关特征向量的个数为2。后一条件即方程组(E-A)x=0的基础解系含2个向量,即3-r(E-A)=2,或r(E-A)=1,经验证,只有备选项C中的矩阵满足上述要求.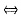 λ2≠0.
λ2≠0.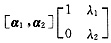 .
.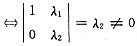 .
.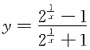 ,点x=0是______
,点x=0是______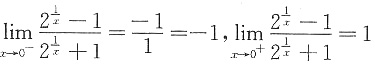 ,所以x=0为第一类跳跃间断点故选B.
,所以x=0为第一类跳跃间断点故选B.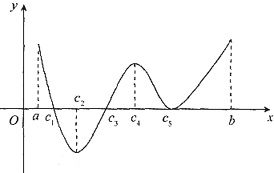
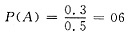 ,
, A,得P(A-B)=P(A-AB)=P(A)-P(AB),这是一个经常用到、要求学生用得很熟的Kq-(请勿出现“P(A-B)=P(A)-P(B)”一类式子)。在“无背景”的2个事件A,B的概率运算中,只要告诉你3个(不能互推的)等式条件,那么关于A,B的所有运算(并、交、差、补,包括条件概率)的概率,要求你都能熟练地求出,这是很基本的要求,在这种题上丢分实在太不应该了!
A,得P(A-B)=P(A-AB)=P(A)-P(AB),这是一个经常用到、要求学生用得很熟的Kq-(请勿出现“P(A-B)=P(A)-P(B)”一类式子)。在“无背景”的2个事件A,B的概率运算中,只要告诉你3个(不能互推的)等式条件,那么关于A,B的所有运算(并、交、差、补,包括条件概率)的概率,要求你都能熟练地求出,这是很基本的要求,在这种题上丢分实在太不应该了! 有特征向量
有特征向量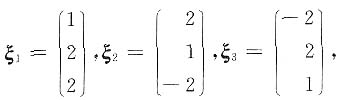 则|A|=______.
则|A|=______.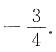
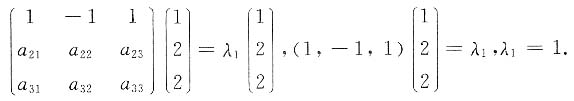

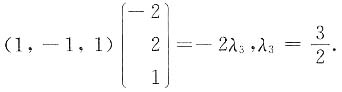
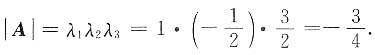
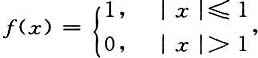 则f[f(x)]=______.
则f[f(x)]=______.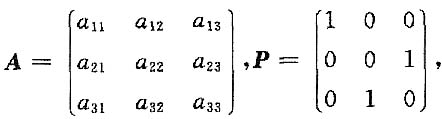 则P4AP5=______.
则P4AP5=______.
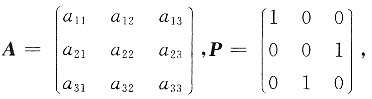
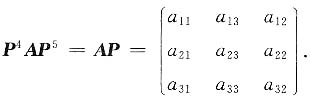
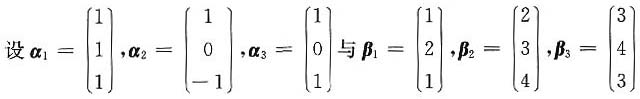 为三维空间的两组不同的基,令β=β1+2β2-3β3,则β在基α1,α2,α3下的坐标为______.
为三维空间的两组不同的基,令β=β1+2β2-3β3,则β在基α1,α2,α3下的坐标为______.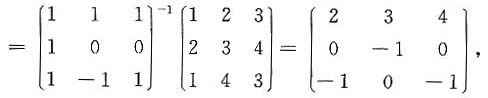
 =-4α1-2α2+2α3,
=-4α1-2α2+2α3,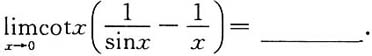
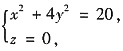 绕x轴旋转一周得到的旋转曲面在点
绕x轴旋转一周得到的旋转曲面在点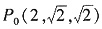 处指向外侧的单位法向量
处指向外侧的单位法向量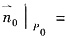 ______.
______.
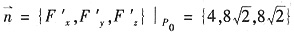 ,从而
,从而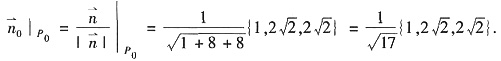
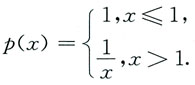

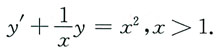
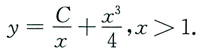
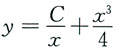 在x=1与函数y=x2-2x+2连接起来,即
在x=1与函数y=x2-2x+2连接起来,即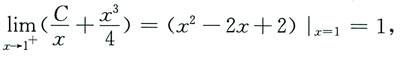
 也就是说分段函数
也就是说分段函数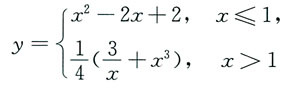
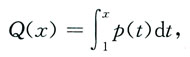
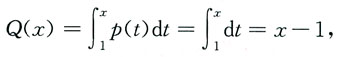
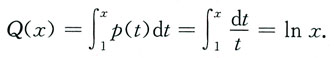
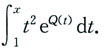
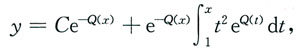
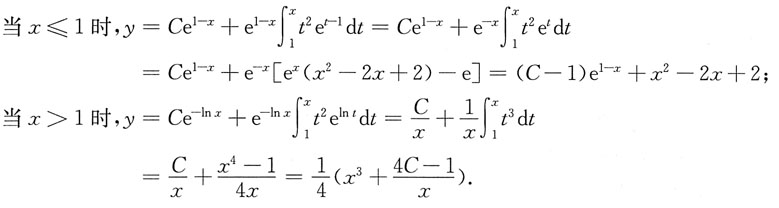
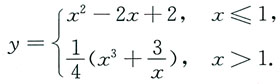
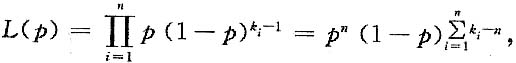
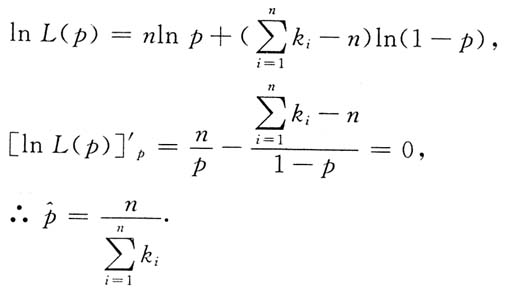
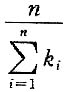 是p的极大似然估计.
是p的极大似然估计.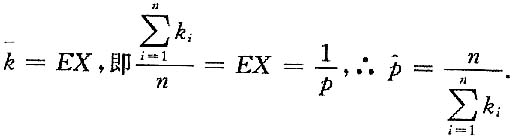
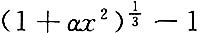 与cosx-1是等价无穷小,求常数α.
与cosx-1是等价无穷小,求常数α.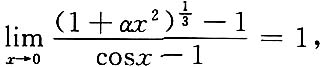
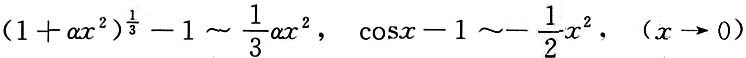
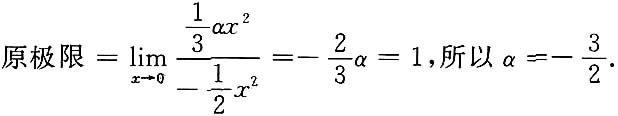
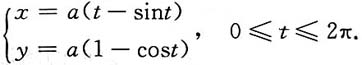
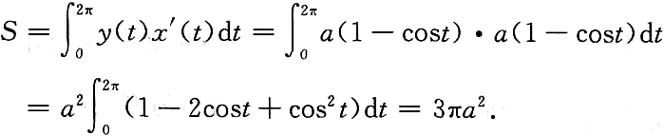
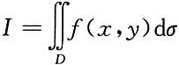 化为累次积分(两种形式),其中积分区域D给定如下:
化为累次积分(两种形式),其中积分区域D给定如下: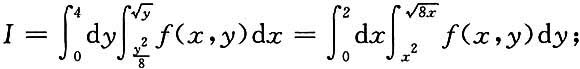
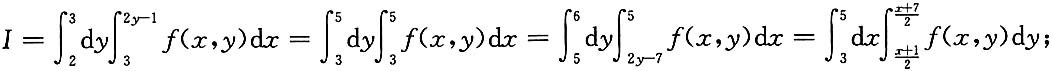
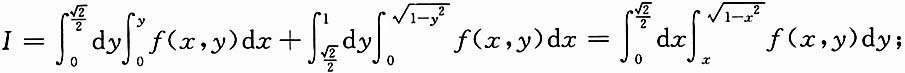
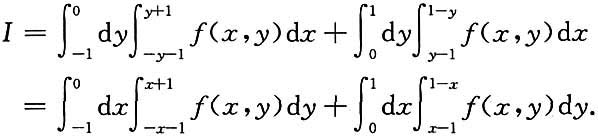
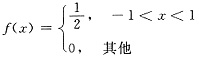
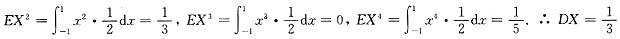 ,
,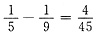 ,cov(X,Y)=cov=(X,X2)=E(X3)-EX·EX2=0,故知(X,Y)的相关系数ρ(X,Y)=0,协方差阵为
,cov(X,Y)=cov=(X,X2)=E(X3)-EX·EX2=0,故知(X,Y)的相关系数ρ(X,Y)=0,协方差阵为