银符考试题库B12
现在是:
试卷总分:150.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
 ,g(x)=
,g(x)=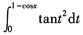 ,则x→0时,f(x)是g(x)的______
,则x→0时,f(x)是g(x)的______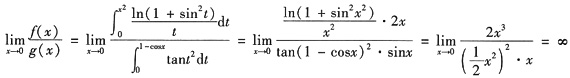 ,
,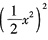 .
. 及平面π:4x-2y+z-2=0,则直线L______
及平面π:4x-2y+z-2=0,则直线L______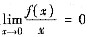 ,则______
,则______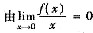 得f(0)=f'(0)=0.因此曲线y=f(x)在x=0处的切线方程为y=0,它就是x轴本身.所以C成立,D不成立.
得f(0)=f'(0)=0.因此曲线y=f(x)在x=0处的切线方程为y=0,它就是x轴本身.所以C成立,D不成立.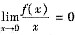 ,但f(0)不是极值,所以A,B不成立.因此应选C.
,但f(0)不是极值,所以A,B不成立.因此应选C.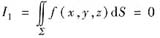
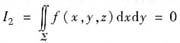
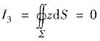
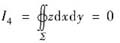
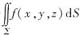 来说,是根据积分曲面∑的方程的形式来确定将∑向哪个坐标面投影的.如果∑的方程可写成z=z(x,y)的形式,则将∑向xOy面投影;如果∑的方程可写为y=y(x,z)(或x=x(y,z))的形式,则将∑向xOz面(或yOz面)投影.若∑的方程可同时表为几种不同的形式,则可选择其中最便于计算的投影方式(只讨论∑的方程为显式方程时曲面积分的计算方法,因此上面的讨论也限于显式方程的范围内).本题中,由于∑是柱面x2+y2=a2的一部分,它的方程不能写成z=z(x,y)的形式,故计算时不能将∑向xOy面投影.正确的做法是,将圆柱面∑分片向yOz面(或xOz面)投影.比如可将∑分为∑1和∑2两片,其中∑1:
来说,是根据积分曲面∑的方程的形式来确定将∑向哪个坐标面投影的.如果∑的方程可写成z=z(x,y)的形式,则将∑向xOy面投影;如果∑的方程可写为y=y(x,z)(或x=x(y,z))的形式,则将∑向xOz面(或yOz面)投影.若∑的方程可同时表为几种不同的形式,则可选择其中最便于计算的投影方式(只讨论∑的方程为显式方程时曲面积分的计算方法,因此上面的讨论也限于显式方程的范围内).本题中,由于∑是柱面x2+y2=a2的一部分,它的方程不能写成z=z(x,y)的形式,故计算时不能将∑向xOy面投影.正确的做法是,将圆柱面∑分片向yOz面(或xOz面)投影.比如可将∑分为∑1和∑2两片,其中∑1: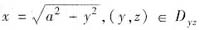 ;∑2:
;∑2: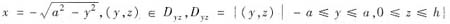 ,于是
,于是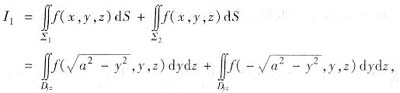
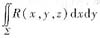 时,是将∑向xOy面投影;而计算
时,是将∑向xOy面投影;而计算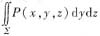 和
和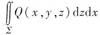 时,则将∑分别向yOz面和xOz面投影.本题中的积分I2是关于坐标x,y的第二类曲而积分,因此化为二重积分计算时,应将∑向xOy面投影.由于∑为柱面x2+y2=a2的一部分,它在xOy面上的投影是圆周,其面积是零,因此必有I2=0.故②正确.
时,则将∑分别向yOz面和xOz面投影.本题中的积分I2是关于坐标x,y的第二类曲而积分,因此化为二重积分计算时,应将∑向xOy面投影.由于∑为柱面x2+y2=a2的一部分,它在xOy面上的投影是圆周,其面积是零,因此必有I2=0.故②正确.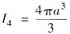 .
.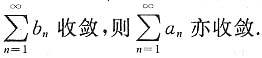
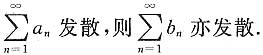
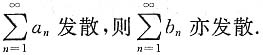
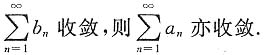
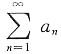 发散,从而
发散,从而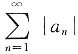 亦发散.因若后者收敛,则
亦发散.因若后者收敛,则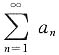 绝对收敛.又由|an|≤bn(n=1,2,…),故
绝对收敛.又由|an|≤bn(n=1,2,…),故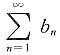 为正项级数,且
为正项级数,且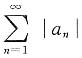 发散,由比较判别法知,
发散,由比较判别法知,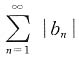 发散,选B.
发散,选B.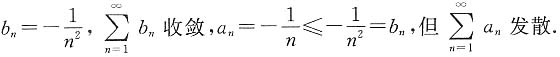
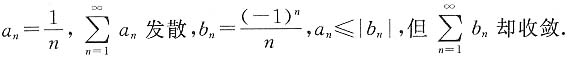

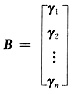 ,则AB=O的第i行为[ai1 ai2 … ain]
,则AB=O的第i行为[ai1 ai2 … ain]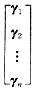 =ai1γ1+ai2γ2+…+ainγn=0,由此及A≠0也可推出B的行向量组线性相关.本题所用的关于乘积矩阵的按列(行)表示方法是一种重要方法,在讨论矩阵的秩、线性方程组及向量的有关问题中常常用到.
=ai1γ1+ai2γ2+…+ainγn=0,由此及A≠0也可推出B的行向量组线性相关.本题所用的关于乘积矩阵的按列(行)表示方法是一种重要方法,在讨论矩阵的秩、线性方程组及向量的有关问题中常常用到.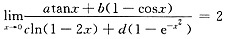 ,其中a2+c2≠0,则必有 ______
,其中a2+c2≠0,则必有 ______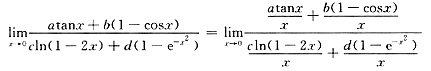

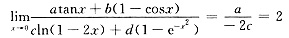
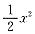 ,1-e-x2~x2,则分子和分母的最低阶无穷小项分别为atanx和cln(1-2x),它们都是x的一阶无穷小,则分子分母同除x问题很快得到解决.
,1-e-x2~x2,则分子和分母的最低阶无穷小项分别为atanx和cln(1-2x),它们都是x的一阶无穷小,则分子分母同除x问题很快得到解决.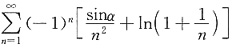 ,其中α为常数,则此级数______
,其中α为常数,则此级数______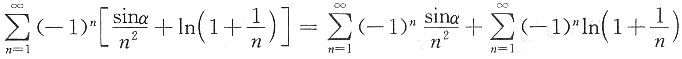 ,
,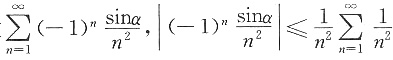 ,
,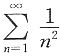 收敛,所以
收敛,所以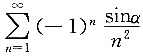 绝对收敛;
绝对收敛;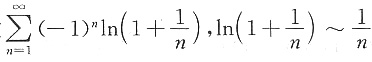 ,
,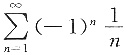 条件收敛,
条件收敛,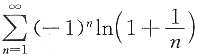 条件收敛.
条件收敛. 条件收敛,故选(B).
条件收敛,故选(B).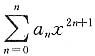 的收敛半径为4,则______.
的收敛半径为4,则______.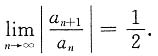
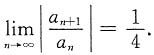
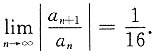
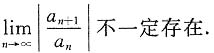
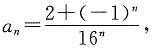 分别考虑两个幂级数
分别考虑两个幂级数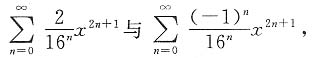
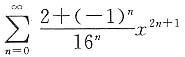

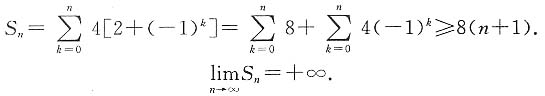
 不存在.所以选D.
不存在.所以选D.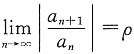 (ρ可以是+∞),则幂级数
(ρ可以是+∞),则幂级数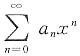 的收敛半径R可以由下面关系得到:当ρ=0时R=+∞;ρ=+∞时R=0;0<ρ<+∞时
的收敛半径R可以由下面关系得到:当ρ=0时R=+∞;ρ=+∞时R=0;0<ρ<+∞时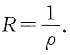 ”此定理的前提为an≠0,并且
”此定理的前提为an≠0,并且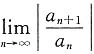 存在或为+∞.此两前提非常重要.①缺项的幂级数不能用这个办法计算,而应将该幂级数中的x看成“数”,用数项级数的办法考虑它的敛散性;②只知道幂级数的收敛半径,在并不知道
存在或为+∞.此两前提非常重要.①缺项的幂级数不能用这个办法计算,而应将该幂级数中的x看成“数”,用数项级数的办法考虑它的敛散性;②只知道幂级数的收敛半径,在并不知道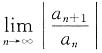 存在或为+∞的前提下,不能由收敛半径.R去倒推
存在或为+∞的前提下,不能由收敛半径.R去倒推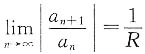 (或为0,或为+∞).
(或为0,或为+∞). ,则μ=______.
,则μ=______.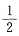 =P(△<0)=P(42-4X<0)=P(X>4)
=P(△<0)=P(42-4X<0)=P(X>4)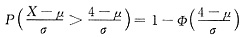
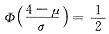 ,故可得
,故可得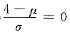 ,∴μ=4.
,∴μ=4. ,则P(Y≥1)=______.
,则P(Y≥1)=______.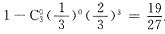 .
.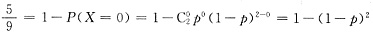 ,解得
,解得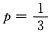 ,故P(Y≥1)=1-P(Y)=0)=
,故P(Y≥1)=1-P(Y)=0)=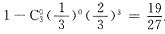 .
.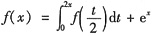 ,则f(x)=______.
,则f(x)=______.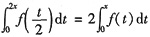 ,则
,则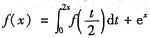 可化为f(x)=
可化为f(x)=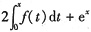 ,两边求导数得f'(x)-2f(x)=ex,解此一阶微分方程得
,两边求导数得f'(x)-2f(x)=ex,解此一阶微分方程得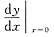 =______.
=______.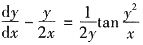 满足初始条件
满足初始条件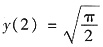 的特解是______.
的特解是______.
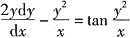 . 令y2=z,化为
. 令y2=z,化为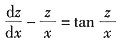 ①
①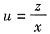 ,即z=xu,
,即z=xu,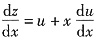 ,代入式①,得
,代入式①,得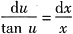 ,即
,即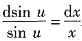 .
.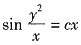 ,代入初始条件
,代入初始条件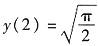 ,得
,得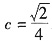 ,即有
,即有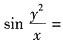
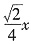 ,或
,或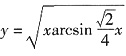 (由
(由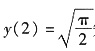 知y取算术根).
知y取算术根).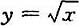 上任一点M(x,y)(x≥1)处的曲率半径,s=s(x)是该抛物线上介于点A(1,1)与M之间的弧长,求
上任一点M(x,y)(x≥1)处的曲率半径,s=s(x)是该抛物线上介于点A(1,1)与M之间的弧长,求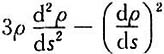 的值.
的值.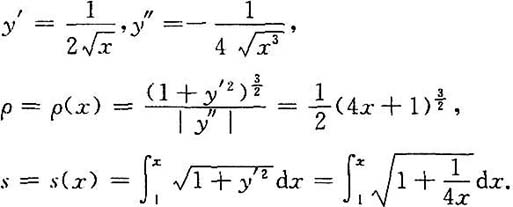
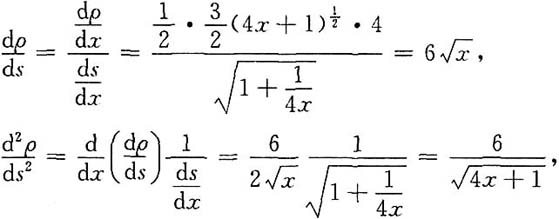
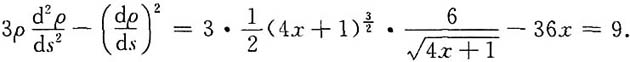
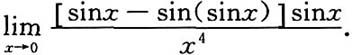
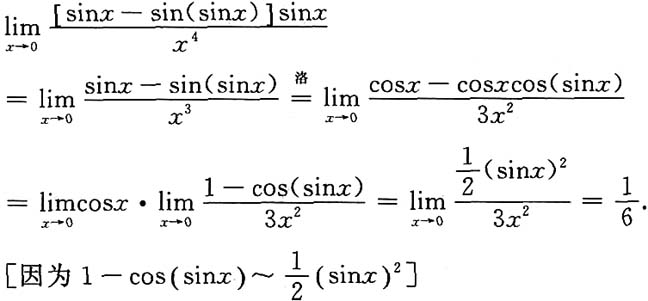
 求r(A)
求r(A)
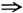 R(A)=n
R(A)=n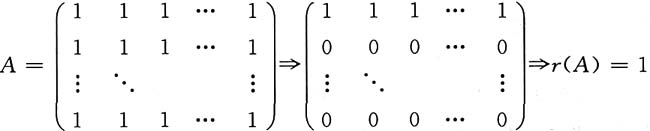

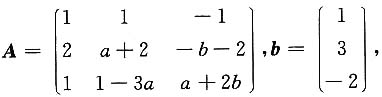 讨论当a,b取何值时,方程组AX=b无解、有唯一解、有无数个解,有无数个解时求通解.
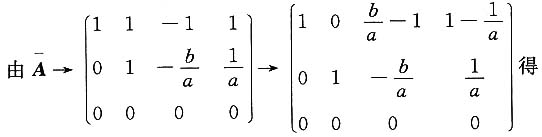
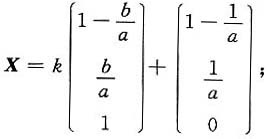
讨论当a,b取何值时,方程组AX=b无解、有唯一解、有无数个解,有无数个解时求通解.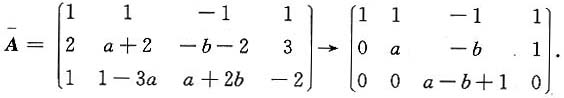
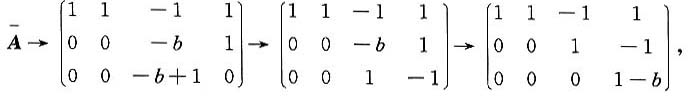
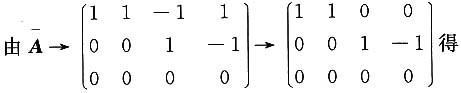
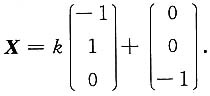
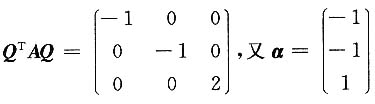 且A*α=α.
且A*α=α.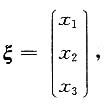 因为实对称矩阵不同特征值对应的特征向量正交,所以-x1-x2+x3=0,则A的属于特征值λ1=λ2=-1的线性无关的特征向量为
因为实对称矩阵不同特征值对应的特征向量正交,所以-x1-x2+x3=0,则A的属于特征值λ1=λ2=-1的线性无关的特征向量为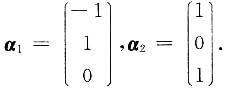
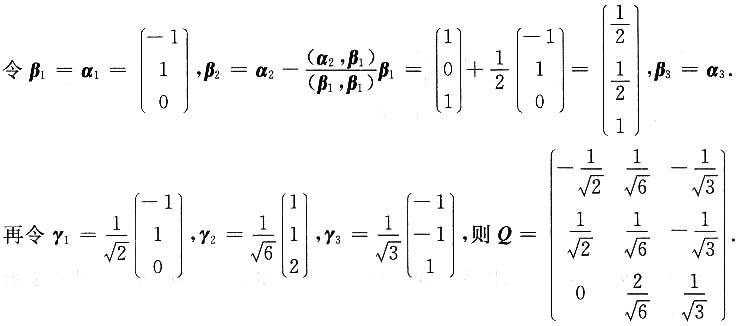
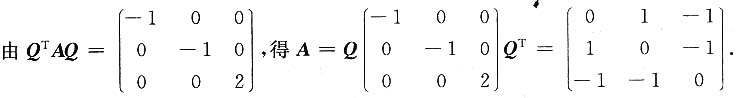
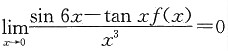 ,求
,求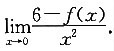
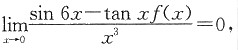
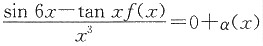 ,其中α(x)满足:
,其中α(x)满足: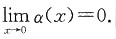
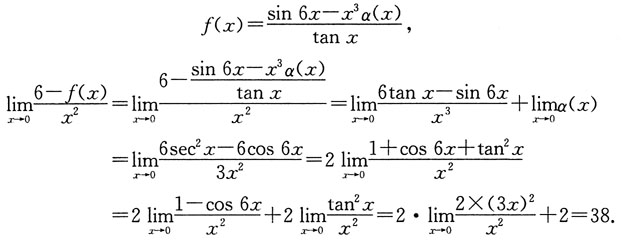
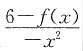 ,再取极限即可.
,再取极限即可.