银符考试题库B12
现在是：
试卷总分：150.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
专升本高等数学(一)模拟185
第Ⅰ卷(选择题)
一、选择题
(在每小题给出的四个选项中，只有一项是符合题目要求的)
1. 设
，则
等于______
A．
B．
C．
D．
A
B
C
D
A
2. 设f(x)在点x
0
处取得极值，则______
A.f'(x
0
)不存在或f'(x
0
)=0
B.f'(x
0
)必定不存在
C.f'(x
0
)必定存在且f'(x
0
)=0
D.f'(x
0
)必定存在，不一定为零
A
B
C
D
A
[解析] 若点x
0
为f(x)的极值点，可能为两种情形之一：
(1)若f(x)在点x
0
处可导，由极值的必要条件可知f'(x
0
)=0；
(2)如f(x)=|x|在点x=0处取得极小值，但f(x)=|x|在点x=0处不可导．这表明在极值点处，函数可能不可导．故选A．
3. 设
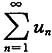
与
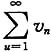
都是正项级数，且u
n
≤v
n
(n=1，2，…)，则下列命题正确的是______
A．若
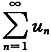
收敛，则
收敛
B．
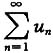
发散，则
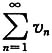
收敛
C．若
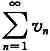
发散，则
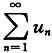
发散
D．
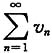
收敛，则
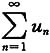
收敛
A
B
C
D
D
4. 设函数f(x)=sinx，则不定积分∫f'(x)dx=______．
A.sinx+C
B.cosx+C
C.-sinx+C
D.-cosx+C
A
B
C
D
A
[考点] 本题考查不定积分的性质．
[解析] 由∫f'(x)dx=f(x)+C，可知A选项正确．
提示 在不定积分的求解中，常数C不能省略．
5. 函数f(x)在区间[a，b]上连续是f(x)在[a，b]上可积的______
A.充分条件
B.必要条件
C.充分必要条件
D.既非充分又非必要条件
A
B
C
D
A
6. 曲线y=xe
-x
的拐点是______．
A.(1，e
-1
)
B.(2，e
-1
)
C.(0，0)
D.(2，2e
-2
)
A
B
C
D
D
[解析] y'=(1-x)e
-x
，y"=(x-2)e
-x
．令y"=0，解得x=2．
因为当x＜2时，y"＜0；当x＞2时，y"＞0．因此(2，2e
-2
)为曲线的拐点．
7. 幂级数
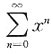
的收敛半径为______
A.1
B.2
C.3
D.4
A
B
C
D
A
[解析] 由于
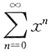
中a
n
=1，因此a
n+1
=1，
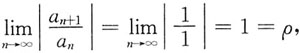
可知收敛半径
故选A．
8. 设幂级数
在x=3处收敛，则该级数在x=-2处______
A.发散
B.条件收敛
C.绝对收敛
D.收敛性不能确定
A
B
C
D
C
[考点] 无穷级数在一点处的敛散性．
[解析] 由题意可知，幂级数
的收敛半径最小值等于3，所以该级数在x=-2处绝对收敛．
9. 函数
在点x=0处______
A.不连续
B.可导
C.连续但不可导
D.以上都不对
A
B
C
D
C
10. 设F(x，y)=xy+2lnx+3lny-1≡0，则y'等于______
A．
B．
C．
D．
A
B
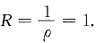
C
D
A
第Ⅱ卷(非选择题)
二、填空题
1. 设区域D由曲线y=x
2
，y=1围成，则
=______．
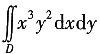
0
[解析] 由区域D的图形特征可知，该区域关于y轴对称，且被积函数x
3
y
2
是关于x的奇函数，所以
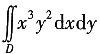
=0．
2. 估计积分的值______＜
＜______．
1，e
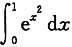
3. 求
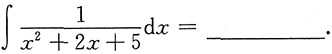
[考点] 不定积分的计算．
[解析]
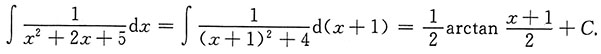
4. 若
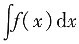
=x
2
+C，则
=______．
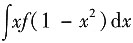
x
2
-
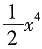
+C
[解析] 由
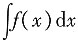
=x
2
+C，可得f(x)=(x
2
)'=2x．因此
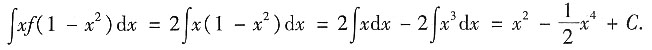
5. 设a＜x＜b时，f'(x)=g'(x)，则f(x)与g(x)的关系为f(x)=______．
g(x)+c(c是常数)
6.
=______．
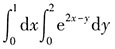
[解析]
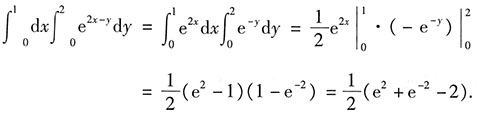
7.
=______．
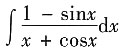
ln|x+cosx|+C
[解析] 利用凑微分法求解该不定积分，则有
=ln|x+cosx|+C．
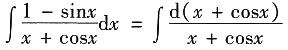
8. ∫xdf'(x)=______．
xf'(x)-f(x)+c
9. 若
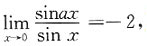
则a=______．
-2
[解析] 因为
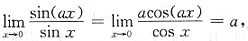
所以a=-2．
10. 设
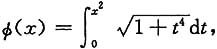
则
=______．
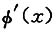
三、解答题
(共70分．解答应写出推理、演算步骤)
求下列函数的微分：
1. y=xlnx+sin(x
2
)；
解：求微分有两种方法：运用微分定义dy=f'(x)dx，求出f'(x)后代入即得；或利用一阶微分形式不变性和微分运算法则求微分．
因为y'=lnx+1+2xcosx
2
，故dy=(1+lnx+2xcosx
2
)dx．
或dy=d(xlnx+sinx
2
)=d(xlnx)+d(sinx
2
)
=lnxdx+xd(lnx)+cosx
2
d(x
2
)
=lnxdx+dx+2xcosx
2
dx
=(1+lnx+2xcosx
2
)dx．
2. y=x
cosx
．
解：
3. 判断级数
的敛散性．
解：
由此得到，
4. 求极限
，其中m，n是常数．
解：e
mn
5. 把f(x)=cos
2
x展开为x的幂级数．
解：因
故
6. 判定级数
的收敛性．若收敛，是绝对收敛，还是条件收敛?
解：所给级数是任意项级数，不是交错级数．由于
又由于
的p级数，因而收敛．由正项级数的比较判别法可知
收敛，从而
绝对收敛．
[解析] 这是一道任意项级数判断敛散性的题，首先清楚如果给了一个任意项级数
那么先看看
是否收敛．如收敛，则原级数
绝对收敛．如
发散，但原级数
收敛，则称
条件收敛．
7. 计算
解：令
，x=t
2
，dx=2tdt．
当x=4时，t=2；当x=9时，t=3．
则有
[解析] 本题采用凑微分法．即
，也可采用上面的方法来解．
8. 求
在x=1处的导数．
解：
故
9. 按定义求
在点x=1和X处的导数．
解：
根据导数定义求函数的导数，如果是求在一点处的导数，用
求较方便；如果是求在任意一点处的导数，用
较方便．
第Ⅰ卷(选择题)一、选择题
1
2
3
4
5
6
7
8
9
10
第Ⅱ卷(非选择题)二、填空题
1
2
3
4
5
6
7
8
9
10
三、解答题
1
2
3
4
5
6
7
8
9
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
，则
等于______
与
都是正项级数，且un≤vn(n=1，2，…)，则下列命题正确的是______
收敛，则
收敛
发散，则
收敛
发散，则
发散
收敛，则
收敛
的收敛半径为______
中an=1，因此an+1=1，
故选A．
在x=3处收敛，则该级数在x=-2处______
的收敛半径最小值等于3，所以该级数在x=-2处绝对收敛．
在点x=0处______
=______．
＜______．
=x2+C，则
=______．
+C
=x2+C，可得f(x)=(x2)'=2x．因此
=______．
=______．
=ln|x+cosx|+C．
则a=______．
所以a=-2．
则
=______．
的敛散性．
，其中m，n是常数．
的收敛性．若收敛，是绝对收敛，还是条件收敛?
的p级数，因而收敛．由正项级数的比较判别法可知
绝对收敛．
那么先看看
是否收敛．如收敛，则原级数
绝对收敛．如
发散，但原级数
收敛，则称
条件收敛．
，x=t2，dx=2tdt．
，也可采用上面的方法来解．
在x=1处的导数．
在点x=1和X处的导数．
求较方便；如果是求在任意一点处的导数，用
较方便．
深色：已答题 浅色：未答题