第Ⅰ卷(选择题)
一、选择题(在每小题给出的四个选项中，只有一项是符合题目要求的)5. 设函数y=f(x)在点x
0处可导，且下式各极限都存在，其中一定成立的是______
A．
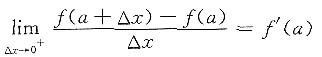
B．
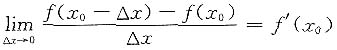
C．
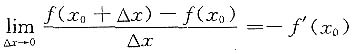
D．
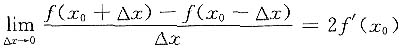
A B C D
D
[解析] 因为
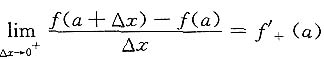
，不一定等于f'(a)，或f'(a)不存在，故A不成立．
对B，
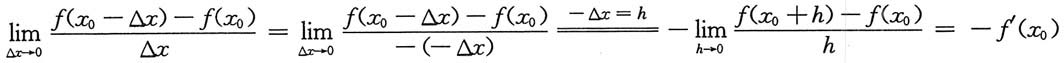
故B不正确．
由定义，知C不成立，故应选D．事实上
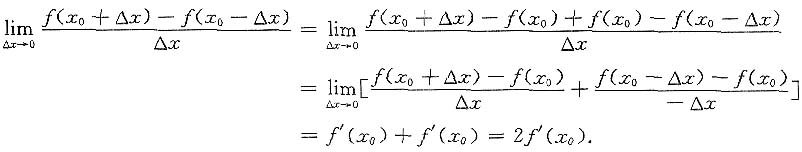
6. 幂级数
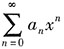
在点x=3处收敛，则级数
______
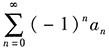
- A.绝对收敛
- B.条件收敛
- C.发散
- D.收敛性与an有关
A B C D
A
[解析] 由于幂级数
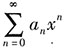
在点x=3处收敛，可知该幂级数的收敛半径
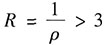
，其中
，从而可得
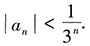
由几何级数
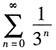
收敛，知
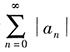
收敛．因此
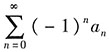
绝对收敛．
第Ⅱ卷(非选择题)
二、填空题1. 曲线y=x
3-6x的拐点坐标为______．
(0，0)
[解析] 由y=x3-6x，得y'=3x2-6，y"=6x．令y"=0，得到x=0．
当x=0时，y=0．当x＜0时，y"＜0；当x＞0时，y"＞0．
因此点(0，0)是曲线y=x3-6x的拐点．
2. 函数
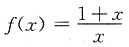
在[1，2]上符合拉格朗日中值定理的ξ=______．
[解析] 由拉格朗日中值定理有
解得ξ
2=2．
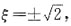
其中
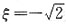
(舍)，得
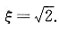
3. 设f(x)的二阶导数存在，y=ln[f(x)]，则y"=______．
4. 微分方程
满足初始条件y|
x=1=0的特解为______．
[解析] 由一阶线性微分方程的通解公式有
由初始条件y|
x=1=0，得C=0，故所求特解为
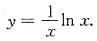
5. f(x)在x
0处连续的______是
．
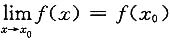
6. 设函数
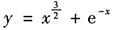
，则y"=______．
[解析]
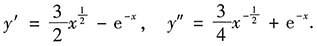
7. 设
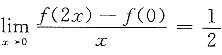
，则f'(0)=______．
8. 设
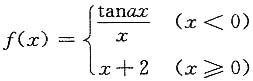
在点x=0处连续，则a=______．
9. 设z=u
2·lnv，u=
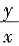
，v=
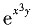
，则dz=______．
y3dx+3xy2dy
[解析] 将u=
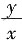
，v=
代入z=u
2·lnv，可得z=xy
3．因此
dz=d(xy
3)=y
3dx+3xy
2dy．
10. 过点(1，-1，0)与直线
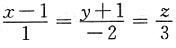
垂直的平面方程为______．
x-2y+3z-3=0或(x-1)-2(y+1)+3z=0
[解析] ∵直线垂直于平面π，∴π的法向量即为直线的方向向量，即n=s={1，-2，3}，且点(1，-1，0)在平面π上∴(x-1)-2(y+1)+3z=0．
三、解答题(共70分．解答应写出推理、演算步骤)1. 计算
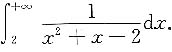
解：
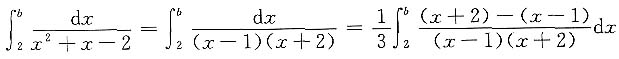
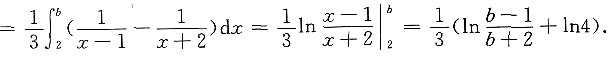
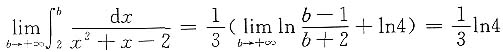
，故
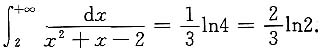
注意 在题中涉及lnx的结果，由于x的积分区间均大于零，我们均去掉了绝对值符号．
2.
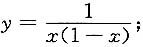
解：
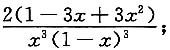
3. y=xlnx；
解：
4.
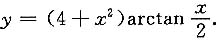
解：
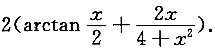
5. 当x＞1时，
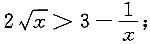
证：设
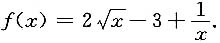
6. 当x≥0时，2xarctanx≥ln(1+x
2)．
解：设f(x)=2xarctanx-ln(1+x2)．
7. 设函数y=y(x)由方程cos(x+y)+y=1确定，求
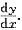
解：
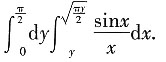
8. 交换积分次序；
解：二次枳分的积分区域D可表示为
y≤x≤
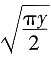
，0≤y≤
，
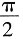
根据积分区域的图形特征可知，交换积分次序后，区域D又可表示为
0≤x≤
，
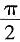
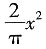
≤y≤x．
因此
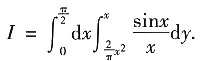
9. 求Ⅰ的值．
解：由被积函数的特征可知，应选择先对y积分，再对x积分．
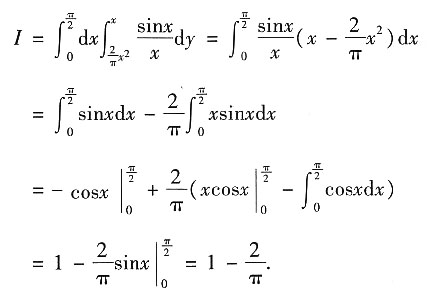
10. 求
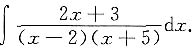
解：原式
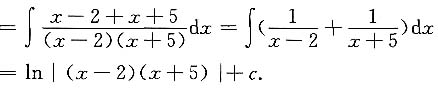
对被积函数进行分解，可采用如下方法：
设
比较两端等式得
2x+3=A(x+5)+B(x-2)，
令x=-5，得B=1；令x=2，得A=1．
也可以比较等式两端的系数2x+3=(A+B)x+5A-2B，得
x的系数：2=A+B
x'的系数：3=5A-2B
解得
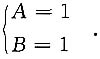
11. 计算
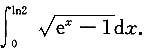
解：设
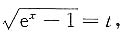
则
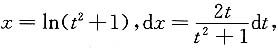
当x=0时，t=0；x=ln2时，t=1．
原式
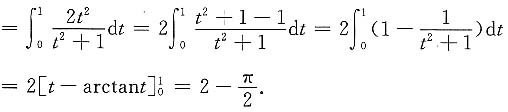
12. 设z=z(x，y)由方程e
z-xy+y+z=0确定，求dz．
解：解法一 令F(x，y，z)=e
z-xy+y+z，则
f'
x=-y，f'
y=-x+1，f'
z=e
z+1．
因此
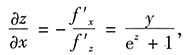
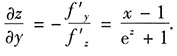
从而可得
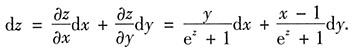
解法二 对方程e
z-xy+y+z=0两端直接取微分，则有
d(e
z-xy+y+z)=de
z-d(xy)+dy+dz=0，
即e
zdz-ydx-xdy+dy+dz=0．
整理可得
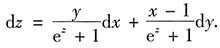
[考点] 本题考查求二元隐函数的偏导数与全微分．
，则
=______．
是______
在点x=0连续，则k等于______
深色：已答题 浅色：未答题