一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 已知α,β,γ
1,γ
2,γ
3均为4维列向量,若|A|=|α,γ
1,γ
2,γ
3|=3,|B|=|β,γ
1,γ
2,γ
3|=1,则|A+2B|=______
A B C D
A
[解析] 由A+2B=(α+2β,3γ1,3γ2,3γ3)
知|A+2B|=27|α+2β,γ1,γ2,γ3|
=27(|A|+2|B|)=135.
2. 设

,记
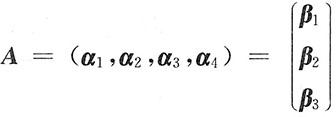
,且
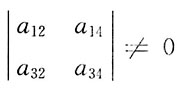
,

,下列结论:①r(A)=2;②α
2,α
4线性无关;③β
1,β
2,β
3线性相关;④α
1,α
2,α
3线性相关.正确的是______
A B C D
D
[解析] 对于①,由
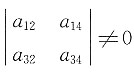
知,r(A)≥2,但

,不能得到r(A)<3(所有3阶子式全为0才可以得到r(A)<3),所以①错误.
对于②,由
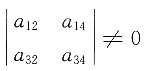
知,
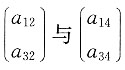
线性无关,于是增加分量得
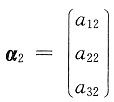
与
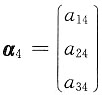
仍线性无关,所以②正确.
对于③,由

知,(a
11,a
12,a
13),(a
21,a
22,a
23),(a
31,a
32,a
33)线性相关,但增加分量后得到的β
1,β
2,β
3不一定线性相关,故③不正确.
对于④,由

知,α
1,α
2,α
3线性相关,故④正确.
选D.
6. 设D={(x,y)|0≤x≤π,0≤y≤π},则
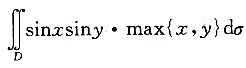
等于______
A.π
B.
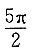
C.
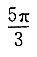
D.
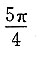
A B C D
B
[解析] 根据对称性,令D
1={(x,y)|0≤x≤π,0≤y≤x},
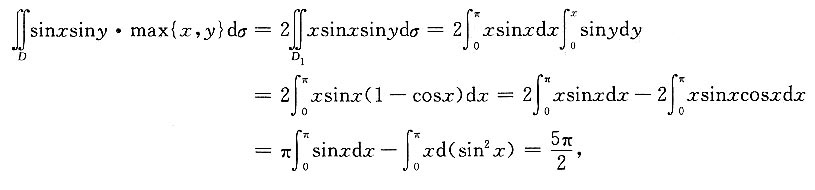
选B.
二、填空题1. 设A是n阶方阵,A
*为A的伴随矩阵,|A|=5,则方阵B=AA
*的特征值是______,特征向量是______.
2. 曲线L的极坐标方程是r=θ,则L在点
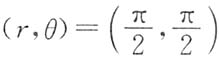
处的切线的直角坐标方程是______.
[解析] 先把曲线方程化为参数方程
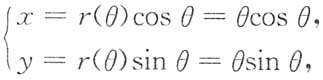
于是在
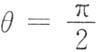
处,x=0,
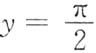
,

,则L在点

处的切线方程为
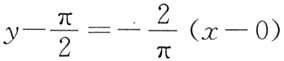
,即
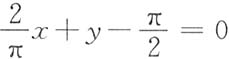
.
3. 微分方程xy'+x
2y"=y
'2满足初始条件y|
x=0=2,y'|
x=1=1的特解是______.
y=ln(1+x2)+2
[解析] 令y'=p(x),则
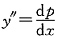
,于是
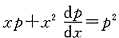
,即

令

,则p=ux,
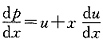
,于是
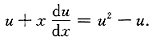
分离变量得
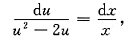
两端积分
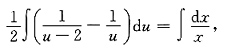
得
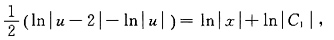
从而
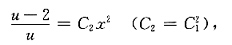
即
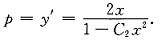
由y'|
x=1-1得C
2=-1,故
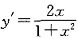
.于是
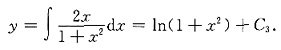
又由y|
x=0=2得C
3=2,故所求特解为y=ln(1+x
2)+2.
4. 设a为常数,[x]表示不超过x的最大整数,又设
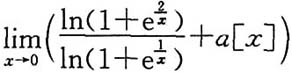
存在,则a=______,上述极限值=______.
-2;2
[解析] [x]表示不超过x的最大整数,例如[π]=3,[-π]=-4.所以
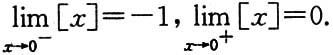
因此对于所讨论的极限应分x→0
-与x→0
+讨论.
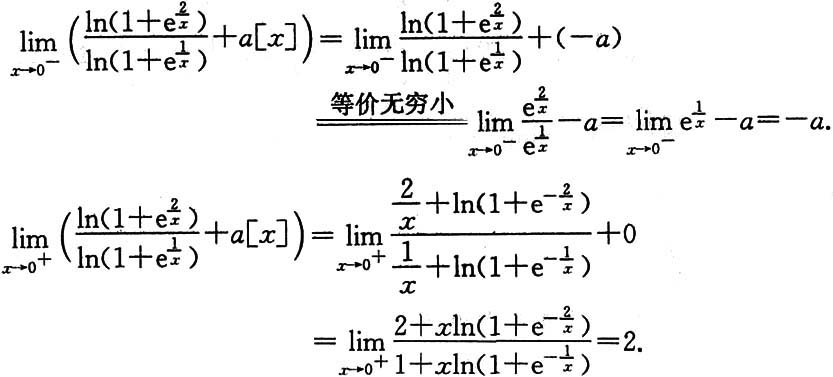
所以当且仅当a=-2时上述极限存在,该极限值为2.
5. 已知4阶矩阵A相似于B,A的特征值为2,3,4,5,E为4阶单位矩阵,则|B-E|=______.
6. 设

则f'(x)=______.
三、解答题(本大题共70分.解答应写出文字说明、证明过程或演算步骤.)1. 设函数f(x)连续,证明
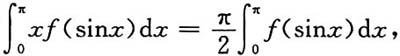
并计算积分
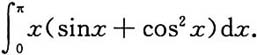
2. 设

.求
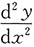
.
3. 求二重积分
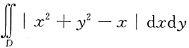
,其中D={(x,y)|0≤y≤1-x,0≤x≤1}.
解:方法一:
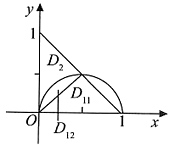
在区域D内作圆x
2+y
2=x,将区域D分为D
1,D
2,则
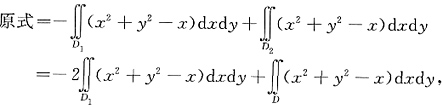
第一卦限的角平分线将D
1分为D
11及D
12,
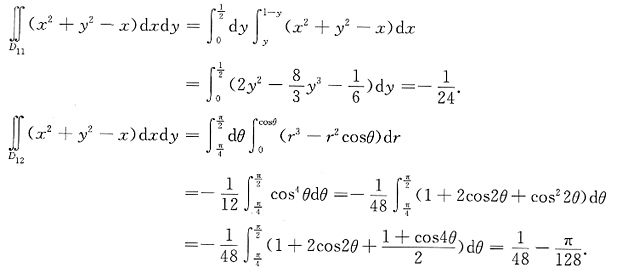
而
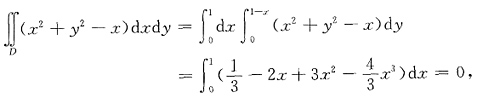

方法二:
在区域D内作圆x
2+y
2=x,将区域D分为D
1,D
2,则
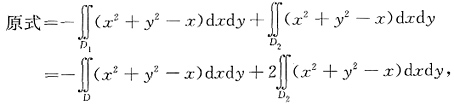
而
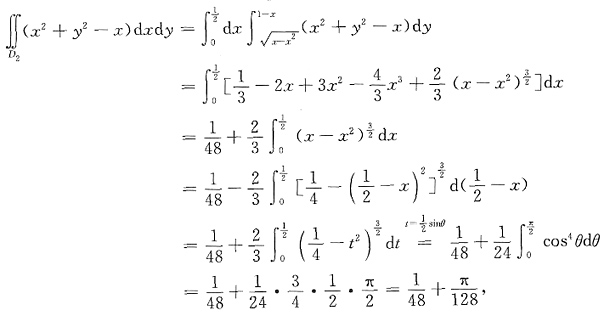
又
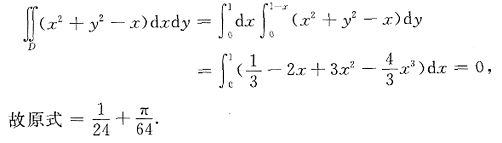
4. 已知函数y=y(x)(0≤x≤1)满足微分方程yy"=(y')
2,且y(0)=1.已知曲线y=y(x)与直线x=0,x=1,y=0所围成的平面区域D的面积为e-1.求D绕y轴旋转所得的旋转体体积.
解:令y'=p(y),则

,于是

分离变量得

两端积分得ln|p|=ln|y|+ln|C
1|,
从而p=y'=C
1y,
即
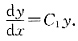
分离变量得
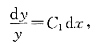
两端积分得ln|y|=C
1x+ln|C
2|,
即y=C
2e
c1x 由y(0)=1得C
2=1,故y=e
C1x.
由题意,
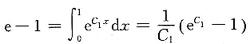
,解得C
1=1,因此
y=e
x.
故所求体积为
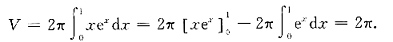
所求体积的解法是基于下面的命题:平面图形0≤a≤x≤b,0≤y≤f(x)绕y轴旋转所得旋转体的体积为
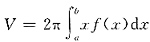
.该体积也可用如下方法求:
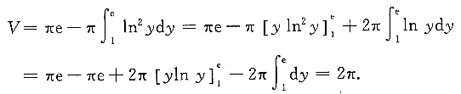
5. 已知f(x)在[0,1]上连续,对任意x,y都有|f(x)-f(y)|<M|x-y|,证明:
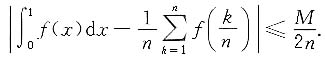
证:因为
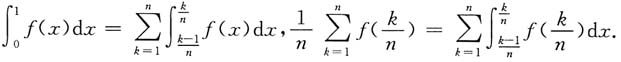
所以
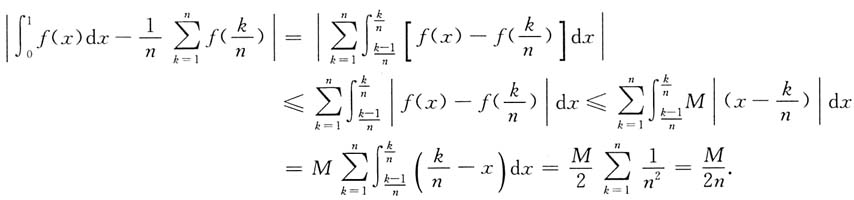
6. 设f"(u)存在,y=f(x+y),求
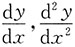
.
解:令u=x+y,对y=f(u)两边关于x求导,得

即

对式①两边关于x求导,有
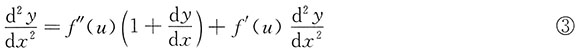
再将式②代入式③,整理可得
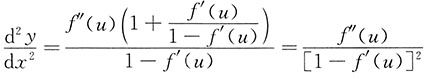
[考点] 连续、导数、微分(Ⅰ)