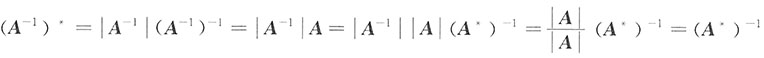一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 曲线
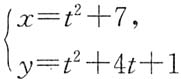
上对应于t=1的点处的曲率半径是______
A.
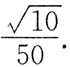
B.
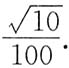
C.
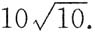
D.
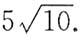
A B C D
C
[解析] 曲线在点(x,f(x))处的曲率公式
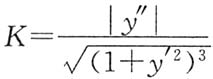
,曲率半径
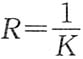
.
本题中
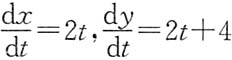
,所以
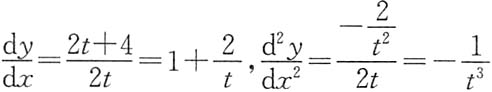
,对应于t=1的点处有y'=3,y"=-1,所以
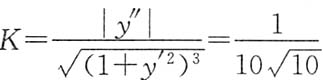
,曲率半径
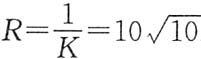
.应选C.
2. 设常数0<a<1,区域D由x轴,y轴,直线x+y=a以及x+y=1围成.
记
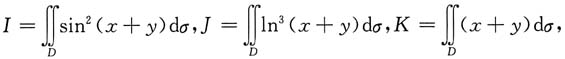
则I,J,K的大小关系是______
- A.J<K<I.
- B.J<I<K.
- C.I<J<K.
- D.I<K<J.
A B C D
B
[解析] 在区域D上有0<x+y≤1,于是
ln
3(x+y)≤0≤sin
2(x+y)≤(x+y)
2≤(x+y),且它们互不恒等,连续,因此,它们在D上的积分值满足

应选B.
4. 设cosx-1=xsinα(x),其中
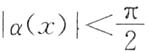
,则当x→0时,α(x)是______
- A.比x高阶的无穷小量.
- B.比x低阶的无穷小量.
- C.与x同阶但不等价的无穷小量.
- D.与x等价的无穷小量.
A B C D
C
[解析] 因为cosx-1=xsinα(x),所以
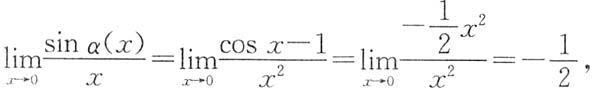
即有
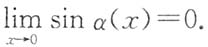
注意到
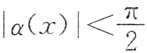
,可知
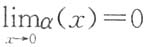
,即α(x)是x→0时的无穷小量,且
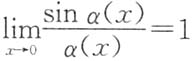
,故
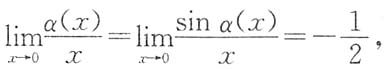
即α(x)是与x同阶但不等价的无穷小量,选项C正确.
5. 矩形闸门宽a米,高度h米,垂直放在水中,上边与水面相齐,闸门压力为______.
A.
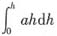
B.
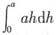
C.
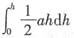
D.
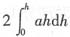
A B C D
A
[考点] 定积分在物理中的应用
[解析] 取[x,x+dx]

[0,h],dF=1·x·a·dx=axdx,
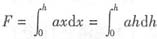
,选(A).
6. 下列各选项正确的是______
A.若
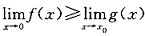
,则存在a>0,使得当0<|x-x
0|<δ时,有f(x)≥g(x).
B.若存在δ>0,使得当0<|x-x
0|<δ时,有f(x)>g(x),且
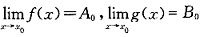
,则A
0>B
0.
C.若存在δ>0,使得当0<|x-x
0|<δ时,有f(x)>g(x),则

.
D.若
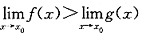
,则存在δ>0,使得当0<|x-x
0|<δ时,有f(x)>g(x).
A B C D
D
[解析] A考查保号性(极限值的大小推函数值的大小),错在“条件和结论中的≥都应改为>”;B考查保号性的推论(函数值的大小推极限值的大小),错在“结论中的>应改为≥”;C考查保号性的推论(函数值的大小推极限值的大小),错在“没说极限存在”;D正确.
7. 由下列四个条件
①f(x)=(x-a)φ(x),其中φ(x)在x=a连续.
②f(x)=|x-a|φ(x),其中φ(x)在x=a连续且φ(a)≠0.
③存在δ>0,使对任意x∈(a-δ,a+δ),有|f(x)|≤L|x-a|
λ,其中λ>1为常数.
④
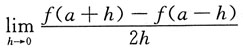
存在.
能分别推出f'(a)存在的条件是______
- A.①,④.
- B.①,③.
- C.①,③,④.
- D.①,②,③,④.
A B C D
B
[解析] 由①可推出f'(a)存在,因为由①有:
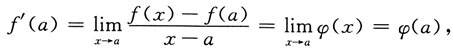
故f'(a)=φ(a).
由②不能推出f'(a)存在,由导数定义可得:
f'
+(a)=φ(a),f'
-(a)=-φ(a).
因为φ(a)≠0,所以有f'
+(a)≠f'
-(a),故f'(a)不存在.
由③可推出f'(a)存在,因为在不等式中取x=a,知f(a)=0,故当λ>1时,有
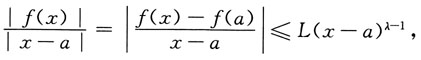
于是
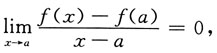
即f'(a)=0.
由④不能推出f'(a)存在,例如:
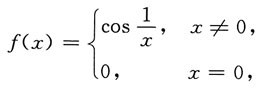
则f(x)在x=0处不连续,因此f(x)在x=0不可导,
但是
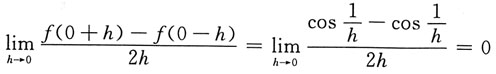
存在.故应选B.
9. 微分方程y"-4y'+8y=e
2x(1+cos2x)的特解可设为y
k=______
- A.Ae2x+e2x(Bcos2x+Csin2x)
- B.Axe2x+e2x(Bcos2x+Csin2x)
- C.Ae2x+xe2x(Bcos2x+Csin2x)
- D.Axe2x+xe2x(Bcos2x+Csin2x)
A B C D
C
[解析] 特征方程为:
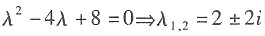
∵f(x)=e
2x(1+cos2x)=e
2x+e
2xcos2x,∴
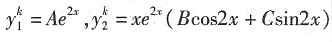
故特解为:
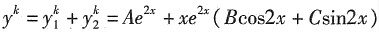
,选C.
10. 设函数f(x)在连续,其一阶导函数除x=a外都存在,并且其一阶导函数的图形如下图所示,则f(x)______
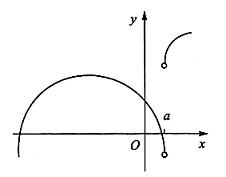
- A.有两个极大值点,一个极小值点,一个拐点.
- B.有一个极大值点,一个极小值点,两个拐点.
- C.有一个极大值点,一个极小值点,一个拐点.
- D.有一个极大值点,两个极小值点,两个拐点.
A B C D
D
[解析] 为方便表示,故在图中加上字母,如下图所示,一共加了两个字母,分别是x
1,x
2.
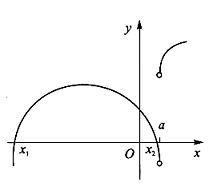
关注极值点.
极值点肯定来自于一阶导数为0的点或者一阶导数没有定义的点,从图中可以非常直观地看出,一阶导数为0的点是x=x
1和x=x
2,一阶导数没有定义的点是x=a.
下面来验证这三个点,
首先,看点x=x
1,由于在点x=x
1,的左去心邻域内f'(x)<0,点x=x
1的右去心邻域内f'(x)>0,故x=x
1是函数f(x)的一个极小值点.
接着,看点x=x
2.由于在点x=x
2的左去心邻域内f'(x)>0,点x=x
2的右去心邻域内f'(x)<0,故x=x
2是函数f(x)的一个极大值点.
最后,看点x=a,由于在点x=a的左去心邻域内f'(x)<0,点x=a的右去心邻域内f'(x)>0,故x=a是函数f(x)的一个极小值点,
综上所述,函数y=f(x)有一个极大值点,有两个极小值点.
二、填空题1. 若二阶常系数线性齐次微分方程2y"+ay'=0和y"-by=0有同一解y=e
2x,则非齐次方程y"+ay'+by=e
2x的通解为y=______.
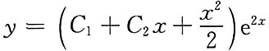
(C
1,C
2为任意常数)
[解析] 由题设条件可知二次方程2λ
2+aλ=0与λ
2-b=0有共同的一个解λ=2,所以b=4,a=-4.齐次微分方程为y"-4y'+4y=0,其通解是y=(C
1+C
2x)e
2x(C
1,C
2为任意常数).
求非齐次微分方程y"-4y'+4y=e
2x的一个特解:
设特解Y=Ax
2e
2x,代入微分方程y"-4y'+4y=e
2x,得
A(2e
2x+8xe
2x+4x
2e
2x)-4A(2xe
2x+2x
2e
2x)+4Ax
2e
2x=e
2x.
比较系数,得
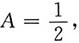
故其特解为
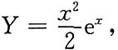
通解为
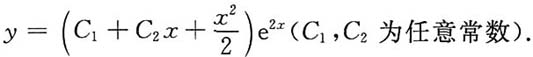
2. 抛物线
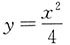
与过点A(2,1)处法线所围成的图形的面积为______.
3.
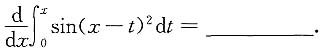
4. 设
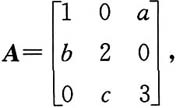
其中abc=-6,A
*是A的伴随矩阵,则A
*有非零特征值______.
11
[解析] 因abc=-6,故
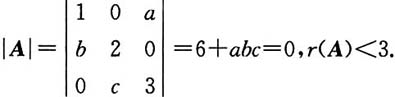
又
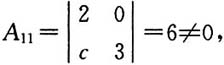
故r(A)=2,r(A
*)=1.
故A
*有特征值
λ
1=λ
2=0,
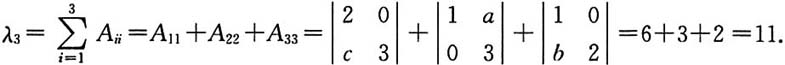
5. 若对任意的n×1矩阵X,均有AX=O,则A=______.
6. 函数y=x+2cosx在
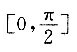
上的最大值为______.
[解析] 令y'=1-2sinx=0得

y"=-2cosx,因为
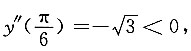
所以
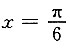
为y=x+2cosx的极大值点,也是最大值点,故最大值为
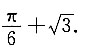
三、解答题(本大题共70分.解答应写出文字说明、证明过程或演算步骤.)1. 设
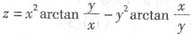
,求
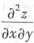
.
解:按照复合函数偏导的方法,得
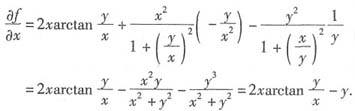
再对y求偏导数,有
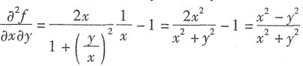
.
[考点] 复合函数求偏导数
2. 计算
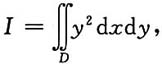
其中D是由直线x=-2,y=2,x轴及曲线
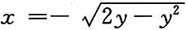
所围成.
解:积分区域如图所示.
选择先x后y的积分次序,得
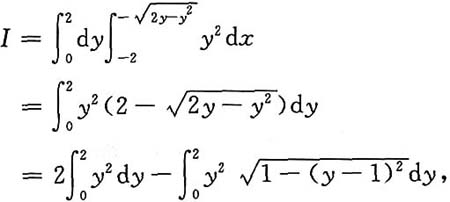
令t=y-1,得
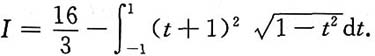
利用对称区间上奇偶函数积分性质及定积分几何意义可得
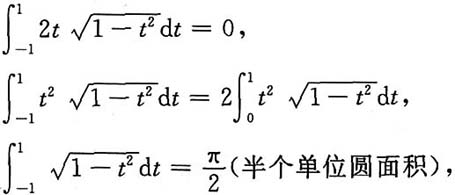
所以
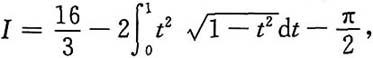
令t=sinθ,得
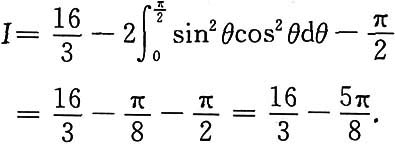
3. 求
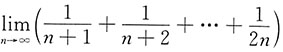
.
解:
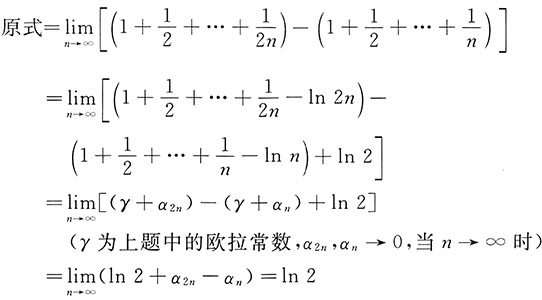
注 本题也可以利用定积分的定义计算.
[考点] 函数、极限
4. 求f(x)=|x
2-3x+2|在闭区间[-10,10]上的最值.
解:令x
2-3x+2=0得x=1,2.由于f(x)≥0,故在[-10,10]上,即当x=1,2时,函数取得最小值m=0.
f'(x)=(2x-3)sgn(x
2-2x+3)=(2x-3)sgn[(x-1)
2+2](x≠1,2).当
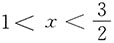
时,f'(x)>0;当
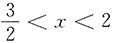
时,f'(x)<0.
所以,当

时有极大值
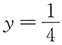
,于是最大值
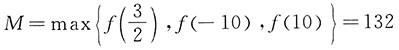
[考点] 连续、导数、微分(Ⅱ)
5. 设f(x)在[0,1]上可微,且当x∈(0,1)时,0<f'(x)<1,f(0)=0.试证

证1:问题等价于证明
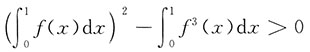
令
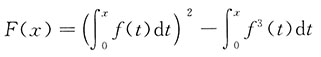
因F(0)=0,故只要证明在(0,1)内有F'(x)>0.事实上,有
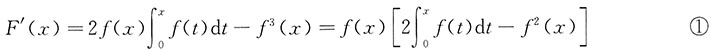
已知f(0)=0,0<f'(x)<1(当x∈(0,1)),故x∈(0,1)时f(x)>0(以下证式①中另一因子大于零).记
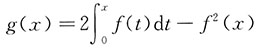
,则g(0)=0,且
g'(x)=2f(x)-2f(x)·f'(x)=2f(x)[1-f'(x)]>0
于是
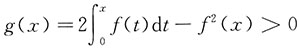
即F'(x)>0获证.从而命题得证.
证2:问题在于证明
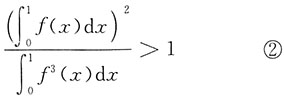
令

.对式②左边应用柯西中值定理,存在0<ξ<1,有
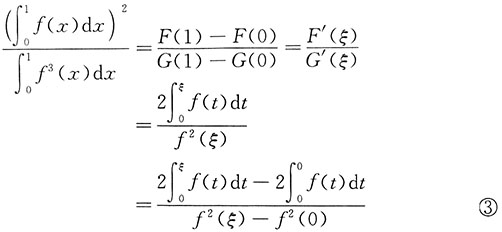
对于函数

,在[0,ξ]上再利用柯西中值定理,可得
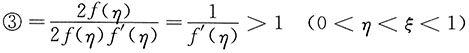
[考点] 一元函数微积分
6. (A
-1)
*=(A
*)
-1;
证:A可逆,
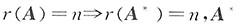
也可逆,且有
A
-1(A
-1)
*=|A
-1|E
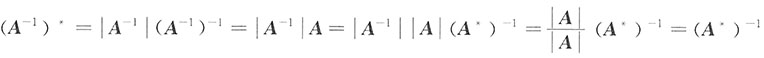
[考点] 矩阵
7. (AB)
*=B
*A
*.
证:B*A*=|B|B-1|A|A-1=|AB|(AB)-1=(AB)*.
[考点] 矩阵
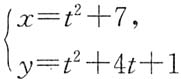 上对应于t=1的点处的曲率半径是______
上对应于t=1的点处的曲率半径是______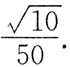
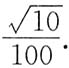
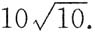
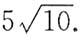
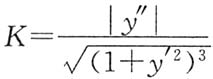 ,曲率半径
,曲率半径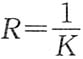 .
.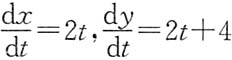 ,所以
,所以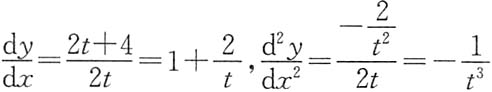 ,对应于t=1的点处有y'=3,y"=-1,所以
,对应于t=1的点处有y'=3,y"=-1,所以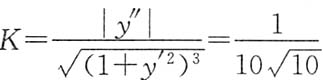 ,曲率半径
,曲率半径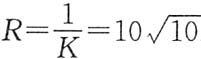 .应选C.
.应选C.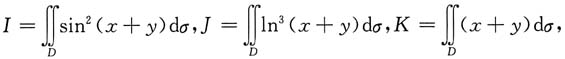 则I,J,K的大小关系是______
则I,J,K的大小关系是______
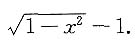
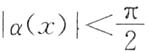 ,则当x→0时,α(x)是______
,则当x→0时,α(x)是______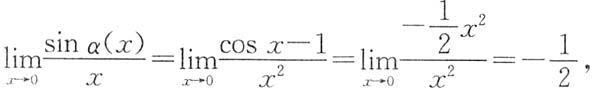
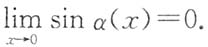
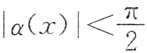 ,可知
,可知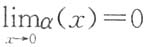 ,即α(x)是x→0时的无穷小量,且
,即α(x)是x→0时的无穷小量,且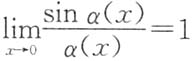 ,故
,故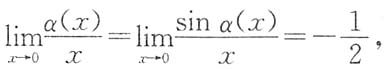
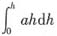
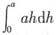
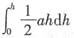
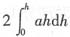
 [0,h],dF=1·x·a·dx=axdx,
[0,h],dF=1·x·a·dx=axdx,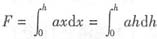 ,选(A).
,选(A).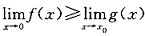 ,则存在a>0,使得当0<|x-x0|<δ时,有f(x)≥g(x).
,则存在a>0,使得当0<|x-x0|<δ时,有f(x)≥g(x).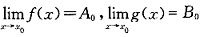 ,则A0>B0.
,则A0>B0. .
.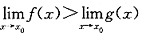 ,则存在δ>0,使得当0<|x-x0|<δ时,有f(x)>g(x).
,则存在δ>0,使得当0<|x-x0|<δ时,有f(x)>g(x).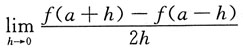 存在.
存在.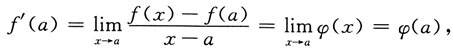 故f'(a)=φ(a).
故f'(a)=φ(a).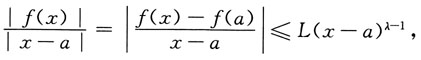
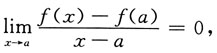 即f'(a)=0.
即f'(a)=0.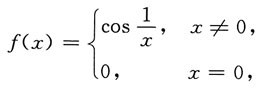 则f(x)在x=0处不连续,因此f(x)在x=0不可导,
则f(x)在x=0处不连续,因此f(x)在x=0不可导,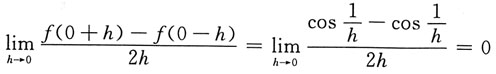 存在.故应选B.
存在.故应选B.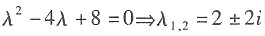
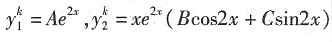
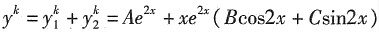 ,选C.
,选C.

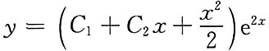 (C1,C2为任意常数)
(C1,C2为任意常数)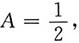 故其特解为
故其特解为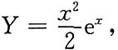 通解为
通解为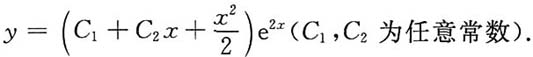
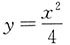 与过点A(2,1)处法线所围成的图形的面积为______.
与过点A(2,1)处法线所围成的图形的面积为______.
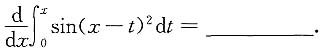
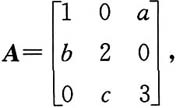 其中abc=-6,A*是A的伴随矩阵,则A*有非零特征值______.
其中abc=-6,A*是A的伴随矩阵,则A*有非零特征值______.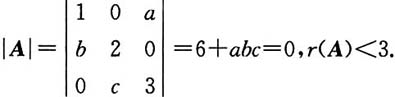
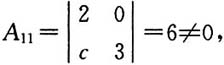 故r(A)=2,r(A*)=1.
故r(A)=2,r(A*)=1.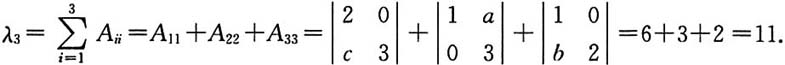
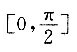 上的最大值为______.
上的最大值为______.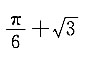

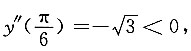 所以
所以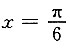 为y=x+2cosx的极大值点,也是最大值点,故最大值为
为y=x+2cosx的极大值点,也是最大值点,故最大值为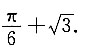
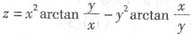 ,求
,求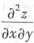 .
.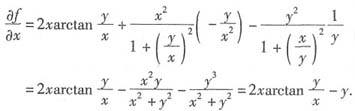
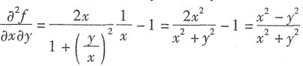 .
.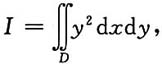 其中D是由直线x=-2,y=2,x轴及曲线
其中D是由直线x=-2,y=2,x轴及曲线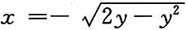 所围成.
所围成.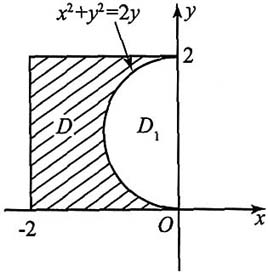
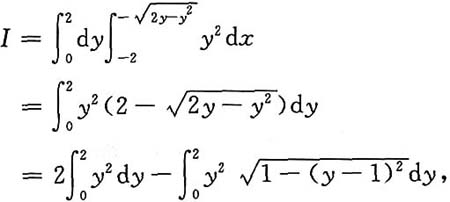
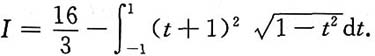
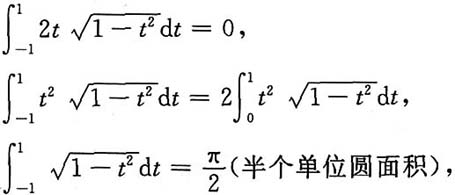
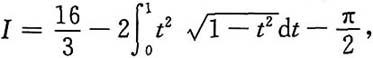
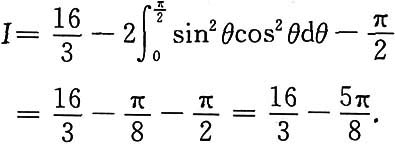
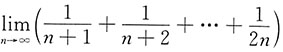 .
.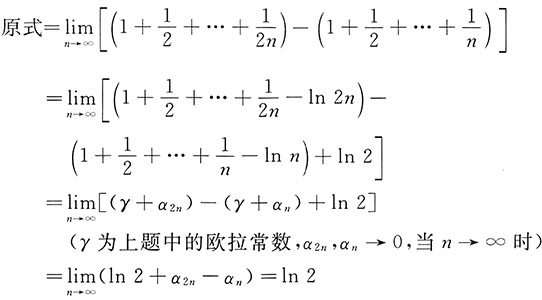
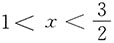 时,f'(x)>0;当
时,f'(x)>0;当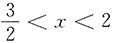 时,f'(x)<0.
时,f'(x)<0. 时有极大值
时有极大值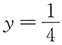 ,于是最大值
,于是最大值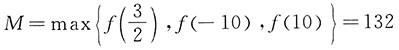

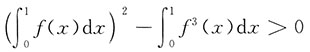
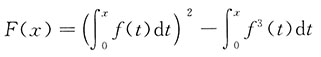
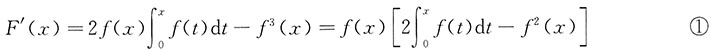
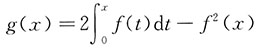 ,则g(0)=0,且
,则g(0)=0,且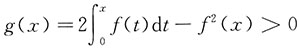
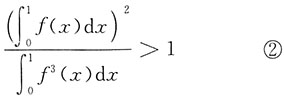
 .对式②左边应用柯西中值定理,存在0<ξ<1,有
.对式②左边应用柯西中值定理,存在0<ξ<1,有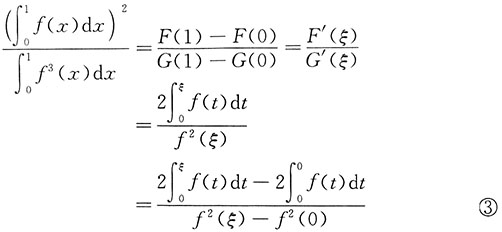
 ,在[0,ξ]上再利用柯西中值定理,可得
,在[0,ξ]上再利用柯西中值定理,可得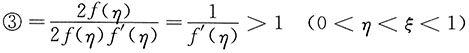
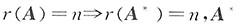 也可逆,且有
也可逆,且有