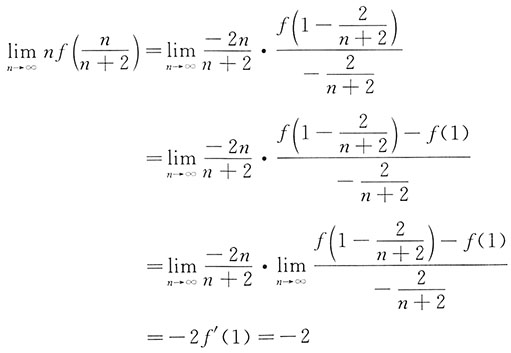一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.3. 把x→0
+时的无穷小量
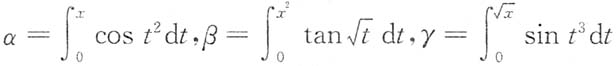
排列起来,使排在后面的是前一个的高阶无穷小量,则正确的排列次序是______
- A.α,β,γ.
- B.α,γ,β.
- C.β,α,γ.
- D.β,γ,α.
A B C D
B
[解析] 解法1 因
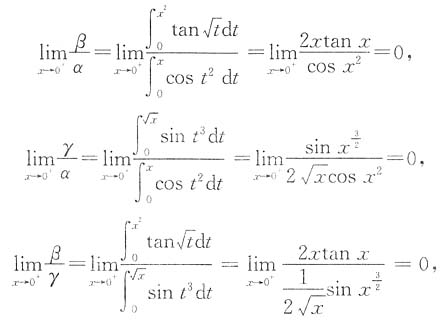
所以γ是较α高阶的无穷小量,β是较γ高阶的无穷小量,即选项B正确.
解法2 α,β,γ阶数的高低次序与它们的导数α',β',γ'阶数的高低次序是一致的,现在考查α'=cosx
2,β'=tanx·2x,
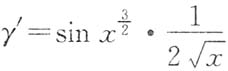
,显然看出由低到高的次序是α',γ',β',则α,β,γ阶数由低到高的次序是α,γ,β,选B.
若是想到利用“变限积分的等价代换”,则本题会更简单,留给读者自练.
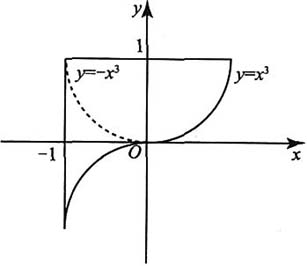
4. 如图所示,连续函数y=f(x)在区间[-3,-2],[2,3]上的图形分别是直径为1的上、下半圆周,在区间[-2,0],[0,2]上的图形分别为直径为2的上、下半圆周.设
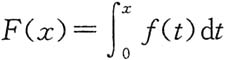
,则下列结论正的是______
A.
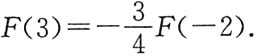
B.
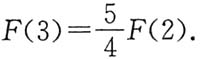
C.
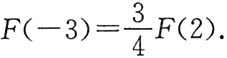
D.
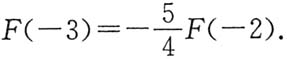
A B C D
C
[解析] 由所给条件,f(x)为x的奇函数,故F(x)为x的偶函数,所以F(-3)=F(3).再利用定积分的几何意义,用半圆面积表示所要计算的定积分,于是有
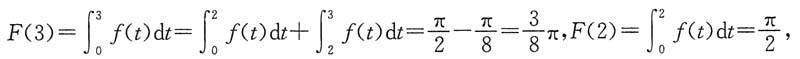
所以
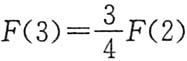
,选C.
6. 设A是三阶可逆矩阵,交换A的第1列和第2列得到B,A
*,B
*分别是A,B的伴随矩阵,则B
*可由______.
- A.A*的第1列与第2列互换得到
- B.A*的第1行与第2行互换得到
- C.-A*的第1列与第2列互换得到
- D.-A*的第1行与第2行互换得到
A B C D
D
[考点] 矩阵
[解析] 应选D.交换A的第1列和第2列得到B,即B=AE
12,其中
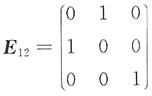
,则|B|=|AE
12|=|A||E
12|=-|A|≠0,故B可逆,且
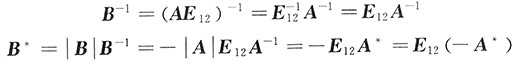
故B
*可由-A
*的第1行与第2行互换得到.
8. 设函数f(x)有二阶连续导数,且
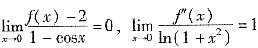
,则______。
- A.(0,f(0))为曲线y=f(x)的拐点
- B.x=0不是极值点,(0,f(0))并不是拐点
- C.x=0为f(x)的极大值点
- D.x=0为f(x)的极小值点
A B C D
D
[考点] 极值及拐点的判定与应用。
[解析] 由
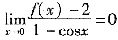
,知f(0)=2,f'(0)=0。又由
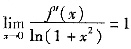
,知在x=0的某邻域内
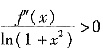
,于是f"(x)>0,可知在点x=0处f(x)取极小值。
三、解答题(本大题共70分.解答应写出文字说明、证明过程或演算步骤.)已知A,B均是2×4矩阵,其中
Ax=0有基础解系α1=(1,1,2,1)T,α2=(0,-3,1,0)T;
Bx=0有基础解系β1=(1,3,0,2)T,β2=(1,2,-1,a)T.1. 求矩阵A;
解:记C=(α
1,α
2),则有AC=A(α
1,α
2)=0,得C
TA
T=0,即A
T的列向量(即A的行向量)是C
Tx=0的解向量.
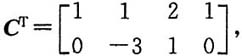
解得C
Tx=0的基础解系为ξ
1=(1,0,0,-1)
T,ξ
2=(-7,1,3,0)
T.
故
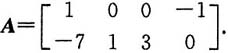
2. 若Ax=0和Bx=0有非零公共解,求参数a的值及公共解.
解:若Ax=0和Bx=0有非零公共解,则非零公共解既可由α
1,α
2线性表出,也可由β
1,β
2线性表出,设公共解为
η=x
1α
1+x
2α
2=x
3β
1+x
4β
2.
于是 x
1α
1+x
2α
2-x
3β
1-x
4β
2=0. (*)
对(α
1,α
2,-β
1,-β
2)作初等行变换,
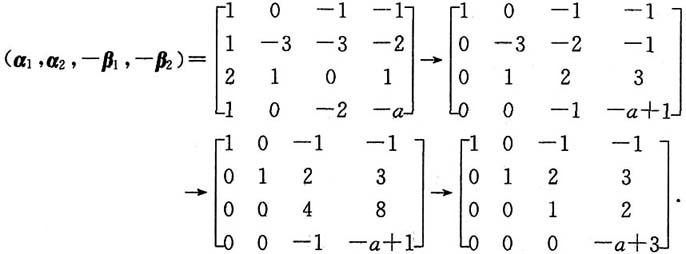
当a=3时,方程组(*)有非零解k(-1,1,-2,1)
T.此时Ax=0和Bx=0的非零公共解为
η=k(-α
1+α
2)=k(-1,-4,-1,-1)
T=k
1(1,4,1,1)
T,
其中k
1是任意非零常数.
或
η=k(-2β
1+β
2)=k
2(1,4,1,1)
T,
其中k
2是任意非零常数.
3. 设f(x)在[x
1,x
2]上可导,且0<x
1<x
2,证明:在(x
1,x
2)内至少存在一个ξ,使
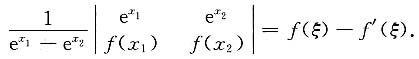
证:令F(x)=e
-xf(x),G(x)=e
-x.由柯西定理,
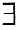
ξ∈(x
1,x
2),使得
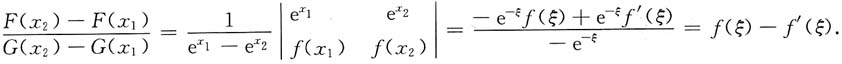
4.
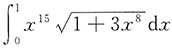
.
解:设1+3x
8=t,则dt=24x
7dx,
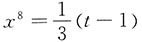
.于是
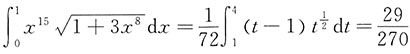
[考点] 不定积分、定积分、反常积分
5. 设函数f(x)在点a处可导,且f(a)≠0,求
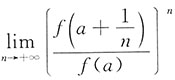
.
解:f(x)=f(a)+f'(a)(x-a)+o(x-a),令
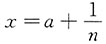
,则
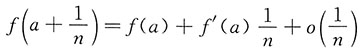
记
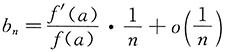
,则
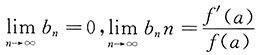
所以原极限即为
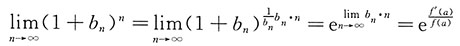
[考点] 连续、导数、微分(Ⅱ)
6. 实系数三元多项式f(x,y,z)=x
3+y
3+z
3-3xyz有没有一次因式?如果有,找出各因式.
解:
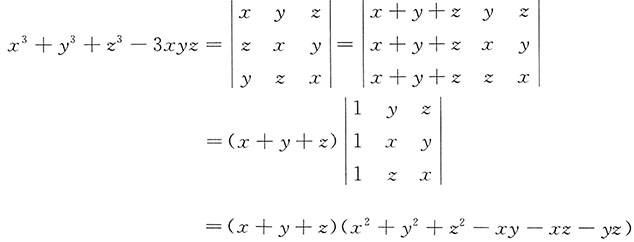
因此f(x,y,z)有一个一次因式(x+y+z).
[考点] 行列式
7. 设曲线y=f(x)和y=x
2-x在点(1,0)处有公共的切线,求
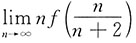
.
解:由题意f'(1)=(x
2-x)'|
x=1=1,从而
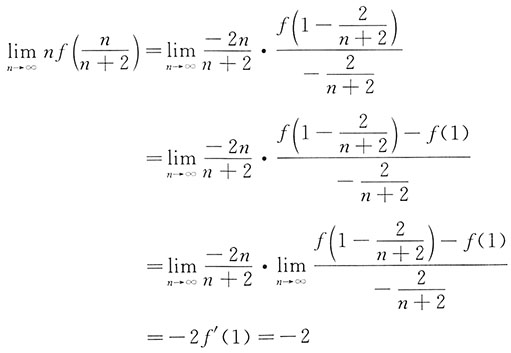
[考点] 一元函数微积分
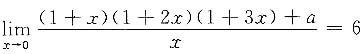 ,则a的值为______
,则a的值为______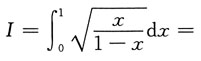 ______
______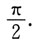
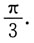
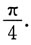

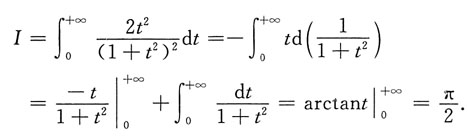
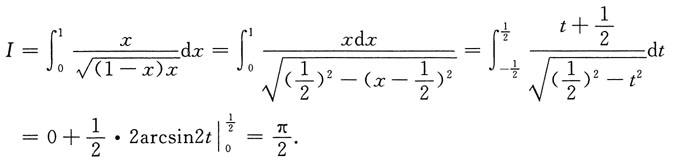
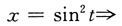
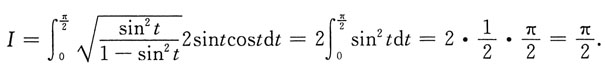
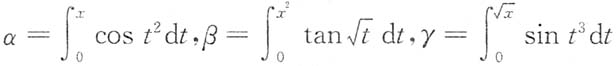 排列起来,使排在后面的是前一个的高阶无穷小量,则正确的排列次序是______
排列起来,使排在后面的是前一个的高阶无穷小量,则正确的排列次序是______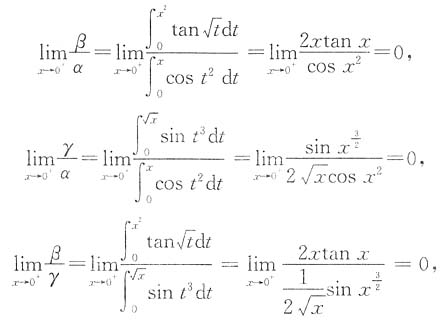
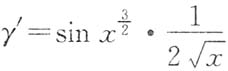 ,显然看出由低到高的次序是α',γ',β',则α,β,γ阶数由低到高的次序是α,γ,β,选B.
,显然看出由低到高的次序是α',γ',β',则α,β,γ阶数由低到高的次序是α,γ,β,选B.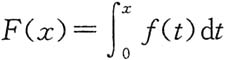 ,则下列结论正的是______
,则下列结论正的是______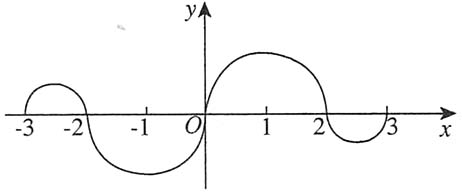
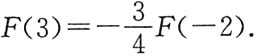
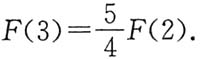
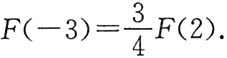
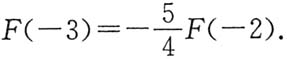
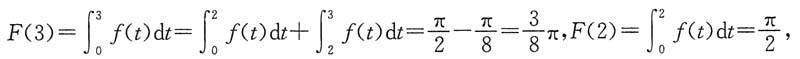
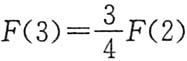 ,选C.
,选C.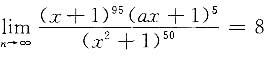 ,则a的值为______
,则a的值为______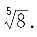
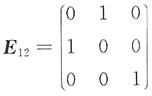 ,则|B|=|AE12|=|A||E12|=-|A|≠0,故B可逆,且
,则|B|=|AE12|=|A||E12|=-|A|≠0,故B可逆,且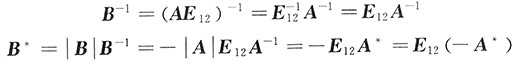
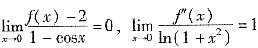 ,则______。
,则______。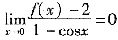 ,知f(0)=2,f'(0)=0。又由
,知f(0)=2,f'(0)=0。又由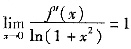 ,知在x=0的某邻域内
,知在x=0的某邻域内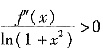 ,于是f"(x)>0,可知在点x=0处f(x)取极小值。
,于是f"(x)>0,可知在点x=0处f(x)取极小值。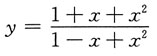 的麦克劳林公式中x4项的系数是______.
的麦克劳林公式中x4项的系数是______.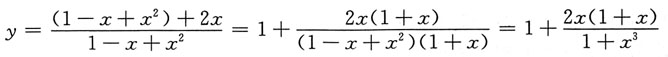
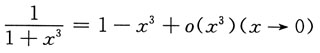 得
得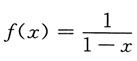 的泰勒公式,将y按变量x的正整数幂展开到含x4项为此,则有
的泰勒公式,将y按变量x的正整数幂展开到含x4项为此,则有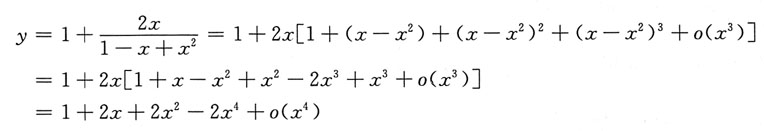
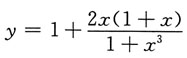 的麦克劳林公式中x4项的系数等同于
的麦克劳林公式中x4项的系数等同于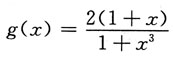 的麦克劳林公式中x3项的系数.可利用求乘积的n阶导数公式,求出g(3)(0),然后求得x3项系数.
的麦克劳林公式中x3项的系数.可利用求乘积的n阶导数公式,求出g(3)(0),然后求得x3项系数.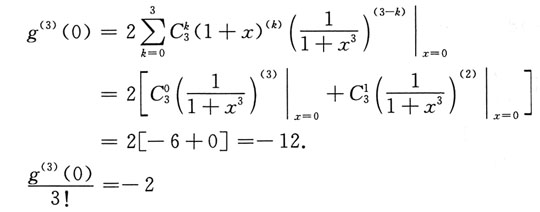
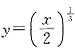
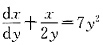 ,这是一阶线性微分方程,其通解为
,这是一阶线性微分方程,其通解为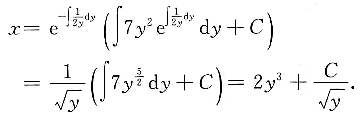
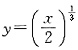 .
.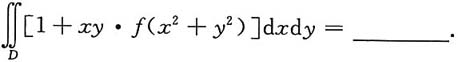

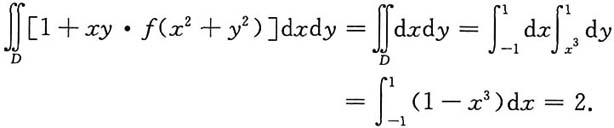
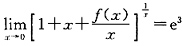 ,则
,则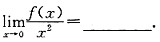
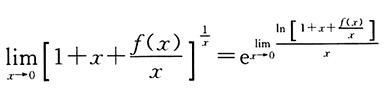 ,由题意得
,由题意得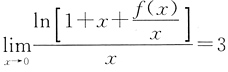 .
.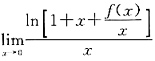 存在,
存在,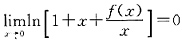 ,故当x→0时,
,故当x→0时,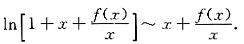
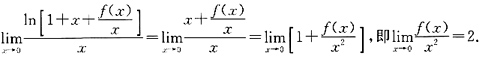
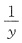 ),其中函数f(u)可微,则
),其中函数f(u)可微,则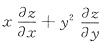 =______.
=______.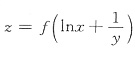 对x求导,得
对x求导,得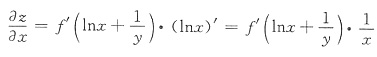
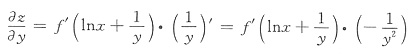
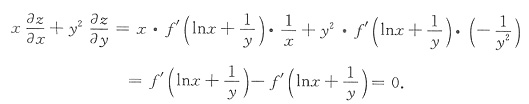
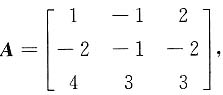 则A-1=______,(A*)-1=______,[(-2A)*]-1=______.
则A-1=______,(A*)-1=______,[(-2A)*]-1=______.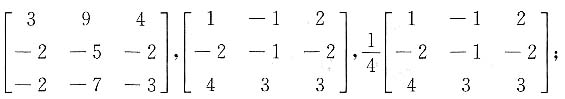
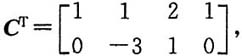
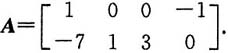

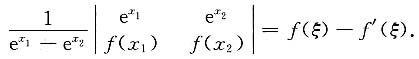
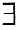 ξ∈(x1,x2),使得
ξ∈(x1,x2),使得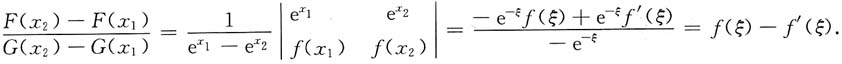
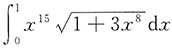 .
.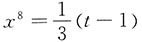 .于是
.于是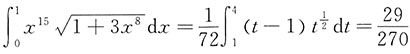
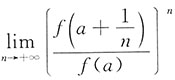 .
.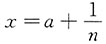 ,则
,则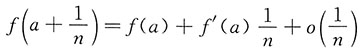
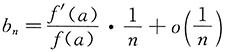 ,则
,则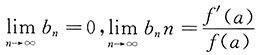
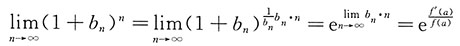
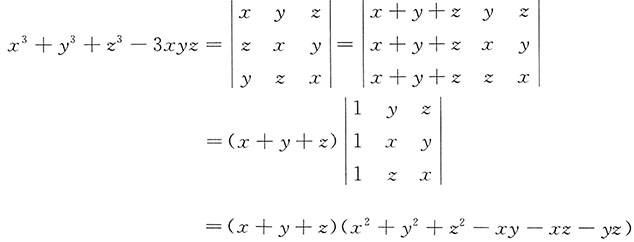
 .
.