要想解决本题的问题，最简单的方法就是使用四重遍历，对所有可能的数对，判断是否满足题目要求，如果满足，那么打印出来，但是这种方法的时间复杂度为O(n⁴)，很显然算法效率太低，不满足题目要求。
   下面介绍另外一种方法——Hash法，该方法的主要思路为：以数对为单位进行遍历，在遍历过程中，把数对和数对的值存储在哈希表中(键为数对的和，值为数对)，当遍历到一个键值对，如果它的和在哈希表中已经存在，那么就找到了满足条件的键值对。
   下面使用HashMap为例给出实现代码：
   //用来存储数对
   public class Pair
   {
   public int First{get; set;}
   

   public int Second {get; set;}
   public Pair(int first, int second)
   {
   this.First=first;
   this.Second=second;
   }
   }
   

   public class ArrayElements
   {
   bool findPairs(int[]arr)
   {
   //键为数对的和, 值为数对
   Dictionary＜int, Pair＞ sumPair=new Dictionary＜int, Pair＞();
   int n=arr.Length;
   

   //遍历数组中所有可能的数对
   for(int i=0; i＜n; ++i)
   {
   for(int j=i+1;j＜n;++j)
   {
   //如果这个数对的和在map中没有, 则放入map中
   int sum= rr[i]+arr[j];
   if(!sumPair.ContainsKey(sum))
   sumPair.Add(sum, new Pair(i, j));
   //map中已经存在与sum相同的数对了, 找出来并打印出来
   else
   {
   //找出已经遍历过的并存储在map中和为sum的数对
   Pair p=sumPair[sum];
   Console.WriteLine("("+arr[p.First]+","+arr[p.Second]+"),("+arr[i]+","+arr[i]+")");
   return true;
   }
   }
   }
   return false;
   }
   

   public static void Main(String[] args)
   {
   int[] arr={3,4,7,10, 20,9,8};
   ArrayElements a=new ArrayElements();
   a.findPairs(arr);
   }
   }
   程序的运行结果为
   (3,8),(4,7)
   算法性能分析：
   因为算法使用了双重循环，所以这个算法的时间复杂度为O(n²)。而HashMap的插入与查找操作实际的时间复杂度为O(l)。

[考点] 如何从数组中找出满足a+b=c+d的两个数对

二叉树的公式：n=n0+n1+n2=n0+n1+(n0-1)=2*n0+n1-1。而在完全二叉树中，n1只能取0或1。若n1=1，则2*n0=1001，可推出n0为小数，不符合题意；若n1=0，则2*n0-1=1001，则n0=501。所以，答案为501。

[考点] 二叉树基础知识

根据二叉树的性质，具有n个结点的完全二叉树的深度为log₂ⁿ+1，因此，含有61个结点的完全二叉树的高度为log₂⁶¹+1，即应该为6层。所以，答案为6。

[考点] 二叉树基础知识

在一棵树中，除了根结点之外，每一个结点都有一条入边，因此，总边数应该是100-1，即99条。所以，答案为99。

[考点] 二叉树基础知识

如果要把一个有序的整数数组放到二叉树中，那么所构造出来的二叉树必定也是一棵有序的二叉树。鉴于此，实现思路为：取数组的中间元素作为根结点，将数组分成两部分，对数组的两部分用递归的方法分别构建左右子树。如下图所示。
   
   如上图所示，首先取数组的中间结点6作为二叉树的根结点，把数组分成左右两部分，然后对于数组的左右两部分子数组分别运用同样的方法进行二叉树的构建，例如，对于左半部分子数组，取中间结点3作为树的根结点，再把数组分成左右两部分。以此类推，就可以完成二叉树的构建，实现代码如下：
   public class Test
   {
   //
   //方法功能: 把有序数组转换为二叉树
   //输入参数: arr:数组
   //返回值: 转换后的树的根结点
   //
   public static BiTNode Arraytotree(int[] arr, int start, int end)
   {
   BiTNode root=null;
   if(end＞=start)
   {
   root=new BiTNode();
   int mid=(start+end+1)/2;
   //树的根结点为数组中间的元素
   root.Data=arr[mid];
   //通过递归法用左半部分数组构造root的左子树
   root.Lchild=Arraytotree(arr, start, mid-1);
   //通过递归法用右半部分数组构造root的右子树
   root.Rchild=Arraytotree(arr, mid+1,end);
   }
   else
   {
   root=null;
   }
   return root;
   }
   

   //用中序遍历的方式打印出二叉树结点的内容
   public static void PrintTreeMidOrder(BiTNode root)
   {
   if(root==null)return;
   //遍历root结点的左子树
   if(root.Lchild!=null)
   PrintTreeMidOrder(root.Lchild);
   //遍历root结点
   Console.Write(root.Data+" ");
   //遍历root结点的右子树
   if(root.Rchild!=null)
   PrintTreeMidOrder(root.Rchild);
   }
   

   public static void Main(String[] args)
   {
   int[] arr={1,2,3,4,5,6,7,8,9,10};
   Console.Write("数组:");
   for(int i=0;i＜arr.Length; i++)
   Console.Write(arr[i]+" ");
   Console.WriteLine();
   BiTNode root;
   root=Arraytotree(arr, 0, arr.Length -1);
   Console.Write("转换成树的中序遍历为:");
   PrintTreeMidOrder(root);
   Console.WriteLine();
   }
   }
   程序的运行结果为
   数组：1 2 3 4 5 6 7 8 9  10
   转换成树的中序遍历为：1 2 3 4 5 6 7 8 9 10
   算法性能分析：
   由于这个方法只遍历了一遍数组，因此，算法的时间复杂度为O(n)，其中，n表示的是数组长度。

[考点] 如何把一个有序整数数组放到二叉树中

为了实现对二叉树的层序遍历，就要求在遍历一个结点的同时记录下它的孩子结点的信息，然后按照这个记录的顺序来访问结点的数据，在实现的时候可以采用队列来存储当前遍历到的结点的子结点，从而实现二叉树的层序遍历，遍历过程如下图所示。
   
   在上图中，1)首先把根结点1放到队列里而，然后开始遍历。2)队列首元素(结点1)出队列，同时它的子结点2和3进队列；3)接着出队列的结点为2，同时把它的孩子结点4和5放到队列里，以此类推就可以实现对二叉树的层序遍历。
   实现代码如下：
   public class Test
   {
   //
   //方法功能: 用层序遍历的方式打印出二叉树结点的内容
   //输入参数: root:二叉树根结点
   //
   public static void PrintTreeLayer(BiTNode root)
   {
   if (root==null) return;
   BiTNode p;
   Queue＜BiTNode＞ queue=new Queue＜BiTNode＞();
   //二叉树根结点进队列
   queue.Enqueue(root);
   while(queue.Count()＞0)
   {
   p=queue.Dequeue();
   //访问当前结点
   Console.Write(p.Data+"");
   //如果这个结点的左孩子不为空则入队列
   if(p.Lchild!=null)
   queue.Enqueue(p.Lchild);
   //如果这个结点的右孩子不为空则入队列
   if(p.Rchild!=null)
   queue.Enqueue(p.Rchild);
   }
   }
   public static void Main(String[] args)
   {
   int[] arr={1,2,3,4,5,6,7,8,9,10};
   BiTNode root=Arraytotree(arr,0,arr.Length-1)；
   Console.Write("树的层序遍历结果为：");
   PrintTreeLayer(root);
   }
   }
   程序的运行结果为
   树的层序遍历结果为：6 3 9 2 5 8 10 1 4 7
   算法性能分析：
   在二叉树的层序遍历过程中，对树中的各个结点只进行了一次访问，因此，时间复杂度为O(n)，此外，这个方法还使用了队列来保存遍历的中间结点，所使用队列的大小取决于二叉树中每一层中结点个数的最大值。具有N个结点的完全二叉树的深度为h=log₂ⁿ+1。而深度为h的这一层最多的结点个数为2^h-1=n/2。也就是说队列中可能的最多的结点个数为n/2。因此，这种算法的空间复杂度为O(n)。
   引申：用空间复杂度为O(l)的算法来实现层序遍历。
   上面介绍的算法的空间复杂度为O(n)，显然不满足要求。通常情况下，提高空间复杂度都是要以牺牲时间复杂度作为代价的。对于本题而言，主要的算法思路为：不使用队列来存储每一层遍历到的结点，而是每次都会从根结点开始遍历。把遍历二叉树的第k层的结点，转换为遍历二叉树根结点的左右子树的第k-1层结点。算法如下所示：
   int PrintAtLevel(BiTNode root, int level)
   {
   if(root==null||level＜0)
   return 0;
   else if (level==0)
   {
   Console.WriteLine(root.Data);
   return 1;
   }
   else
   {
   //
   //把打印根结点level层的结点转换为求解根结点的孩子结点的level-1
   //层的结点。
   //
   return PrintAtLevel(root.Lchild, level-1)+ PrintAtLevel(root.Rchild, level-1);
   }
   }
   通过上述算法，可以首先求解出二叉树的高度h，然后调用上面的函数h次就可以打印出每一层的结点。

[考点] 如何从顶部开始逐层遍历二叉树结点数据

要求一棵二叉树的最大子树和，最容易想到的办法就是针对每棵子树，求出这棵子树中所有结点的和，然后从中找出最大值。恰好二叉树的后序遍历就能做到这一点。在对二叉树进行后序遍历的过程中，如果当前遍历的结点的值与其左右子树和的值相加的结果大于最大值，则更新最大值。如下图所示：
   
   在上面这个图中，首先遍历结点-1，这个子树的最大值为-1，同理，当遍历到结点9时，子树的最大值为9，当遍历结点3的时候，这个结点与其左右孩子结点值的和(3-1+9=11)大于最大值9。因此，此时最大的子树为以3为根结点的子树，以此类推，直到遍历完整棵树为止。实现代码如下：
   public class Test
   {
   private static int maxSum=int.MinValue;
   //
   //方法功能: 求最大子树
   //输入参数: root:根结点; maxSum最大子树结点的和,
   //    maxRoot指向最大子树的根结点
   //返回值: 以root为根节点子树所有结点的和
   //
   public static int FindMaxSubTree(BiTNode root, BiTNode maxRoot)
   {
   if(root==null)
   {
   return 0;
   }
   //求root左子树所有结点的和
   int lmax=FindMaxSubTree(root.Lchild, maxRoot);
   //求root右子树所有结点的和
   int rmax=FindMaxSubTree(root.Rchild, maxRoot);
   int sum=lmax+rmax+root.Data;
   //以root为根的子树的和大于前面求出的最大值
   if(sum＞maxSum)
   {
   maxSum=sum;
   maxRoot.Data=root.Data;
   }
   //返回以root为根结点的予树的所有结点的和
   return sum;
   }
   

   //
   //方法功能: 构造二叉树
   //返回值: 返回新构造的二叉树的根结点
   //
   public static BiTNode constructTree()
   {
   BiTNode root=new BiTNode();
   BiTNode node1=new BiTNode();
   BiTNode node2=new BiTNode();
   BiTNode node3=new BiTNode();
   BiTNode node4=new BiTNode();
   root.Data=6;
   node1.Data=3;
   node2.Data=-7;
   node3.Data=-1;
   node4.Data=9;
   root.Lchild=node1;
   root.Rchild=node2;
   node1.Lchild=node3;
   node1.Rchild=node4;
   node2.Lchild=node2.Rchild=node3.Lchild=node3.Rchild=
   node4.Lchild=node4.Rchild=null;
   return root;
   }
   

   public static void Main(String[] args)
   {
   //构造二叉树
   BiTNode root=constructTree();
   BiTNode maxRoot=new BiTNode();//最大子树的根节点
   FindMaxSubTree(root, maxRoot);
   Console.WriteLine("最大子树和为: "+maxSum);
   Console.WriteLine("对应子树的根结点为: "+maxRoot.Data);
   }
   }
   程序的运行结果为
   最大子树和为：11
   对应子树的根结点为：3
   算法性能分析：
   这个算法与二叉树的后序遍历有相同的时间复杂度，即为O(n)，其中，n为二叉树的结点个数。

[考点] 如何求一棵二叉树的最大子树的和

如果两棵二叉树root1、root2相等，那么root1与root2结点的值相同，同时它们的左右孩子也有着相同的结构，并且对应位置上结点的值相等，即root1.data==root2.data，并且root1的左子树与root2的左子树相等，并且root1的右子树与root2的右子树相等。根据这个条件，可以非常容易地写出判断两棵二叉树是否相等的递归算法。实现代码如下：
   public class Test
   {
   //
   //方法功能: 判断四个二叉树是否相等
   //参数: root1与root2分别为两个二叉树的根结点
   //返回值: true:如果两棵树相等, 否则返回false
   //
   public static boolIsEqual(BiTNode root1, BiTNode root2)
   {
   if(root1==null＆＆root2==null)
   return true;
   if(root1==null ＆＆ root2!=null)
   return false;
   if(root1!=null ＆＆ root2==null)
   return false;
   if(root1.Data==root2.Data)
   return isEqual(root1.Lchild, root2.Lchild) ＆＆ isEqual(root1.Rchild, root2.Rchild);
   else
   return false;
   }
   public static void Main(String[] args)
   {
   BiTNode root1=ConstructTree();
   BiTNode root2=ConstructTree();
   bool equal=IsEqual(root1, root2);
   if(equal)
   Console.WriteLine("这两裸树相等");
   else
   Console.WriteLine("这两棵树不相等");
   }
   }
   程序的运行结果为
   这两棵树相等
   算法性能分析：
   这个算法对两棵树只进行了一次遍历，因此，时间复杂度O(n)。此外，这个算法没有申请额外的存储空间。

[考点] 如何判断两棵二叉树是否相等

由于转换后的双向链表中结点的顺序与二叉树的中序遍历的顺序相同，因此，可以对二叉树的中序遍历算法进行修改，通过在中序遍历的过程中修改结点的指向来转换成一个排序的双向链表。实现思路如下图所示：假设当前遍历的结点为root，root的左子树已经被转换为双向链表(如下图(1)所示)，使用两个变量pHead与pEnd分别指向链表的头结点与尾结点。那么在遍历root结点的时候，只需要将root结点的lchild指向pEnd，把pEnd的rchild(右)指向root；此时root结点就被加入到双向链表里了，因此，root变成了双向链表的尾结点，如图(2)所示。对于所有的结点都可以通过同样的方法来修改结点的指向。因此，可以采用递归的方法来求解，在求解的时候需要特别注意递归的结束条件以及边界情况(例如双向链表为空的时候)。
   
   实现代码如下：
   public class Test
   {
   private static BiTNode pHead=null;//双向链表头结点
   private static BiTNode pEnd=null;//双向链表尾结点
   

   //
   //方法功能: 把二叉树转换为双向列表
   //输入参数: root:二叉树根结点
   //
   public static void inOrderBSTree(BiTNode root)
   {
   if(null==root)
   {
   return;
   }
   //转换root的左子树
   inOrderBSTree(root.Lchild);
   

   root.Lchild=pEnd;//使当前结点的左指针指向双向链表中最后一个结点
   if(null==pEnd)
   {//双向列表为空, 当前遍历的结点为双向链表的头结点
   pHead=root;
   }
   else
   {//使双向链表中最后一个结点的右指针指向当前结点
   pEnd.Rchild=root;
   }
   pEnd=root;//将当前结点设为双向链表中最后一个结点
   

   //转换root的右子树
   inOrderBSTree(root.Rchild);
   }
   

   public static void Main(String[] args)
   {
   int[] arr={1,2,3,4,5,6,7};
   BiTNode root;
   root=Arraytotree(arr,0, arr.Length-1);
   inOrderBSTree(root);
   BiTNode cur;
   Console.Write("转换后双向链表正向遍历:");
   for(cur=pHead; cur!=null; cur=cur.Rchild)
   Console.Write(cur.Data+"");
   Console.WriteLine();
   Console.Write("转换后双向链表逆向遍历:");
   for(cur=pEnd; cur!=null; cur=cur.Lchild)
   Console.Write(cur.Data+" ");
   }
   }
   程序的运行结果为
   转换后双向链表正向遍历：1 2 3 4 5 6 7
   转换后双向链表逆向遍历：7 6 5 4 3 2 1
   算法性能分析：
   这个算法与二叉树的中序遍历有着相同的时间复杂度O(n)。此外，这个算法只用了两个额外的变量pHead与pEnd来记录双向链表的首尾结点。因此，空间复杂度为O(l)。

[考点] 如何把二叉树转换为双向链表

二元查找树的特点是：对于任意一个结点，它的左子树上所有结点的值都小于这个结点的值，它的右子树上所有结点的值都大于这个结点的值。根据它的这个特点以及二元查找树后序遍历的特点，可以看出，这个序列的最后一个元素一定是树的根结点(上图中的结点4)，然后在数组中找到第一个大于根结点4的值5，那么结点5之前的序列(1,3,2)对应的结点一定位于结点4的左子树上，结点5(包含这个结点)后面的序列一定位于结点4的右子树上(也就是说结点5后面的所有值都应该大于或等于4)。对于结点4的左子树遍历的序列{1,3,2}以及右子树的遍历序列{5,7,6}可以采用同样的方法来分析，因此，可以通过递归方法来实现，实现代码如下：
   public class Test
   {
   //
   //方法功能: 判断一个数组是否是二元查找树的后续遍历序列
   //输入参数: arr:数组;
   //返回值: true:是, 否则返回false
   //
   public static bool IsAfterOrder(int[] arr, int start, int end)
   {
   if(arr==null)
   {
   return false;
   }
   //数组的最后一个结点必定是根结点
   int root=arr[end];
   int i,j;
   //找到第一个大于root的值, 那么前面所有的结点都位于root的左子树上
   for(i=start;i＜end;i++)
   {
   if(arr[i]＞root)
   break;
   }
   //如果序列是后续遍历的序列, 那么从i开始的所有值都应该大于根结点root的值
   for(j=i; j＜end;j++)
   {
   if(arr[j]＜root)
   return false;
   }
   bool left_IsAfterOrder=true;
   bool right_IsAfterOrder=true;
   //判断小于root值的序列是否是某一二元查找树的后续遍历
   if(i＞start)
   left_IsAfterOrder=IsAfterOrder(arr, start,i-1);
   //判断大于root值的序列是否是某一二元查找树的后续遍历
   if(j＜end)
   right_IsAfterOrder=IsAfterOrder(arr,i,end);
   return(left_IsAfterOrder ＆＆ right_IsAfterOrder);
   }
   

   public static void Main(String[] args)
   {
   int[] arr={1,3,2,5,7,6,4};
   bool result=IsAfterOrder(arr,0, arr.Length-1);
   for(int i=0;i＜arr.Length; i++)
   Console.Write(arr[i]+"");
   if(result)
   Console.WriteLine("是某一二元查找树的后续遍历序列");
   else
   Console.WriteLine("不是是某一二元查找树的后续遍历序列");
   }
   }
   程序的运行结果为
   1 3 2 5 7 6 4是某一二元查找树的后序遍历序列
   算法性能分析：
   这个方法对数组只进行了一次遍历，因此，时间复杂度O(n)。

[考点] 如何判断一个数组是否是二元查找树后序遍历的序列

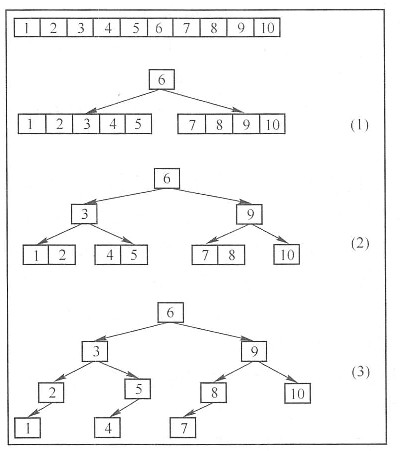
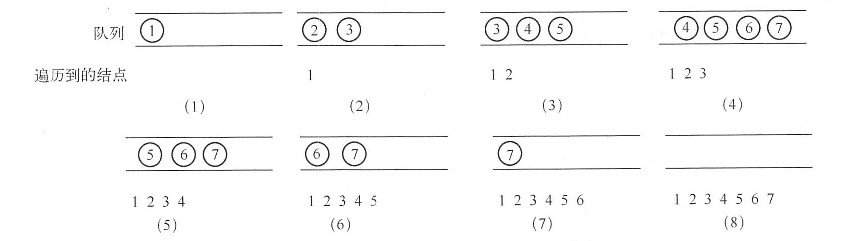
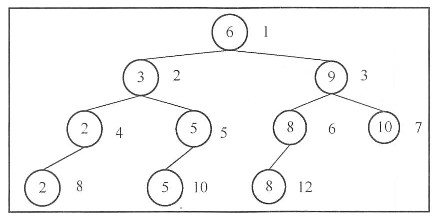
方法一：路径对比法
   对于一棵二叉树，如果知道了从根结点到这两个结点的路径，就可以很容易地找出它们最近的公共父结点。因此，可以首先分别找出从根结点到这两个结点的路径(例如上图中从根结点到结点1的路径为6-＞3-＞2-＞1，从根结点到结点5的路径为6-＞3-＞5)；然后遍历这两条路径，只要是相等的结点都是它们的父结点，找到最后一个相等的结点即为离它们最近的共同父结点，在这个例子中，3就是它们共同的父结点。
   实现代码如下：
   public class Test
   {
   //
   //方法功能: 获取二叉树从根结点root到node结点的路径
   //输入参数: root:根结点; node:二叉树中的某个结点; s: 用来存储路径的栈
   //返回值: node在root的子树上, 或node=root时返回true, 否则返回false
   //
   private static bool getPathFromRoot(BiTNode root, BiTNode node, Stack＜BiTNode＞s)
   {
   if(root==null)
   return false;
   if(root==node)
   {
   s.Push(root);
   return true;
   }
   //
   //如果node结点在root结点的左子树或右子树上,
   //那么root就是node的祖先结点,把它加到栈里
   //
   if(getPathFromRoot(root.Lchild, node,s)||
   getPathFromRoot(root.Rchild, node, s)
   {
   s.Push(root);
   return true;
   }
   return false;
   }
   

   //
   //方法功能: 查找二叉树中两个节点最近的共同父结点
   //输入参数: root:根结点; node1与node2为二叉树中两个结点
   //返回值: node1与node2最近的共同父结点
   //
   public static BiTNode FindParentNode(BiTNode root, BiTNode node1, BiTNode node2)
   {
   Stack＜BiTNode＞stack1=new Stack＜BiTNode＞();//保存从root到node1的路径
   Stack＜BiTNode＞stack2=new Stack＜BiTNode＞();//保存从root到node2的路径
   //获取从root到node1的路径
   getPathFromRoot(root, node1, stack1);
   //获取从root到node2的路径
   getPathFromRoot(root, node2, stack2);
   BiTNode commomParent=null;
   //获取最靠近node1和node2的父结点
   while(stack1.Peek()==stack2.Peek())
   {
   commomParent=stack1.Peek();
   stack1.Pop();
   stack2.Pop();
   }
   return commomParent;
   }
   

   public static void Main(String[] args)
   {
   int[] arr={1,2,3,4,5,6,7,8,9,10};
   BiTNode root;
   root=Arraytotree(arr,0,arr.Length-1);
   BiTNode node1=root.Lchild.Lchild.Lchild;
   BiTNode node2=root.Lchild.Rchild;
   BiTNode res=null;
   res=FindParentNode(root, node1, node2);
   if(res!=null)
   Console.Write(node1.Data+"与"+node2.Data+"的最近公共父结点为: "+res.Data);
   else
   Console.WriteLine("没有公共父结点");
   }
   }
   程序的运行结果为
   1与5的最近公共父结点为：3
   算法性能分析：
   当获取二叉树从根结点root到node结点的路径时，最坏的情况就是把树中所有结点都遍历一遍，这个操作的时间复杂度为O(n)，再分别找出从根结点到两个结点的路径后，找它们最近的公共父结点的时间复杂度也为O(n)，因此，这个算法的时间复杂度为O(n)。此外，这个算法用栈保存了从根结点到特定结点的路径，在最坏的情况下，这个路径包含了树中所有的结点，因此，空间复杂度也为O(n)。
   很显然，这个方法还不够理想。下面介绍另外一种能降低空间复杂度的方法。
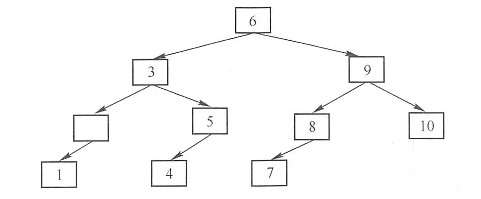
   方法二：结点编号法
   把二叉树看成是一棵完全二叉树(不管实际的二叉树是否为完全二叉树，二叉树中的结点都可以按照完全二叉树中对结点编号的方式进行编号)，下图为对二叉树中的结点按照完全二叉树中结点的编号方式进行编号后的结果，结点右边的数字为其对应的编号。
   
   一个编号为n的结点，它的父亲结点的编号为n/2。假如要求node1与node2的最近的共同父结点，首先把这棵树看成是一棵完全二叉树(不管结点是否存在)，分别求得这两个结点的编号n1，n2。然后每次找出n1与n2中较大的值除以2，直到n1==n2为止，此时n1或n2的值对应结点的编号就是它们最近的共同父结点的编号，接着可以根据这个编号信息找到对应的结点，具体方法为：通过观察二叉树中结点的编号可以发现：首先把根结点root看成1，求root的左孩子编号的方法为把root对应的编号看成二进制，然后向左移一位，末尾补0，如果是root的右孩子，则末尾补1，因此，通过结点位置的二进制码就可以确定这个结点。例如结点3的编号为2(二进制10)，它的左孩子的求解方法为：10，向左移一位末尾补0，可以得到二进制100(十进制4)，位置为4的结点的值为2。从这个特性可以得出通过结点位置信息获取结点的方法，例如要求位置4的结点，4的二进制码为100，由于1代表根结点，接下一个0代表是左子树root.lchild，最后一个0也表示左子树root.lchild.lchild，通过这种方法非常容易根据结点的编号找到对应的结点。实现代码如下：
   class IntRef{
   public int Num {get;set;}
   }
   

   public class Test1
   {
   //
   //方法功能: 找出结点在二叉树中的编号
   //输入参数: root:根结点; node:待查找结点; number: node结点在二叉树中的编号
   //返回值: true:找到该结点的位置, 否则返回false
   //
   private static bool GetNo(BiTNode root, BiTNode node, IntRef number)
   {
   if (root==null)
   return false;
   if(root==node)
   return true;
   int tmp=number.Num;
   number.Num=2*tmp;
   //node结点在root的左子树中, 左子树编号为当前结点编号的2倍
   if(GetNo(root.Lchild, node, number))
   {
   return true;
   //node结点在root的右子树中, 右子树编号为当前结点编号的2倍加1
   }
   else
   {
   number.Num=tmp*2+1;
   return GetNo(root.Rchild, node,number);
   }
   }
   

   //
   //方法功能: 根据结点的编号找出对应的结点
   //输入参数: root根结点; number为结点的编号
   //返回值: 编号为number对应的结点
   //
   private static BiTNode getNodeFromNum(BiFNode root,int number)
   {
   if (root==null||number＜0)
   return null;
   if(number==1)
   return root;
   //结点编号对应二进制的位数(最高位一定为1, 由于根节点代表1)
   int len=(int)(Math.Log(number)/Math.Log(2));
   //去掉根结点表示的1
   number-=1＜＜len;
   for(;len＞0; len--)
   {
   //如果这一位二进制的值为1,
   //那么编号为number的结点必定在当前结点的右子树上
   if(((1＜＜(len-1))＆ number)==1)
   root=root.Rchild;
   else
   root=root.Lchild;
   }
   return root;
   }

   //
   //方法功能： 查找二叉树中两个节点最近的共同父结点
   //输入参数： root:根结点； node1与node2为二叉树中两个结点
   //返回值： node1与node2最近的共同父结点
   //
   public static BiTNode FindParentNode(BiTNode root, BiTNode node1, BiTNode node2)
   {
   IntRef ref1=new IntRef();
   ref1.Num=1;
   IntRef ref2=new IntRef();
   ref2.Num=1;
   GetNo(root, node1, ref1);
   GetNo(root, node2, ref2);
   int num1=ref1.Num;
   int num2=ref2.Num;
   //找出编号为num1和num2的共同父结点
   while(num1!=num2)
   {
   if(num1＞num2)
   num1/=2;
   else
   num2/=2;
   }
   //num1就是它们最近的公共父结点的编号， 通过结点编号找到对应的结点
   return getNodeFromNum(root, num1);
   }
   }
   算法性能分析：
   这个方法的时间复杂度也为O(n)，与方法一相比，在求解的过程中只用了个别的几个变量，因此，空间复杂度为O(l)。
   方法三：后序遍历法
   很多与二叉树相关的问题都可以通过对二叉树的遍历方法进行改装而求解。对于本题而言，可以通过对二叉树的后序遍历进行改编而得到。具体思路为：查找结点node1与结点node2的最近共同父结点可以转换为找到一个结点node，使得node1与node2分别位于结点node的左子树或右子树中。结点1与结点5的最近共同父结点为结点3，因为结点1位于结点3的左予树上，而结点5位于结点3的右子树上。实现代码如下：
   public static BiTNode FindParentNode(BiTNode root, BiTNode node1, BiTNode node2)
   {
   if (null==root||root==node1||root==node2)
   {
   return root;
   }
   BiTNode lchild=FindParentNode(root.Lchild, node1, node2);
   BiTNode rchild=FindParentNode(root.Rchild, node1, node2);
   //root的左子树中没有结点node1和node2,那么一定在root的右子树上
   if(null==lchild)
   {
   return rchild;
   }
   //root的右子树中没有结点node1和node2, 那么一定在root的左子树上
   else if(null==rchild)
   {
   return lchild;
   }
   //node1与node2分别位于root的左子树与右子树上, root就是它们最近的共同父结点
   else
   {
   return root;
   }
   }
   把方法一中的FindParentNode替换为本方法的FindParentNode方法可以得到同样的输出结果。
   算法性能分析：
   这个方法与二叉树的后序遍历方法有着相同的时间复杂O(N)。
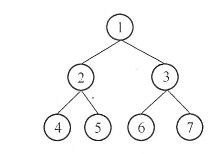
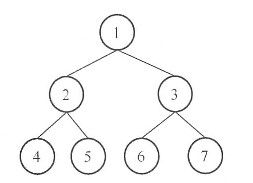
   引申：如何计算二叉树中两个结点的距离
   题目描述：
   在没有给出父结点的条件下，计算二叉树中两个结点的距离。两个结点之间的距离是从一个结点到达另一个结点所需的最小的边数。例如：给出下面的二叉树：
   
   Dist(4,5)=2, Dist(4,6)=4。
   分析与解答：
   对于给定的二叉树root，只要能找到两个结点n1与n2最低的公共父结点parent，那么就可以通过下面的公式计算出这两个结点的距离：
   Dist(n1, n2)=Dist(root, n1)+Dist(root, n2)-2*Dist(root, parent)

[考点] 如何找出排序二叉树上任意两个结点的最近共同父结点