这道题主要考察对递归的理解,可以采用递归的方法来实现。当然也可以使用非递归的方法来实现,但是与递归法相比,非递归法难度增加了很多。下面分别介绍这两种方法。
方法一:递归法 以下以字符串abc为例介绍对字符串进行全排列的方法。具体步骤如下所示:
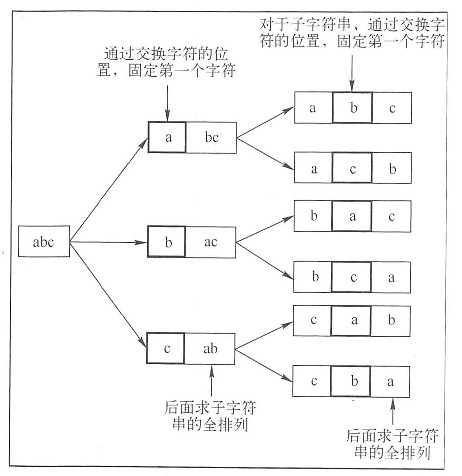
1)首先固定第一个字符a,然后对后面的两个字符b与c进行全排列;
2)交换第一个字符与其后面的字符,即交换a与b,然后固定第一个字符b,接着对后面的两个字符a与c进行全排列;
3)由于第2)步交换了a和b破坏了字符串原来的顺序,因此,需要再次交换a和b使其恢复到原来的顺序,然后交换第一个字符与第三个字符(交换a和c),接着固定第一个字符c,对后面的两个字符a与b求全排列。
在对字符串求全排列的时候就可以采用递归的方式来求解,实现方法如下图所示:
在使用递归方法求解的时候,需要注意以下两个问题:1)逐渐缩小问题的规模,并且可以用同样的方法来求解子问题;2)递归一定要有结束条件,否则会导致程序陷入死循环。本题目递归方法实现代码如下所示:
public class Test
{
//交换字符数组下标为i和j对应的字符
static void Swap(char[] str, int i, int j)
{
char tmp=str[i];
str[i]=str[j];
str[j]=tmp;
}
//
//方法功能:对字符串中的字符进行全排列
//输入参数:str为待排序的字符串,start为待排序的子字符串的首字符下标
//
static void Permutation(char[] str, int start)
{
if (str==null||start<0)
return;
//完成全排列后输出当前排列的字符串
if(start==str.Length-1)
Console.WriteLine(str);
else
{
for(int i=start;i<str.Length;i++)
{
//交换start与i所在位置的字符
Swap(str, start,i);
//固定第一个字符,对剩余的字符进行全排列
Permutation(str, start+1);
//还原start与i所在位置的字符
Swap(str, start,i);
}
}
}
static void Permutation(String s)
{
char[] str=s.ToCharArray();
Permutation(str, 0);
}
public static void Main(String[] args)
{
String s="abc";
Permutation(s);
Console.Read();
}
}
程序的运行结果为
abc acb bac bca cba cab
算法性能分析: 假设这个算法需要的基本操作数为f(n),那么f(n)=n*f(n-1)=n*(n-1)*f(n-2)...=n!。所以,算法的时间复杂度为O(n!)。算法在对字符进行交换的时候用到了常量个指针变量,因此,算法的空间复杂度为O(l)。
方法二:非递归法 递归法比较符合人的思维,因此,算法的思路以及算法实现都比较容易。下面介绍另外一种非递归的方法。算法的主要思想为:从当前字符串出发找出下一个排列(下一个排列为大于当前字符串的最小字符串)。
通过引入一个例子来介绍非递归算法的基本思想:假设要对字符串“12345”进行排序。第一个排列一定是“12345”,依此获取下一个排列:“12345”->“12354”->“12435”->“12453”->“12534”->“12543”->“13245”->…。从“12543”->“13245”可以看出找下一个排列的主要思路为:1)从右到左找到两个相邻递增(从左向右看是递增的)的字符,例如“12543”,从右到左找出第一个相邻递增的子串为“25”;记录这个小的字符的下标为pmiri;2)找出pmin后面的比它大的最小的字符进行交换,在本例中‘2’后面的子串中比它大的最小的字符为‘3’,因此,交换‘2’和‘3’得到字符串“13542”;3)为了保证下一个排列为大于当前字符串的最小字符串,在第2)步中完成交换后需要对pmin后的子串重新组合,使其值最小,只需对pmin后面的字符进行逆序即可(因为此时pmin后面的子字符串中的字符必定是按照降序排列,逆序后字符就按照升序排列了),逆序后就能保证当前的组合是新的最小的字符串;在这个例子中,上一步得到的字符串为“13542”,pmin指向字符‘3’,对其后面的子串“542”逆序后得到字符串“13245”;4)当找不到相邻递增的子串时,说明找到了所有的组合。
需要注意的是,这种方法适用于字符串中的字符是按照升序排列的情况。因此,非递归方法的主要思路为:1)首先对字符串进行排序(按字符进行升序排列);2)依次获取当前字符串的下一个组合直到找不到相邻递增的子串为止。实现代码如下:
public class Test
{
//交换字符数组下标为i和j对应的字符
private static void Swap(char[] str, int i, int j)
{
char tmp=str[i];
str[i]=str[j];
str[j]=tmp;
}
//
//方法功能: 翻转字符串
//输入参数: begin与end分别为字符串的第一个字符与最后一个字符的下标
//
private static void Reverse(char[] str, int begin, int end)
{
for(int i=begin, j=end; i<j; i++,i--)
Swap(str,i,j);
}
//
//方法功能: 根据当前字符串的获取下一个组合
//输入参数: str: 字符数组
//返回值: 还有下—个组合返回true, 否则返回false
//
private static bool getNextPermutation(char[] str)
{
int end=str.Length-1;//字符串最后一个字符的下标
int cur=end;//用来从后向前遍历字符串
int suc=0;//cur的后继
int tmp=0;
while(cur!=0)
{ //从后向前开始遍历字符串
suc=cur;
cur--;
if(str[cur]<str[suc])
{ //相邻递增的字符, cur指向较小的字符
//找出cur后面最小的字符tmp
tmp=end;
while(str[tmp]<str[cur])
--tmp;
//交换cur与tmp
Swap(str, cur, tmp);
//把cur后面的子字符串进行翻转
Reverse(str, suc, end);
return true;
}
}
return false;
}
//
//方法功能: 获取字符串中字符的所有组合
//输入参数: str: 字符数组
//
public static void Permutation(String s)
{
if(s==null||s.Length<1)
{
Console.WriteLine("参数不合法");
}
char[] str=s.ToCharArray();
Array.Sort(str);//升序排列字符数组
do
{
Console.WriteLine(str);
}
while (getNextPermutation(str));
}
public static void Main(String[] args)
{
String s="abc";
Permutation(s);
}
}
程序的运行结果为
abc acb bac bca cab cba
算法性能分析: 首先对字符串进行排序的时间复杂度为O(n
2),接着求字符串的全排列,由于长度为n的字符串全排列个数为n!,因此,Permutation函数中的循环执行的次数为n!,循环内部调用函数getNextPermutation,getNextPermutation函数内部用到了双重循环,因此,它的时间复杂度为O(n
2)。所以,求全排列算法的时间复杂度为O(n!*n
2)。
引申:如何去掉重复的排列 分析与解答: 当字符串中没有重复的字符的时候,它的所有组合对应的字符串也就没有重复的情况,但是当字符串中有重复的字符的时候,例如“baa”,此时如果按照上面介绍的算法求全排列的时候就会有重复的字符串。
由于全排列的主要思路为:从第一个字符起每个字符分别与它后面的字符进行交换:例如:对于“baa”,交换第一个与第二个字符后得到“aba”,再考虑交换第一个与第三个字符后得到“aab”,由于第二个字符与第三个字符相等,会导致这两种交换方式对应的全排列是重复的(在固定第一个字符的情况下它们对应的全排列都为“aab”和“aba”)。从上面的分析可以看出去掉重复排列的主要思路为:从第一个字符起每个字符分别与它后面非重复出现的字符进行交换。在递归方法的基础上只需要增加一个判断字符是否重复的函数即可,实现代码如下:
public class Test
{
//方法功能: 交换字符数组下标为i和j对应的字符
private static void Swap(char[] str, int i, int j)
{
char tmp=str[i];
str[i]=str[j];
str[j]=tmp;
}
//
//函数功能: 判断[begin,end)区间中子否有字符与*end相等
//输入参数: begin和end为指向字符的指针
//返回值: true:如果有相等的字符, 负责返回false
//
private static bool IsDuplicate(char[] str, int begin, int end)
{
for (int i=begin;i<end;i++)
{
if (str[i]==str[end])
return false;
}
return true;
}
//
//函数功能: 对字符串中的字符进行全排列
//输入参数: str为待排序的字符串,start为待排序的子字符串的首字符下标
//
public static void Permutation(char[] str, int stalt)
{
if(str==null||start<0)
return;
//完成全排列后输出当前排列的字符串
if(start==str.Length-1)
Console.Write(new String(str)+"");
else
{
for (int i=start;i<str.Length; i++)
{
if(!IsDuplicate(str, start,i))
continue;
//交换start与i所在位置的字符
Swap(str, start,i);
//固定第一个字符, 对剩余的字符进行全排列
Permutation(str, start+1);
//还原start与i所在位置的字符
Swap(str, start,i);
}
}
}
public static void Permutation(String s)
{
char[] str=s.ToCharArray();
Permutation(str, 0);
}
public static void Main(String[] args)
{
String s="aba";
Permutation(s);
}
}
程序的运行结果为
aba aab baa