快速排序是一种非常高效的排序算法,它采用“分而治之”的思想,把大的拆分为小的,小的再拆分为更小的。其原理如下:对于一组给定的记录,通过一趟排序后,将原序列分为两部分,其中前一部分的所有记录均比后一部分的所有记录小,然后再依次对前后两部分的记录进行快速排序,递归该过程,直到序列中的所有记录均有序为止。
具体而言,算法步骤如下:
1)分解:将输入的序列array[m..n]划分成两个非空子序列array[m…k]和array[k+1…n],使array[m…k]中任一元素的值不大于array[k+1…n]中任一元素的值。
2)递归求解:通过递归调用快速排序算法分别对array[m…k]和array[k+1…n]进行排序。
3)合并:由于对分解出的两个子序列的排序是就地进行的,所以在array[m…k]和array[k+1…n]都排好序后不需要执行任何计算array[m…n]就已排好序。
以数组{38,65,97,76,13,27,49}为例。
第一趟排序过程如下:
初始化关键字[49 38 65 97 76 13 27 49]
第一次交换后:[27 38 65 97 76 13 49 49]
第二次交换后:[27 38 49 97 76 13 65 49]
j向左扫描,位置不变,第三次交换后:[27 38 13 97 76 49 65 49]
i向右扫描,位置不变,第四次交换后:[27 38 13 49 76 97 65 49]
j向左扫描[27 38 13 49 76 97 65 49]
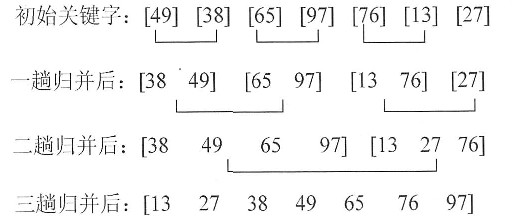
整个排序过程如下所示:
初始化关键字[49 38 65 97 76 13 27 49]
一趟排序之后:[27 38 13] 49 [76 97 65 49]
二趟排序之后:[13] 27 [38] 49 [49 65]76 [97]
三趟排序之后: 13 27 38 49 49 [65]76 97
最后的排序结果:13 27 38 49 49 65 76 97
程序示例如下:
public class Test
{
public static void sort(int[] array, int low, int high)
{
int i,j;
int index;
if(low>=high)
return;
i=low;
j=high;
index=array[i];
while(i<j)
{
while(i<j&&array[j]>=index)
j--;
if(i<j)
array[i++]=array[j];
while(i<j&&array[i]<index)
i++;
if(i<j)
array[j--]=array[i];
}
array[i]=index;
sort(array,low,i-1);
sort(array,i+1,high);
}
public static void quickSort(int[] array)
{
sort(array,0, array.Length-1);
}
public static void Main(String[] args)
{
int i=0;
int[] a={5,4,9,8,7,6,0,1,3,2};
int len=a.Length;
quickSort(a);
for(i=0;i<len; i++)
{
Console.Write(a[i]+"");
}
}
}
程序输出为:
0 1 2 3 4 5 6 7 8 9
当初始的序列整体或局部有序时,快速排序的性能将会下降,此时,快速排序将退化为冒泡排序。
快速排序的相关特点如下:
(1)最坏时间复杂度
最坏情况是指每次区间划分的结果都是基准关键字的左边(或右边)序列为空,而另一边的区间中的记录项仅比排序前少了一项,即选择的基准关键字是待排序的所有记录中最小或者最大的。例如,如果选取第一个记录为基准关键字,当初始序列按递增顺序排列时,每次选择的基准关键字都是所有记录中的最小者,这时记录与基准关键字的比较次数会增多。因此,在这种情况下,需要进行(n-1)次区间划分。对于第k(0<k<n)次区间划分,划分前的序列长度为(n-k+1),需要进行(n-k)次记录的比较。因此,当k从1到(n-1)时,进行的比较次数总共为n(n-1)/2,所以,在最坏情况下快速排序的时间复杂度为O(n
)。
(2)最好时间复杂度
最好情况是指每次区间划分的结果都是基准关键字左右两边的序列长度相等或者相差为1,即选择的基准关键字为待排序的记录中的中间值。此时,进行的比较次数总共为nlogn,所以,在最好情况下快速排序的时间复杂度为
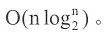
(3)平均时间复杂度
快速排序的平均时间复杂度为
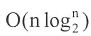
。虽然快速排序在最坏情况下的时间复杂度为O(n
2),但是在所有平均时间复杂度为
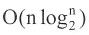
的算法中,快速排序的平均性能是最好的。
(4)空间复杂度
快速排序的过程中需要一个栈空间来实现递归。当每次对区间的划分都比较均匀时(即最好情况),递归树的最大深度为
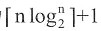
(logn为向上取整);当每次区间划分都使得有一边的序列长度为0时(即最好情况),递归树的最大深度为n。在每轮排序结束后比较基准关键字左右的记录个数,对记录多的一边先进行排序,此时,栈的最大深度可降为
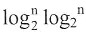
。因此,快速排序的平均空间复杂度为
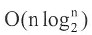
。
(5)基准关键字的选取
基准关键字的选择是决定快速排序算法性能的关键。常用的基准关键字的选择有以下方式:
1)三者取中。三者取中是指在当前序列中,将其首、尾和中间位置上的记录进行比较,选择三者的中值作为基准关键字,在划分开始前交换序列中的第一个记录与基准关键字的位置。
2)取随机数。取left(左边)和right(右边)之间的一个随机数m(left≤m≤right),用n[m]作为基准关键字。这种方法使得n[left]到n[right]之间的记录是随机分布的,采用此方法得到的快速排序一般称为随机的快速排序。
需要注意一个问题,就是快速排序与归并排序的区别与联系。快速排序与归并排序的原理都是基于分治思想,即首先把待排序的元素分成两组,然后分别对这两组排序,最后把两组结果合并起来。
而它们的不同点在于,进行的分组策略不同,后面的合并策略也不同。归并排序的分组策略是假设待排序的元素存放在数组中,那么其把数组前面一半元素作为一组,后面一半作为另外一组。而快速排序则是根据元素的值来分组,即大于某个值的元素放在一组,而小于的放在另外一组,该值称为基准。所以,对整个排序过程而言,基准值的挑选非常重要,如果选择不合适,太大或太小,那么所有的元素都分在一组了。总的来说,快速和归并排序,如果分组策略越简单,则后面的合并策略就越复杂,因为快速排序在分组时,已经根据元素大小来分组了,而合并的时候,只需把两个分组合并起来就行了,归并排序则需要对两个有序的数组根据大小合并。
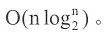
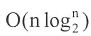 。虽然快速排序在最坏情况下的时间复杂度为O(n2),但是在所有平均时间复杂度为
。虽然快速排序在最坏情况下的时间复杂度为O(n2),但是在所有平均时间复杂度为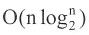 的算法中,快速排序的平均性能是最好的。
的算法中,快速排序的平均性能是最好的。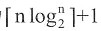 (logn为向上取整);当每次区间划分都使得有一边的序列长度为0时(即最好情况),递归树的最大深度为n。在每轮排序结束后比较基准关键字左右的记录个数,对记录多的一边先进行排序,此时,栈的最大深度可降为
(logn为向上取整);当每次区间划分都使得有一边的序列长度为0时(即最好情况),递归树的最大深度为n。在每轮排序结束后比较基准关键字左右的记录个数,对记录多的一边先进行排序,此时,栈的最大深度可降为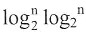 。因此,快速排序的平均空间复杂度为
。因此,快速排序的平均空间复杂度为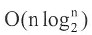 。
。