一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.3. 微分方程y"+2y'+y=shx的一个特解应具有形式(其中a,b为常数)______
- A.ashx
- B.achx
- C.ax2e-x+bex
- D.axe-x+bex
A B C D
C
[解析] 特征方程为r
2+2r+1=0,r=-1为二重特征根,而
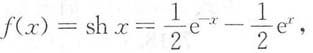
,故特解为y*=ax
2e
-x+be
x.
4. 下列命题中错误的是______
A.

B.

C.

不一定发散
D.
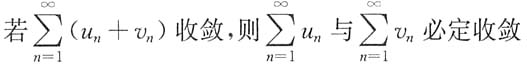
A B C D
D
[解析] 由级数收敛的性质知命题A正确.
由反证法可知命题B正确.
若设
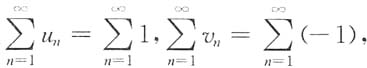
这两个级数都发散,但是
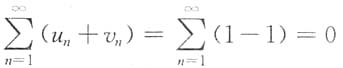
收敛,可知命题C正确,但命题D错误.
5. 设
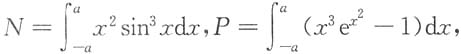
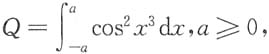
则______
- A.N≤P≤Q
- B.N≤Q≤P
- C.Q≤P≤N
- D.P≤N≤Q
A B C D
D
[解析] x
2sin
3x是奇函数,故N=0,x
3e
x2是奇函数,故
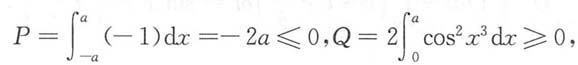
所以P≤N≤Q.
7. 设函数
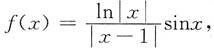
则f(x)______
- A.有1个可去间断点,1个跳跃间断点.
- B.有1个跳跃间断点,1个无穷间断点.
- C.有2个无穷间断点.
- D.有2个跳跃间断点.
A B C D
A
[解析]
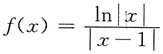
在x=0,x=1无定义,而
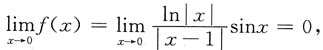
所以x=0为可去间断点.
又
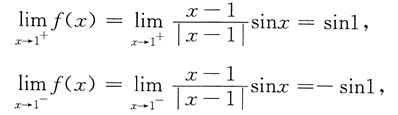
所以x=1为跳跃间断点.
9. 设A为n阶实矩阵,A
T为A的转置矩阵,对于线性方程组(Ⅰ):Ax=0和(Ⅱ):A
TAx=0,必有______
- A.(Ⅱ)的解是(Ⅰ)的解,(Ⅰ)的解也是(Ⅱ)的解.
- B.(Ⅱ)的解是(Ⅰ)的解,但(Ⅰ)的解不是(Ⅱ)的解.
- C.(Ⅰ)的解不是(Ⅱ)的解,(Ⅱ)的解也不是(Ⅰ)的解.
- D.(Ⅰ)的解是(Ⅱ)的解,但(Ⅱ)的解不是(Ⅰ)的解.
A B C D
A
[解析] 若Ax=0,则显然有A
TAx=0,即(Ⅰ)的解是(Ⅱ)的解;反过来,若A
TAx=0则有
x
TA
TAx=(Ax)
T(Ax)=0,
从而推出Ax=0.
因为若设Ax=(a
1,a
2,…,a
n)
T,则
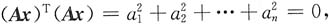
于是有
a
1=a
2=…=a
n=0,
即Ax=0.说明(Ⅱ)的解也是(Ⅰ)的解.
二、填空题1. 设总体X~P(λ),X
1,X
2,…,X
n是来自X的简单随机样本,它的均值和方差分别为
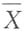
和S
2,则
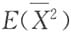
和E(S
2)分别为______.
[解析]
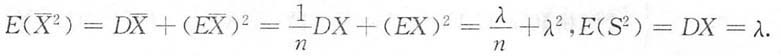
2. 设X
1,X
2,…,X
n为来自总体N(0,σ
2)的样本,且随机变量

则常数C=______.
3. 幂级数
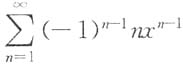
在收敛域(-1,1)内的和函数S(x)为______.
4. 设X,Y为随机变量,已知D(X)=25,D(Y)=36,X与Y的相关系数ρ
XY=0.4,则cov(2X-3Y,X-Y)=______.
98
[解析] 因为
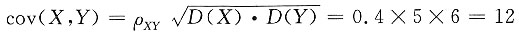
,则
cov(2X-3Y,X-Y)=2cov(X,X)-2coy(X,Y)-3cov(X,Y)+3cov(Y,Y)
=2D(X)+3D(Y)-5coy(X,Y)
=2×25+3×36-5×12=98.
5. 设α
1=[1,0,-1,2]
T,α
2=[2,-1,-2,6]
2,α
3=[3,1,t,4]
2,β=[4,-1,-5,10]
2,已知β不能由α
1,α
2,α
3线性表出,则t=______.
-3
[解析]

6. 设y(x)是微分方程y"+(x+1)y'+x
2y=x的满足y(0)=0,y'(0)=1的解,并设
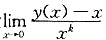
存在且不为零,则正整数k=______,该极限值=______.
[解析] 由y(0)=0知,所求极限为“
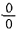
”型,又

由初始条件y'(0)=1,若k=1,则上述极限为0,不符,故k≥2.

由所给方程知,y"(0)=[x-(x+1)y'-x
2y]|
x=0=-1.所以当k=2时,上述极限为
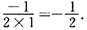
于是知
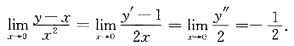
故k=2,
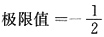
.
三、解答题共70分.解答应写出文字说明、证明过程或演算步骤.1. 设f(x)连续,
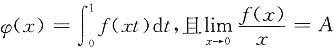
.求φ'(x),并讨论φ'(x)在x=0处的连续性.
解:当x≠0时,
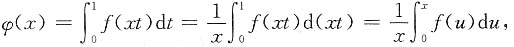
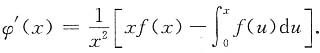
当x=0时,
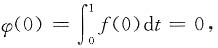
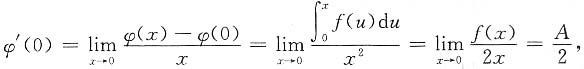
则
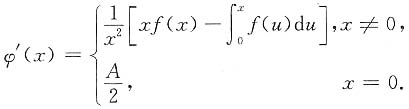
因为
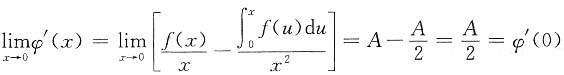
,所以φ'(x)在x=0处连续.
2. 设向量组α
1=[a
11,a
21,…,a
n1]
T,α
2=[a
12,a
22,…,a
n2]
T,…,α
s=[a
1s,a
2s,…,a
ns]
T.证明:向量组α
1,α
2,…,α
s线性相关(线性无关)的充要条件是齐次线性方程组
有非零解(有唯一零解).
证:
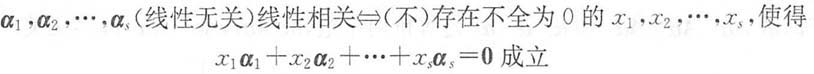

有非零解(唯一零解).
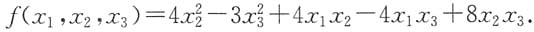
3. 写出二次型f的矩阵表达式;
解:二次型的矩阵

则二次型f的矩阵表达式f=x
TAx.
4. 用正交变换把二次型f化为标准形,并写出相应的正交矩阵.
解:A的特征多项式|A-λE|=-(6+λ)(1-λ)(6-λ),则A的特征值λ
1=-6,λ
2=1,λ
3=6.
λ
1=-6对应的正交单位化特征向量
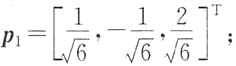
λ
2=1对应的正交单位化特征向量
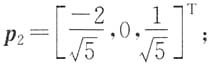
λ
3=6对应的正交单位化特征向量
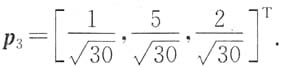
令正交矩阵
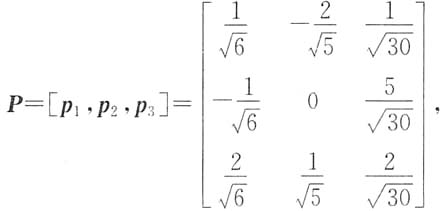
所求正交变换
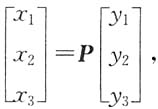
二次型f的标准型
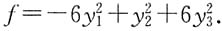
5.
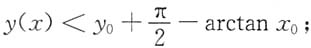
证:将微分方程(x
2+y
2)dy=dx-dy变形为
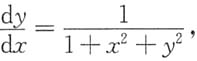
于是
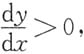
则y=y(x)为严格单调增函数,根据单调有界准则,只要证明y(x)有界即可.
对
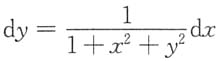
两边从x
0到x积分,得
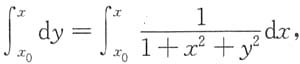
于是
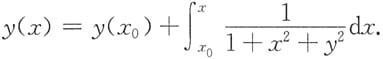
设x≥x
0,则
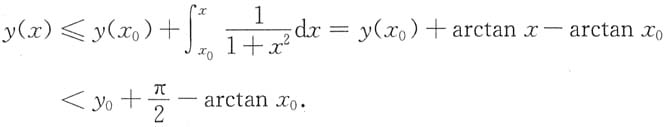
6.
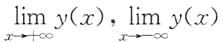
均存在.
证:y(x)有上界,所以
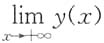
存在.
同理可证,当x≤x
0时,y(x)有下界,所以
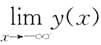
也存在.
故
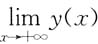
存在,
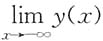
也存在.
[解析] 本题以微分方程的概念为载体,考查一元微积分学的综合知识,是一道有一定难度的综合题.
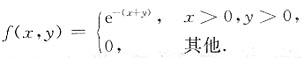
7. 求Z=Y-X的密度函数;
解:解法一 分布函数法.
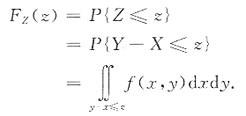
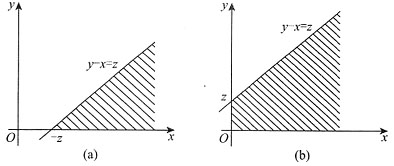
①当z≤0时,f(z,y)的非零区域与{y-x≤z}的交集为下图(a)中的阴影部分,
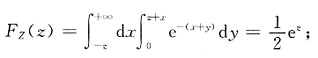
②当x>0时,f(x,y)的非零区域与{y-x≤z}的交集为下图b中的阴影部分.
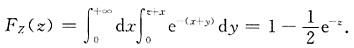
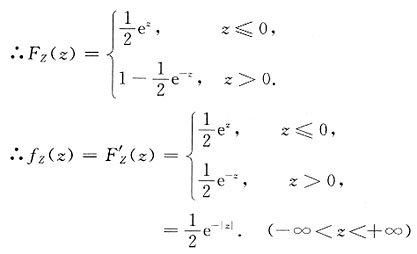
解法二 密度函数法(如下图).
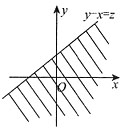
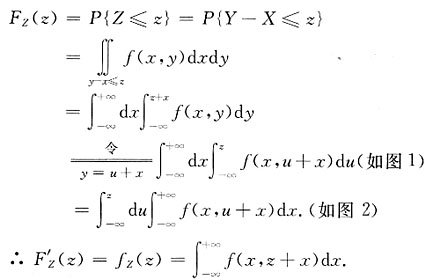
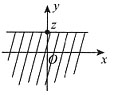
图1
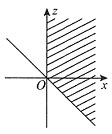
图2
与X,Y的联合密度函数配套:
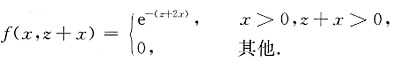
ⅰ)当z≤0时,

ⅱ)当z>0时,
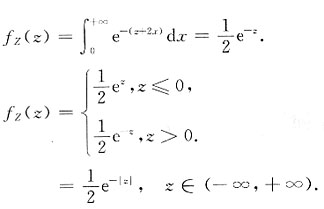
8. 求数学期望E(X+Y).
解:
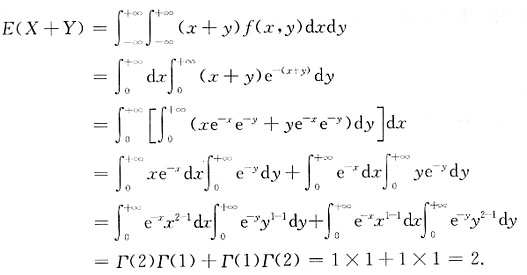
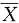 (i=1,2,…,n).求:
(i=1,2,…,n).求:9. D(Y
i);
解:由
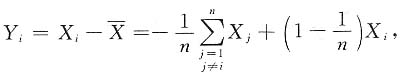
得
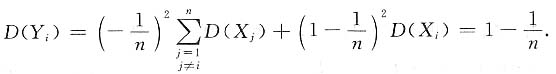
10. Cov(Y
1,Y
n).
解:因为X
1,X
2,…,X
n(n>2)相互独立,
所以
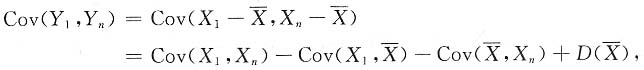
由
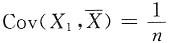
得

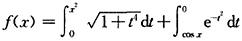 在区间(-∞,+∞)内零点个数为______
在区间(-∞,+∞)内零点个数为______ ,从而知在区间
,从而知在区间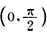 内f(x)至少有1个零点,又当x>0时,
内f(x)至少有1个零点,又当x>0时,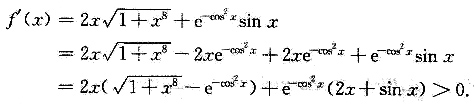
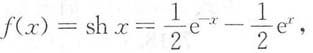 ,故特解为y*=ax2e-x+bex.
,故特解为y*=ax2e-x+bex.

 不一定发散
不一定发散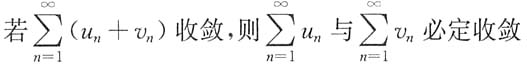
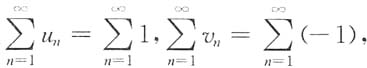 这两个级数都发散,但是
这两个级数都发散,但是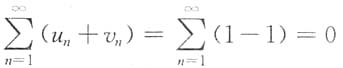 收敛,可知命题C正确,但命题D错误.
收敛,可知命题C正确,但命题D错误.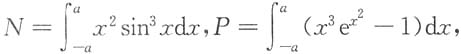
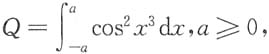 则______
则______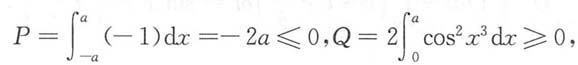
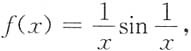 当x→0时为无界变量,不是无穷大.令g(x)=x,当x→0时为无穷小,可排除A.设x→0时,令f(x)=x2,
当x→0时为无界变量,不是无穷大.令g(x)=x,当x→0时为无穷小,可排除A.设x→0时,令f(x)=x2,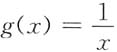 可排除B,C.
可排除B,C.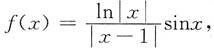 则f(x)______
则f(x)______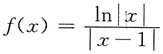 在x=0,x=1无定义,而
在x=0,x=1无定义,而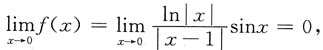
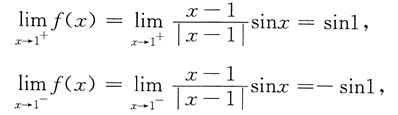
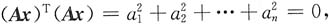 于是有
于是有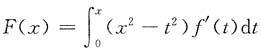 的导数与x2为等价无穷小,则f'(0)等于______
的导数与x2为等价无穷小,则f'(0)等于______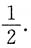
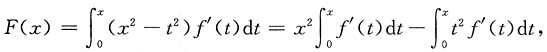
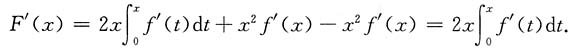
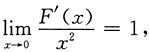 即
即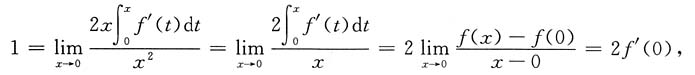
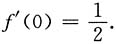
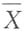 和S2,则
和S2,则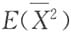 和E(S2)分别为______.
和E(S2)分别为______.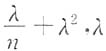
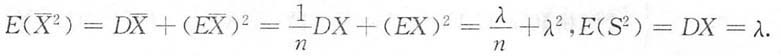
 则常数C=______.
则常数C=______.
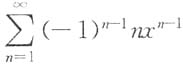 在收敛域(-1,1)内的和函数S(x)为______.
在收敛域(-1,1)内的和函数S(x)为______.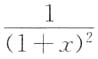
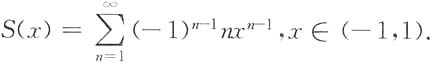
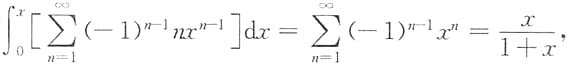 即
即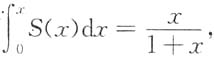 故
故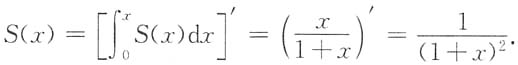
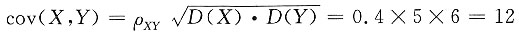 ,则
,则
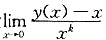 存在且不为零,则正整数k=______,该极限值=______.
存在且不为零,则正整数k=______,该极限值=______.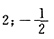
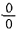 ”型,又
”型,又

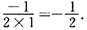
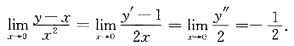
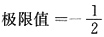 .
.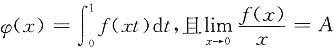 .求φ'(x),并讨论φ'(x)在x=0处的连续性.
.求φ'(x),并讨论φ'(x)在x=0处的连续性.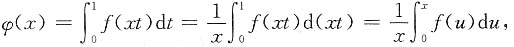
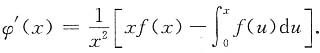
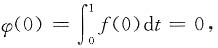
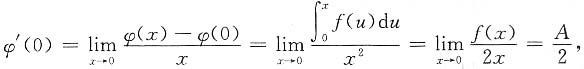
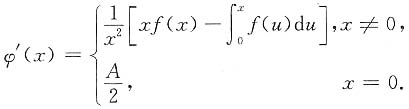
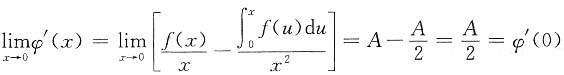 ,所以φ'(x)在x=0处连续.
,所以φ'(x)在x=0处连续.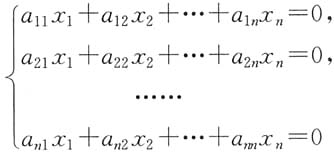
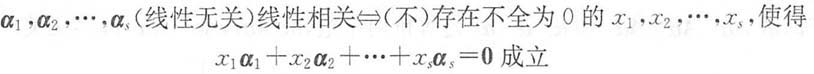

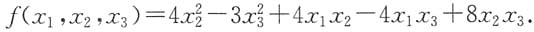
 则二次型f的矩阵表达式f=xTAx.
则二次型f的矩阵表达式f=xTAx.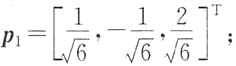
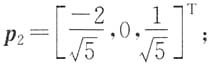
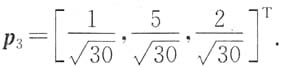
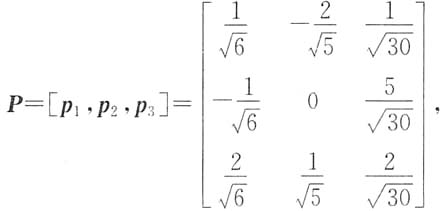
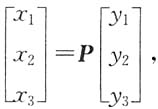 二次型f的标准型
二次型f的标准型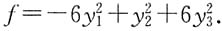
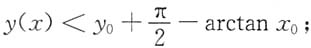
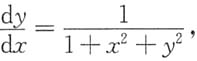 于是
于是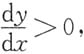 则y=y(x)为严格单调增函数,根据单调有界准则,只要证明y(x)有界即可.
则y=y(x)为严格单调增函数,根据单调有界准则,只要证明y(x)有界即可.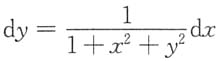 两边从x0到x积分,得
两边从x0到x积分,得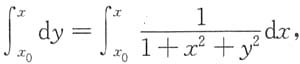 于是
于是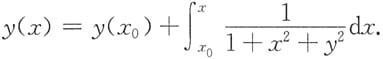
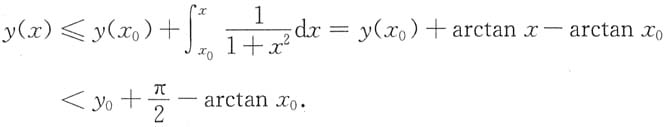
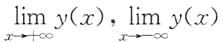 均存在.
均存在.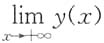 存在.
存在.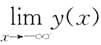 也存在.
也存在.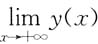 存在,
存在,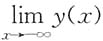 也存在.
也存在.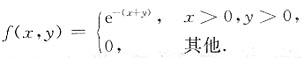
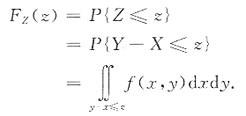
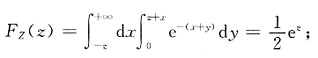
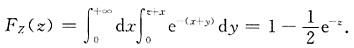

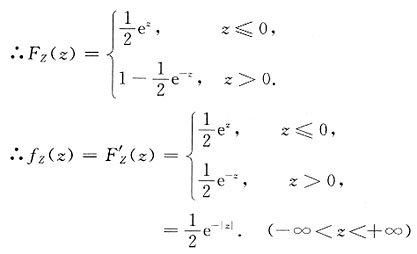

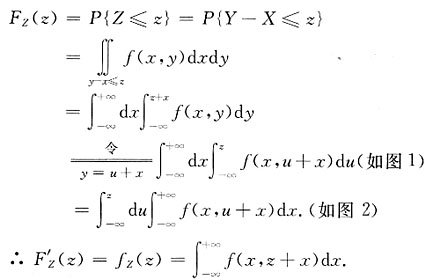


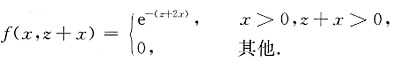

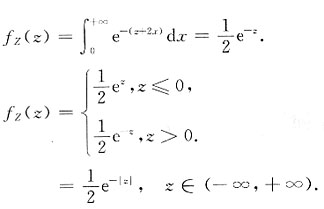
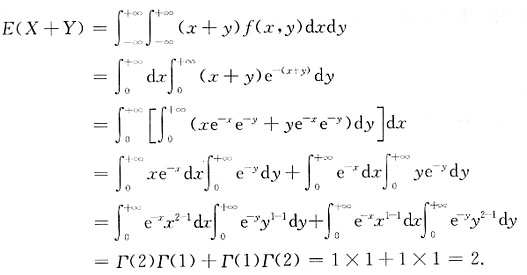
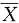 (i=1,2,…,n).求:
(i=1,2,…,n).求: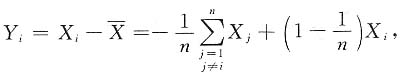
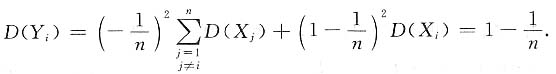
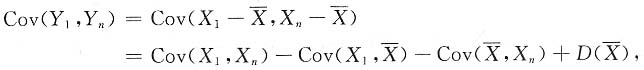
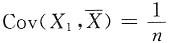 得
得
