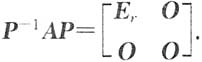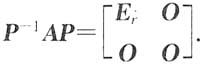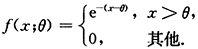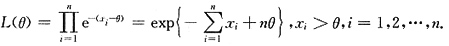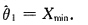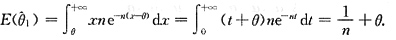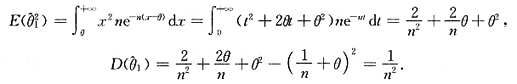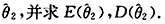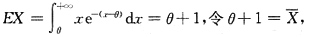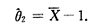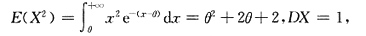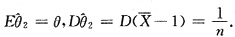一、选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的.1. 考虑一元函数f(x)的下列4条性质:
①f(x)在[a,b]上连续;
②f(x)在[a,b]上可积;
③f(x)在[a,b] 上可导;
④f(x)在[a,b]上存在原函数,
以
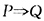
表示由性质P可推出性质Q,则有______
A.
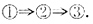
B.

C.
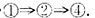
D.
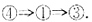
A B C D
B
[解析] 因可导必连续,连续函数必存在原函数,故B正确.
A不正确,虽然由①(连续)可推出②(可积),但由②(可积)推不出③(可导).例如f(x)=|x|在[-1,1]上可积:
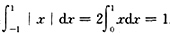
.但f(x)=|x|在x=0处不可导.
C不正确.由②(可积)推不出④(存在原函数),例如
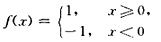
在[-1,1]上可积,则
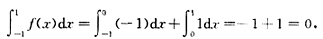
但f(x)在[-1,1]上不存在原函数.因为如果存在原函数F(x),那么只能是F(x)=|x|+C的形式,而此函数在点x=0处不可导,在区间[-1,1]上它没有做原函数的“资格”.
D不正确.因为由④(存在原函数)推不出①(函数连续).例如:
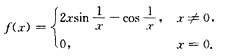
它存在原函数
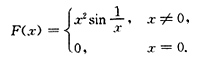
但f(x)并不连续.即存在原函数的函数f(x)可以不连续.
2. 设X
1,X
2,…,X
8是来自总体N(2,1)的简单随机样本,则统计量
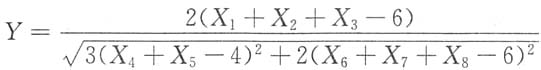
服从______
- A.χ2(2)
- B.χ2(3)
- C.t(2)
- D.t(3)
A B C D
C
[解析]
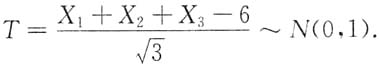
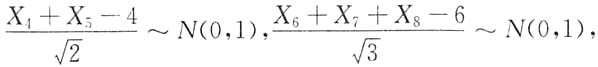
且它们相互独立,所以
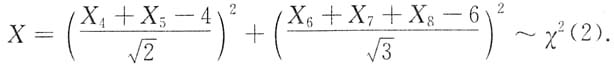
所以由T与X相互独立得,
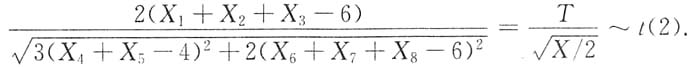
因此本题选C.
4. 已知随机变量(X,Y)在区域D={(x,y)|-1<x<1,-1<y<1}上服从均匀分布,则______
A.P{X+Y≥0}=
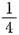
.
B.P{X-Y≥0}=
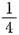
.
C.P{max(X,Y)≥0}=
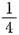
.
D.P{min(X,Y)≥0}=
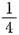
.
A B C D
D
[解析] 显然这是一道计算性选择题,需要通过计算才能确定正确选项.由题设知(X,Y)的概率密度函数
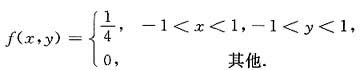
选项C、D易于计算,且P{min(X,Y)≥0}=P{X≥0,Y≥0}=
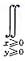
f(x,y)dxdy=
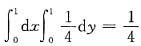
,选择D.
又P{max(X,Y)≥0}=1-P{max(X,Y)<0}=1-P{X<0,Y<0}

P{X+Y≥0}=
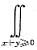
f(x,y)dxdy
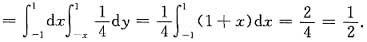
P{X-Y≥0)=
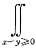
f(x,y)dxdy
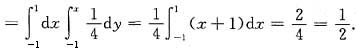
所以选项A、B、C都不正确.
如果将已知条件改为:(X,Y)的概率分布为

,那么正确选项是什么?
由题设不难计算出:
P{mix(X,Y)≥0}=P{X≥0,Y≥0}=P{X=1,Y=1}+P{X=1,Y=2}=
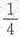
.
P{max(X,Y)≥0}=1-P{max(X,Y)<0}=1-P{X<0,Y<0}=1.
P{X+Y≥0}=P{X=-1,Y=1}+P{X=-1,Y=2}+P{X=1,Y=1}+P{X=1,Y=2}=1.
P{X-y≥0}=P{X≥Y}=P{X=1,Y=1}=0.
选项D正确,其他选项均不正确.
5. 极限
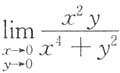
______
A.等于0
B.不存在
C.等于
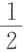
D.存在且不等于0及
A B C D
B
[解析] 取y=x,则
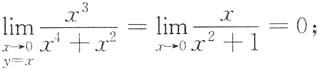
取y=x
2,则
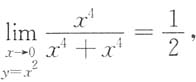
故原极限不存在.
6. 设随机变量X服从正态分布N(1,σ
2),其分布函数为F(x),则对任意实数x,有______。
- A.F(x)+F(-x)=1
- B.F(1+x)+F(1-x)=1
- C.F(x+1)+F(x-1)=1
- D.F(1-x)+F(x-1)=1
A B C D
B
[考点] 考查随机变量的分布函数
[解析] 由于X~N(1,σ
2),所以
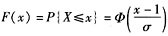
。
由此可知相应的四个选项是
A.
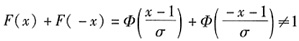
;
B.
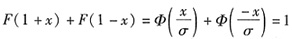
;
C.
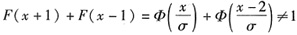
;
D.
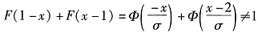
。因为
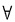
x∈R它们都要成立,因此选B。
7. 设A,B,C是两两独立且不能同时发生的随机事件,且P(A)=P(B)=P(C)=x,则x的最大值为______
A.
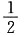
B.1
C.
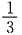
D.
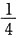
A B C D
A
[解析] 由题设P(AB)=P(AC)=P(BC)=x
2,P(ABC)=0,于是
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)=3x-3x
2,
而P(A+B+C)≥P(A+B)=P(A)+P(B)-P(AB)=2x-x
2,故有
3x-3x
2≥2x-x
2,解得

,故选A.
8. 设二维随机变量(X,Y)的概率密度
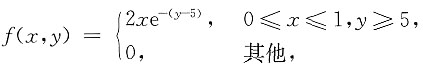
则E(XY)=______
A B C D
D
[解析] 由题意,知f(x,y)=f
X(x)f
Y(y),其中
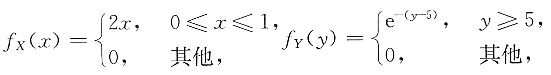
所以,X与Y相互独立.由于
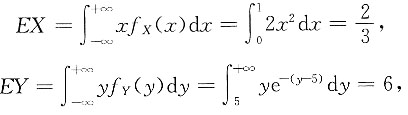
则
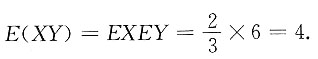
选D.
9. 设α
1,α
2,α
3是齐次方程组Ax=0的基础解系,那么Ax=0的基础解系还可以是______
- A.a1+a2,a2+a3,α3-α1.
- B.α1+α2,α2+α3,α1+2α2+α3.
- C.α1+2α2,2α2+3α3,3α3+α1.
- D.α1+α2+α3,2α1-3α2+22α3,3α1+5α2-5α3.
A B C D
C
[解析]

而

C中的三个向量线性无关,是Ax=0的一个基础解系.
选C.
二、填空题1. 设X~N(0,2
2),X
k(k=1,2,3,4)是来自总体X的简单样本,令S
2=a(X
1-2X
2)
2+b(3X
3-4X
4)
2, 若统计量S
2服从χ
2(n)分布,则a,b,n分别等于______.
[解析] 设Y
1=X
1-2X
2,Y
2=3X
3-4X
4,由E(X
i)=0,D(X
i)=σ
2=4,i=1,2,3,4.则
E(Y
1)=E(Y
2)=0,D(Y
1)=D(X
1-2X
2)=D(X
1)+4D(X
2)=20,
D(Y
2)=D(3X
3-4X
4)=9D(X
3)+16D(X
4)=100.
因此Y
1~N(0,20),Y
2~N(0,100).规范化得
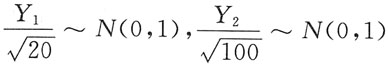
,
由χ
2分布的定义知

故
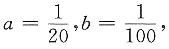
自由度为2.
2. 设级数
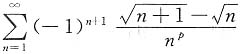
条件收敛,则p的取值范围是______.
3. 设X
1,X
2,X
3,X
4是来自正态总体X~N(μ,σ
2)的样本,则统计量
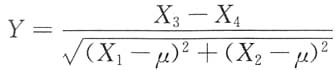
服从的分布是______.
t(2)
[解析] 因为X~N(μ,σ
2),所以X
3-X
4~N(0,2σ
2),

又
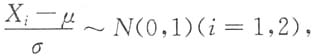
故

所以
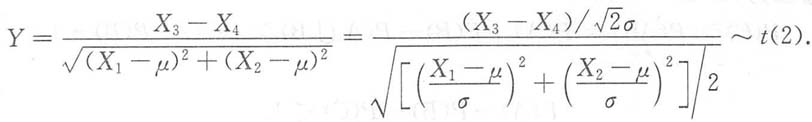
4. 设f(x)有二阶连续导数且z=f(e
xsiny)满足
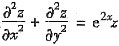
,则函数f(x)=______
c1ex+c2e-x(c1,c2为任意常数)
[考点] 复合函数求偏导数及解二阶常系数齐次微分方程.
[解析]
,代入
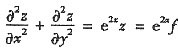
,得f"=f,即f"-f=0.
特征方程为λ
2-1=0,λ
1=1,λ
2=-1,从而
f(x)=c1ex+c2e-x (c1,c2为任意常数).
5.
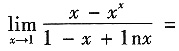
______.
2
[解析] 运用洛必达法则,
原式
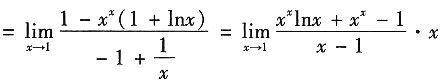
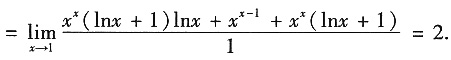
6. 设A,B均为四阶方阵,r(A)=3,r(B)=4,其伴随矩阵分别为A
*,B
*,则r(A
*B
*)=______.
1
[解析] 分别求出r(A*),r(B*).如果r(B*)为满秩矩阵,则r(A*B*)=r(A*).
因r(A)=3,故r(A*)=1(因当r(A)=n-1时,r(A*)=1).又r(B)=4,故r(B*)=4(因r(B)=n,则r(B*)=72),即B*为满秩矩阵,于是
r(A*B*)=r(A*)=1.
三、解答题共70分.解答应写出文字说明、证明过程或演算步骤.1. 设A是n阶矩阵,A的第i行第j列元素为a
ij=i·j,i=1,2,…,n,j=1,2,…,n,B是n阶矩阵,B的第i行第j列元素为b
ij=i
2,i=1,2,…,n,j=1,2,…,n.证明A~B.
证:由题意,
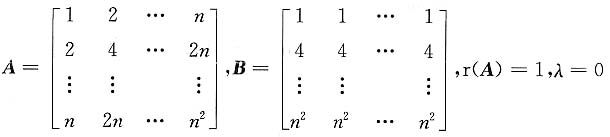
是A的n-1重特征值,A的非零特征值
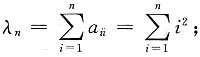
r(B)=1,μ=0是B的n-1重特征值,B的非零特征值
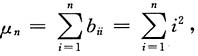
A是实对称阵,故
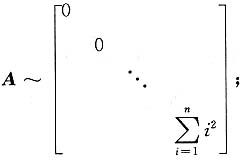
B对应于n-1重特征值μ=0,因r(B)=1,故有n-1个线性无关的特征向量,故B~

故
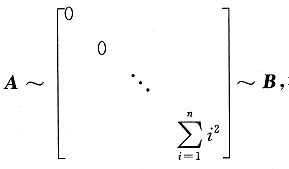
得证A~B.
2. 设向量组(Ⅰ)与向量组(Ⅱ),若(Ⅰ)可由(Ⅱ)线性表示,且r(Ⅰ)=r(Ⅱ)=r.证明:(Ⅰ)与(Ⅱ)等价.
证:设(Ⅰ)的一个极大无关组为ξ1,ξ2,…,ξr,(Ⅱ)的一个极大无关组为η1,η2,…,ηr.
因为(Ⅰ)可由(Ⅱ)表示,即ξ1,ξ2,…,ξr可由η1,η2,…,ηr线性表示,于是
r(ξ1,ξ2,…,ξr,η1,η2,…,ηr)=r(η1,η2,…,ηr)=r.
又ξ1,ξ2,…,ξr线性无关,则ξ1,ξ2,…,ξr也可作为ξ1,ξ2,…,ξr,η1,η2,…,ηr的一个极大无关组,于是η1,η2,…,ηr也可由ξ1,ξ2,…,ξr表示,即(Ⅱ)也可由(Ⅰ)表示,得证.
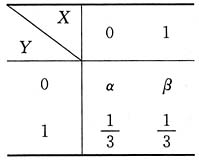
3. 证明X与Y不相关的充分必要条件是事件{Y=1}与{X+Y=1}相互独立;
解:由概率分布的性质知
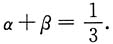
X与Y不相关
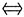
cov(X,Y)=E(XY)-EX·EY=0.
X的概率分布为
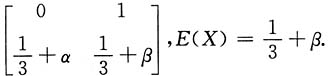
Y的概率分布为
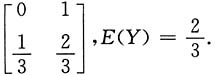
XY的概率分布为
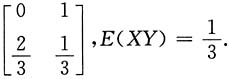
则

故X与Y不相关
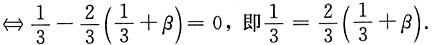
另一方面,事件{Y=1}与{X+Y=1}相互独立的充分必要条件是
P{Y=1,X+Y=1}=P{Y=1}·P{X+Y=1}.
而今已知
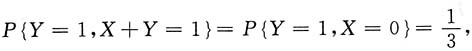
且
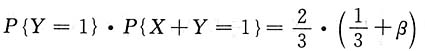
故事件{Y=1}与{X+Y=1}相互独立的充分必要条件也是
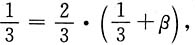
所以X与Y不相关的充分必要条件是事件{Y=1}与{X+Y=1}相互独立.
4. 若X与Y不相关,求X与Y的边缘分布.
解:若X与Y不相关,则
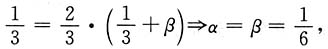
故X的概率分布为
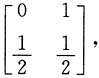
Y的概率分布为
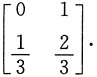
5. 若正项级数
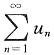
收敛,证明:
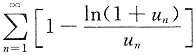
收敛.
证:因为
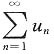
收敛,所以
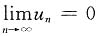
,
当x>0时,ln(1+x)<x,于是
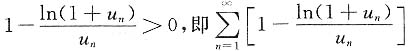
为正项级数,
而
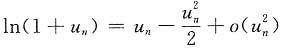
,
所以
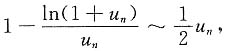
再由

收敛,故

收敛.
6. 设A是n阶矩阵,满足A
2=A,且r(A)=r(0<r≤n).证明:
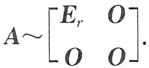
其中E
r是r阶单位阵.
证:方法一 A
2=A,A的特征值取值为1,0,由A-A
2=A(E-A)=O知
r(A)+r(E-A)≤n,
r(A)+r(E-A)≥r(A+E-A)=r(E)=n,
故r(A)+r(E-A)=n,r(A)=r,从而r(E-A)=n-r.
对λ=1,(E-A)X=0,因r(E-A)=n-r,故有r个线性无关特征向量,设为ξ
1,ξ
2,…,ξ
r;
对λ=0,(0E-A)X=0,即AX=0,因r(A)=r,有n-r个线性无关特征向量,设为ξ
r+1,ξ
r+2,…,ξ
n.
故存在可逆阵
P=[ξ
1,ξ
2,…,ξ
n],
使得
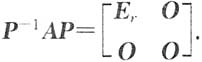
方法二 r(A)=r,A有r个列向量线性无关,设为前r列,将A按列分块,有
A
2=A[ξ
1,ξ
2,…,ξ
n]=[ξ
1,ξ
2,…,ξ
n]=A,
即Aξ
i=ξ
i,i=1,2,…r,故λ=1至少是r重根,又r(A)=r,AX=0有n-r个线性无关解,设为η
r+1,η
r+2,…,η
n,即Aη
j=0,j=r+1,…,n.故λ=0是A的特征值,η
j,j=r+1,…,n是对应的特征向量.
令P=[ξ
1,ξ
2,…,ξ
r,η
r+1,…,η
n],有
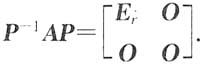
7. 求θ的最大似然估计量
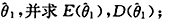
解:似然函数为:
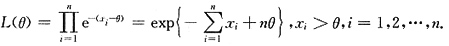
显然L(θ)是θ的单调增函数,因此θ的最大似然估计量为
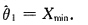
又X
min的概率密度为g(x)=ne
-n(x-ξ),x>θ,故
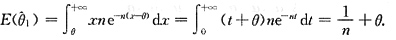
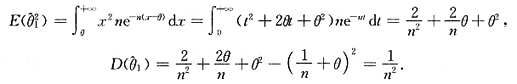
8. 求θ的矩估计量
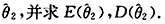
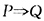 表示由性质P可推出性质Q,则有______
表示由性质P可推出性质Q,则有______

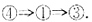
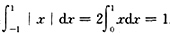 .但f(x)=|x|在x=0处不可导.
.但f(x)=|x|在x=0处不可导.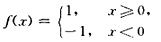
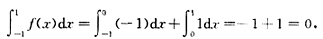
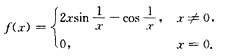
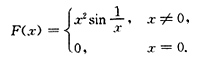
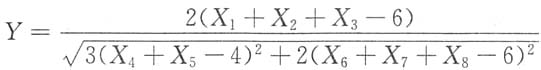 服从______
服从______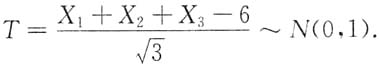
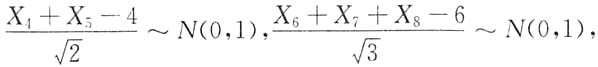 且它们相互独立,所以
且它们相互独立,所以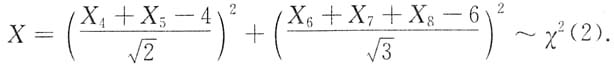
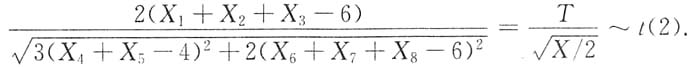
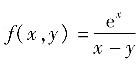 ,则______.
,则______.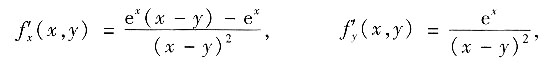
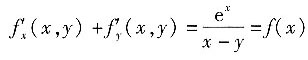 ,故此题选D.
,故此题选D.
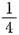 .
.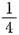 .
.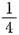 .
.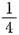 .
.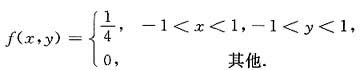
 f(x,y)dxdy=
f(x,y)dxdy=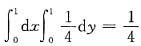 ,选择D.
,选择D.
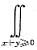 f(x,y)dxdy
f(x,y)dxdy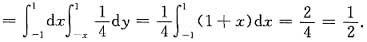
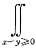 f(x,y)dxdy
f(x,y)dxdy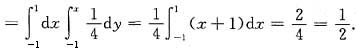
 ,那么正确选项是什么?
,那么正确选项是什么?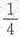 .
. ______
______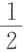
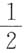
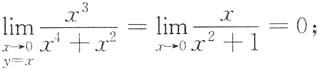 取y=x2,则
取y=x2,则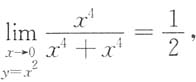 故原极限不存在.
故原极限不存在.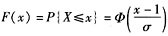 。
。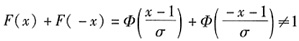 ;
;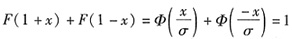 ;
;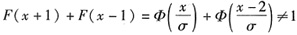 ;
;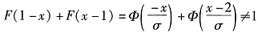 。因为
。因为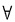 x∈R它们都要成立,因此选B。
x∈R它们都要成立,因此选B。
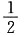
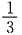
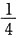
 ,故选A.
,故选A.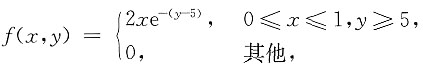 则E(XY)=______
则E(XY)=______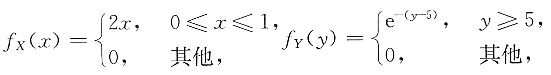
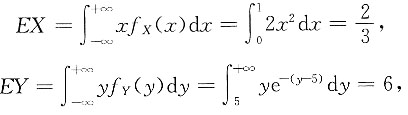
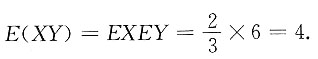


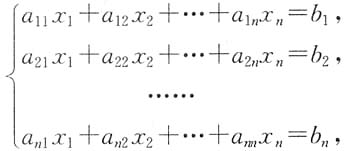 则有______
则有______ |A|=0(反证,若|A|≠0,用克拉默法则,方程组必有解);B项方程组有解,|A|可能为零,也可能不为零;C项|A|=0,方程组也可能有解;D项
|A|=0(反证,若|A|≠0,用克拉默法则,方程组必有解);B项方程组有解,|A|可能为零,也可能不为零;C项|A|=0,方程组也可能有解;D项 ,反过来,若方程组有唯一解
,反过来,若方程组有唯一解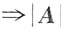 一定不为零.
一定不为零.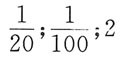
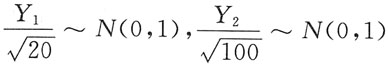 ,
,
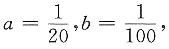 自由度为2.
自由度为2.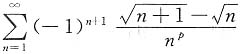 条件收敛,则p的取值范围是______.
条件收敛,则p的取值范围是______.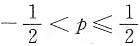
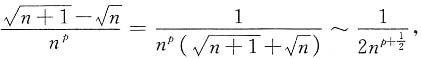
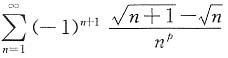 条件收敛,所以
条件收敛,所以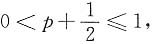 即p的范围是
即p的范围是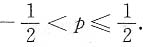
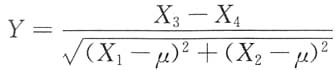 服从的分布是______.
服从的分布是______. 又
又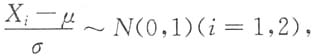
 所以
所以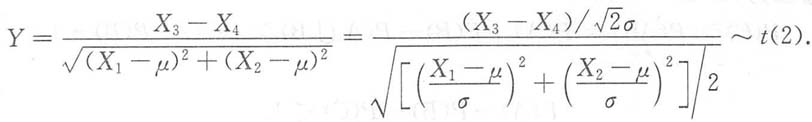
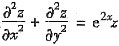 ,则函数f(x)=______
,则函数f(x)=______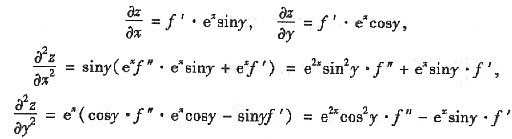
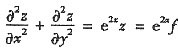 ,得f"=f,即f"-f=0.
,得f"=f,即f"-f=0.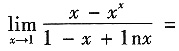 ______.
______.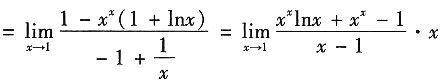
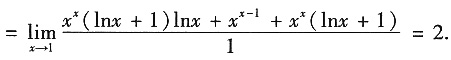
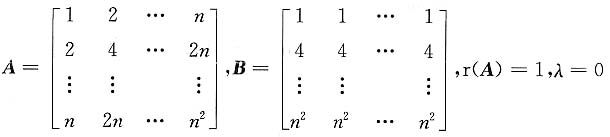
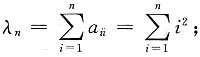 r(B)=1,μ=0是B的n-1重特征值,B的非零特征值
r(B)=1,μ=0是B的n-1重特征值,B的非零特征值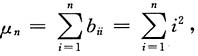 A是实对称阵,故
A是实对称阵,故
 故
故 得证A~B.
得证A~B.
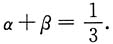
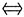 cov(X,Y)=E(XY)-EX·EY=0.
cov(X,Y)=E(XY)-EX·EY=0.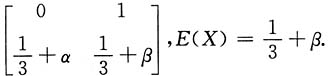
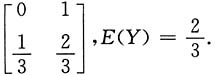

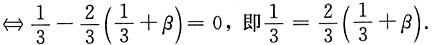
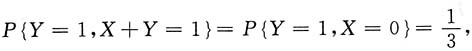 且
且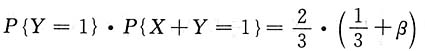
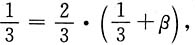 所以X与Y不相关的充分必要条件是事件{Y=1}与{X+Y=1}相互独立.
所以X与Y不相关的充分必要条件是事件{Y=1}与{X+Y=1}相互独立.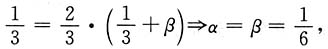
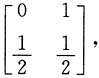 Y的概率分布为
Y的概率分布为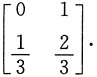
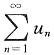 收敛,证明:
收敛,证明: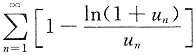 收敛.
收敛.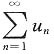 收敛,所以
收敛,所以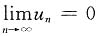 ,
,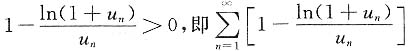 为正项级数,
为正项级数,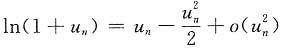 ,
,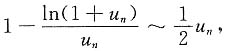 再由
再由 收敛,故
收敛,故 收敛.
收敛.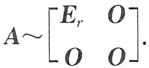 其中Er是r阶单位阵.
其中Er是r阶单位阵.