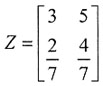计算题1. 如图所示电路为正弦稳态电路，已知电阻消耗的功率P=15W，电源电压
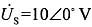
，电压有效值U
L=10V，且电感电压超前电源电压90°。求电阻R、感抗X
L和容抗X
C。
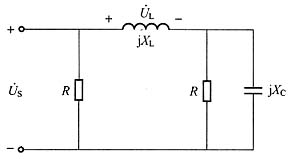
解：求解电路如图1所示，利用相量法求解。
由电阻特性可得：
根据电感电压超前电源电压90°可得：
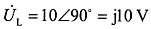
则有：
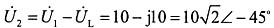
电阻消耗的功率P=15W，可得：
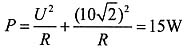
，R=20Ω
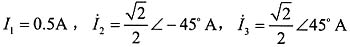
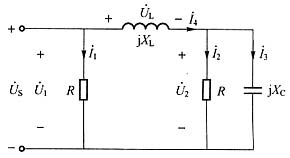
图1
可得：
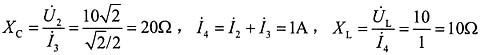
电路如图2所示。
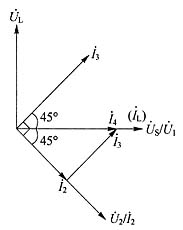
图2
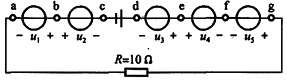
2. 下图所示电源电压为：U
0=60V，
，
，
，
，
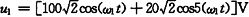
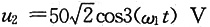
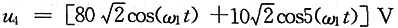
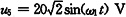
。试求：U
ab、U
ac、U
ad、U
ae、U
af。
3. 在下图所示电路中开关SW闭合前电路已处于稳态，在t=0时刻SW闭合，试用时域分析法求t≥0时的响应u(t)，并指出其中的零输入响应分量和零状态响应分量。
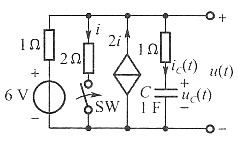
解：(1)计算初值SW闭合前，即t=0
-时，由题中电路图得：i(0
-)=0，u
C(0
-)=6V；
换路定理：u
C(0
+)=u
C(0
-)=6V；
t=0
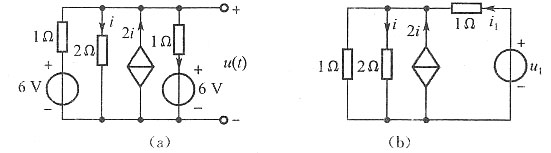
+时，电路如下图(a)所示，有u(0
+)(1+1+0.5)=2i(0
+)+6+6，u(0
+)=2i(0
+)得u(0
+)=8V
(2)计算终值t=∞时电路如题图所示：i
C(∞)=0，u(∞)=2i(∞)
u(∞)=6-[i(∞)-2i(∞)]得u(∞)=12V
(3)求时间常数，从电容两端看进去，当电源短路时，等效电路如下图(b)所示，有受控源可在端口加电压u
1(t)，求出相应电流i
1(t)，得u
1=3i
1，则等效电阻为3Ω，
τ=RC=3s
(4)代入三要素法公式，求得全响应为
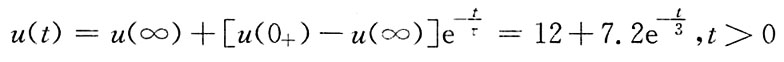
零输入响应分量为
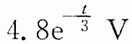
，t＞0
零状态响应分量为
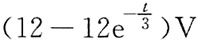
，t＞0
4. 已知电路图1(a)中电压表读数为：V
1为30V；V
2为60V；电路图1(b)：V
1为15V，V
2为80V，V
3为100V(电压表的读数为正弦电压的有效值)。求图中电源电压u
S的有效值U
S。
解：(1)把图1(a)转化为相量模型图，如图2(a)所示。设I=I∠0°为参考相量，则
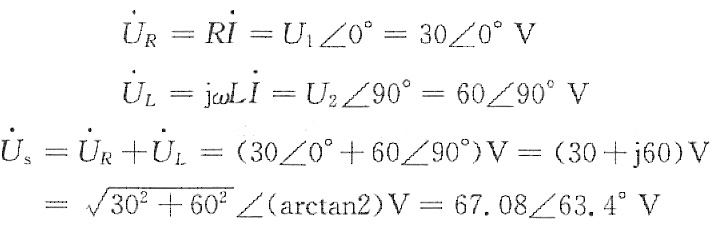
所以电源电压有效值U
S=67.08V。
(2)把图1(b)转化为相量模型图，如图2(b)所示。设
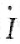
=I∠0°为参考相量，则
所以电源电压有效值U
S=25V
5. 电路如图所示，列写下图所示电路的状态方程。
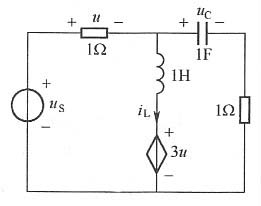
解：根据分流原理并结合题图所示电路，对电容建立电流方程可得：
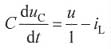
根据分压原理，对电感建立电压方程可得：
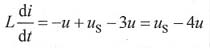
补充方程为：
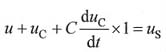
消元，代入数据，经整理后可得电路的状态方程如下：
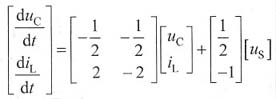
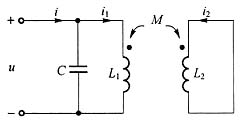
6. 如图所示一端口电路中，L
1=8H，L
2=2H，M=2H，C=6μF。求电路的谐振角频率。
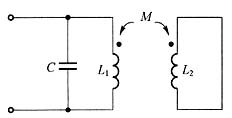
解：利用相量法求解电路，求解电路如图所示。
对于右侧电路运用KVL可得：
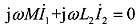
代入已知量得：
将互感等效到左侧电路，得：
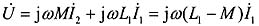
则从变压器的原边看进去，电路的等效电感为：L
eq=L
1-M=6H
电路的谐振角频率为：
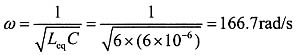
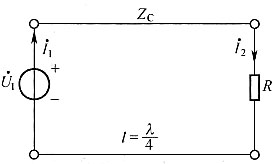
7. 电路如下图所示，1/4波长的无损耗均匀传输线，特性阻抗Z
C=250Ω，终端接R=100Ω的负载，始端接电压源
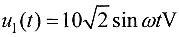
，求终端电流
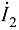
与始端电流
。
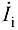
8. 如下图所示，用结点电压法求电压U
3。
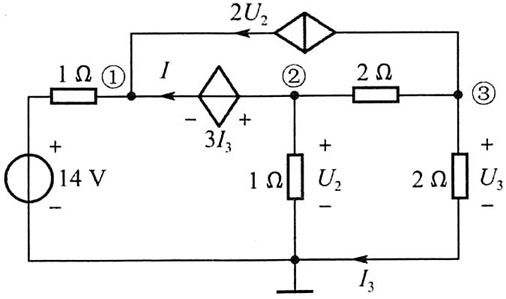
解：
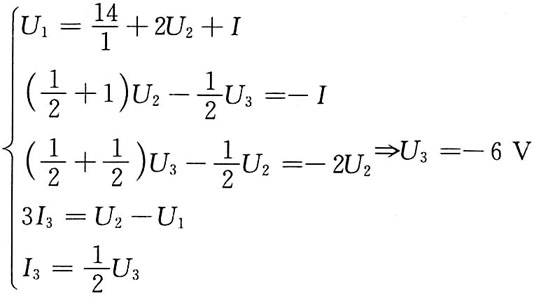
9. 对称三相电路如下图所示，顺序电源线电压
，线电流
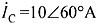
。试求该对称三相电路消耗的总平均功率P。
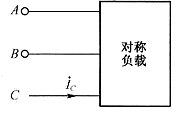
解：根据对称三相电路电压电流之间的关系可得：
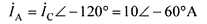
若负载为Y型连接，则有：
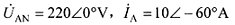
因此，对称三相电路消耗的总平均功率为：
P=3×220×10×cos[0°-(-60°)]=3300=3.3kW
10. 试求下图所示二端口网络的Z参数。
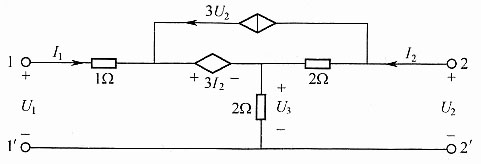
解：2-2'断开时，I
2=0，此时电路如下图所示。
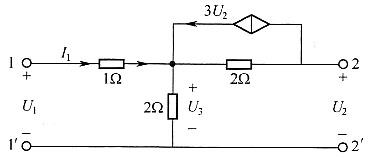
u
3=i
1×2
根据分压关系可得：
u
1=i(2+1)=3i
1 则：Z
11=3
2-2'端口电压为：
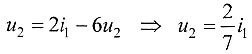
则：
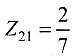
2-2'短路时，U
2=0，此时电路如下图所示。
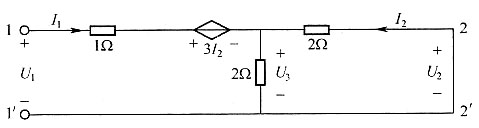
根据分流关系可得：
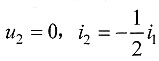
由分压关系可得：
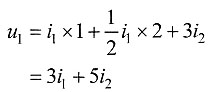
所以：Z
12=5
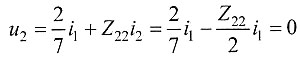
所以：
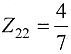
因此可得Z参数为：
则
，同理可得
时，方程简化为：
，因此则有：
深色：已答题 浅色：未答题