计算题1. 已知下图,电压表V
1的读数为32V,电压表V的读数为40V,求电压表V
2的读数。
解:
解法一:令I为参考相量I∠0°
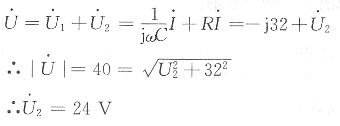
解法二:利用向量图求解。以I为参考相量I∠0°,则所作相量图如图所示,
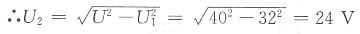
2. 下图所示正弦交流电路,已知电路的有功功率P=15W,电压有效值U
S=U
L=10V,且
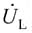
超前
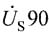
。求R、X
L、X
C及电流I。
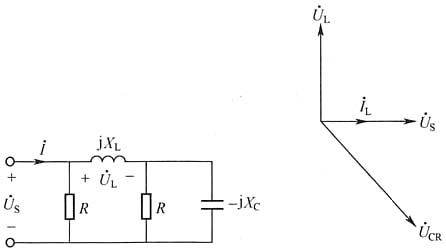
解:设

,由相量图可知:

R、X
L、X
C及电流I的解题步骤如下:
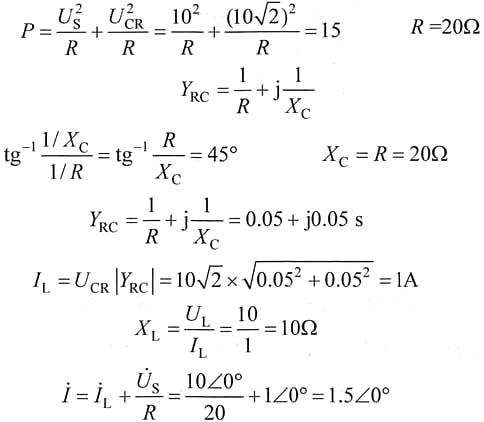
I=1.5A
3. 对图1所示电路,选一常态树,写出矩阵形式的状态方程。
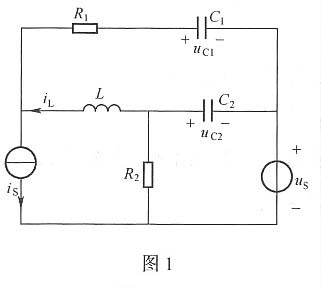
解:选取常态数(见图2):
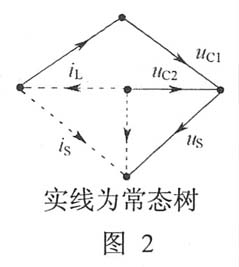
矩阵形式的状态方程为:

4. 如图所示电路中R=2Ω,直流电压源U
S=9V,非线性电阻的伏安特性
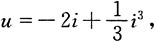
,若u
s(t)=costV,试求电流i。
解:求电路的静态工作点。令u
s(t)=0V,则U
S=RI+U
把非线性电阻的伏安特性

代入上式,可得
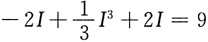
求解方程可得静态工作点
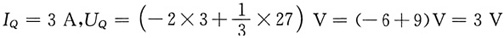
所以工作点处的动态电阻为
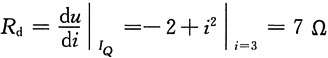
作小信号等效电路如下图所示,且
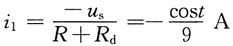
解得
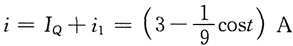
5. 求如图所示电路中的u、i。
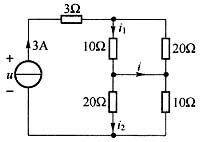
解:根据电阻并联电流分流公式,可得:
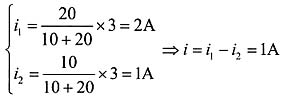
根据KVL,可得:u=3×3+2×10+1×20=49V
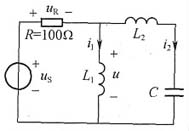
6. 电路如图所示,u
S(t)=[100+180cosω
1t+50cos2ω
1t]V,ω
1L
1=90Ω,ω
1L
2=30Ω,

,试求u
R(t)、u(t)、i
1(t)和i
2(t)。
解:(1)直流作用时,U
S(0)=100V,则有:
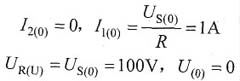
(2)基波作用,
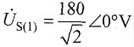
,等效相量模型如图(a)所示:
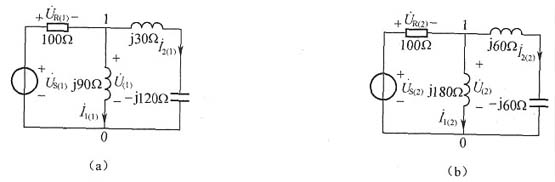
由于Y
10(1)=0,右边部分发生并联谐振,相当于开路,因此有:
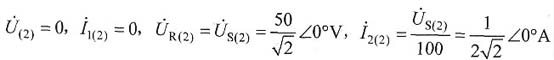
(3)二次滤波作用,
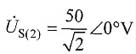
,等效相量模型如图(b)所示。
由于Z
10(2)=0,右边部分发生串联谐振,相当于短路,因此有:
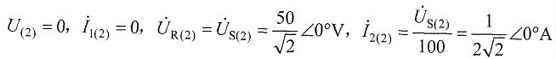
所以有:

7. 电路如图1所示,D为理想二极管,试求:
(1)ab以左端口的戴维南等效电路。
(2)求U
ab及I的值。
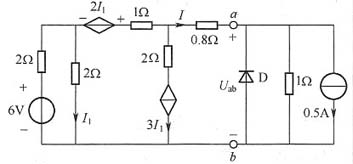
图1
解:根据题意可知,要计算ab左端口的戴维南等效电路,由于电路包含受控源,所以可以采用开路短路法求解。
(1)开路电压计算。电路如图2所示。
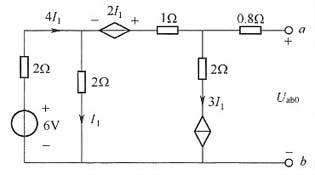
图2
根据上述电路,可得回路电压方程为:
4I
1×2+2×I
1=6
求解得:
I
1=0.6A
因此,开路电压为:
U
ab0=-3I
1+2I
1+2I
1=0.6V
可利用加压法计算等值电阻,此时内部电压源相当于短路,因此计算电路如图3所示。
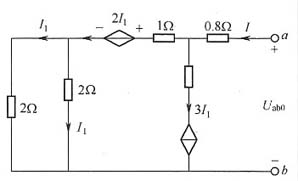
图3
根据上图,利用分流原理可得:
I=5I
1 U=0.8I+2I
1+2I
1+2I
1=10I
1 因此,等效电阻R
0的值为:

故可得出戴维南等效电路如图4所示。
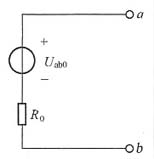
图4
(2)可对原电路进行化简,化简后如图5所示。
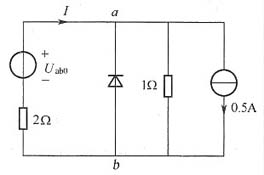
图5
设二极管截止,则可得出:

整理上式,可得出U
ab的值为:
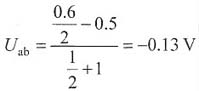
从计算结果可知a点电位低于b点电位,故二极管导通,所以U
ab=0,此时可求出I的值为:
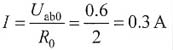
8. 求图1所示电路中的I
L。
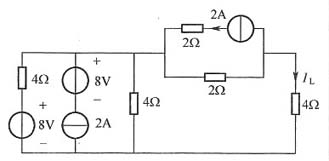
图1
解:一般等效电路如图2所示。
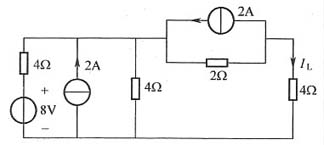
图2
先等效左半部分电路如图3所示。
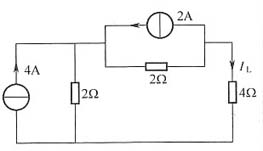
图3
整个电路的戴维南等效电路如图4所示。
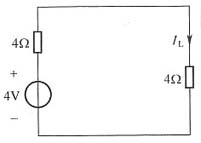
图4
可得:
I
L=0.5A
9. 试求出下图电路在正弦激励情况下该二端口网络的Z参数。
解:设正弦激励源的角频率为ω,将受控电流源等效变换为受控电压源,得下图。按此图列KVL,KCL方程,消去

,即得
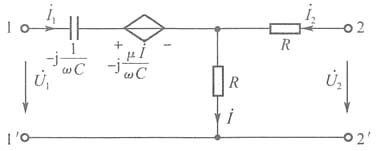
由此即可得出二端口网络的Z参数矩阵为
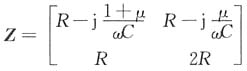
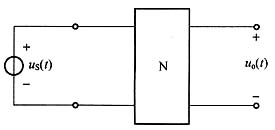
10. 如图所示电路,N为线性RC网络。已知在同一初始条件下,当u
S(t)=0时,全响应u
o(t)=-e
-10tε(t)V;当u
S(t)=12ε(t)V时,全响应u
o(t)=(6-3e
-10t)ε(t)V;若u
S(t)=6e
-5tε(t)V且初始状态仍不变时,求全响应u
o(t)。
解:由题知,u
o的零输入响应即为u
o(t)=-e
-10tε(t)V,现求u
o的网络函数H(S)。
利用拉氏变换,当u
S(S)=0时:
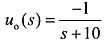
当
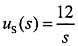
时:
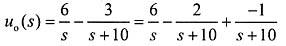
此时的零状态响应为
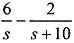
,所以:
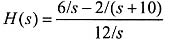
当
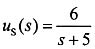
时,零状态响应为H(S)U
S(S)=R(S),即此时的零状态响应为:

此时R(t)=4e
-5t-2e
-10t,所以,全响应为:
u
o(t)=(4e
-5t-2e
-10t-e
-10t)ε(t)=(4e
-3t-3e
-10t)ε(t)V