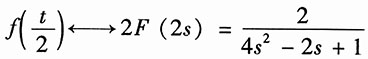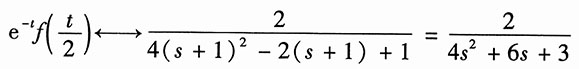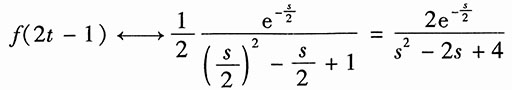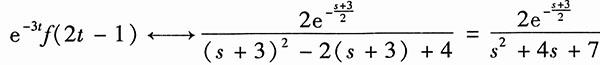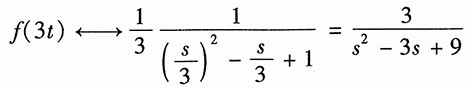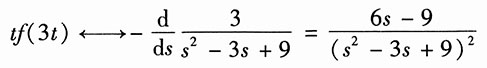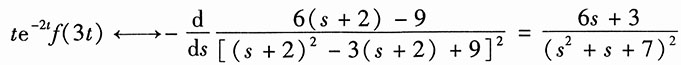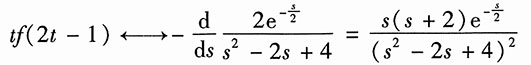计算题1. 描述某LTI离散系统的差分方程为
y(k)-y(k-1)-2y(k-2)=f(k)
已知y(-1)=-1,
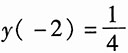
,f(k)=ε(k),求该系统的零输入响应y
zi(k),零状态响应y
zs(k)及全响应y(k)。
解:设y(k)的Z变换为Y(z),f(k)的Z变换为F(z)。对差分方程取单边Z变换,利用移序特性,得
Y(z)-[z
-1Y(z)+y(-1)]-2[z
-2Y(z)+z
-1y(-1)+y(-2)]=F(z)
解得
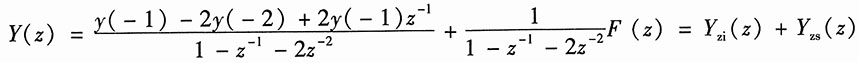
其中
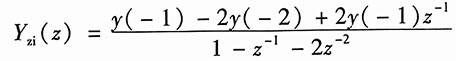
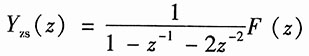
将初始状态y(-1)=-1,
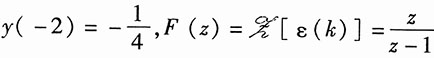
代入并整理,得
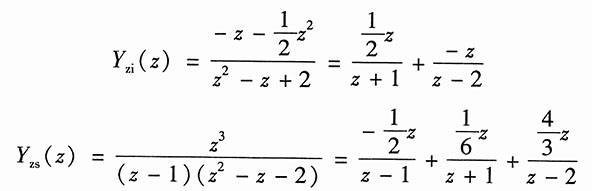
对以上两式取逆变换,得系统的零输入响应和零状态响应分别为
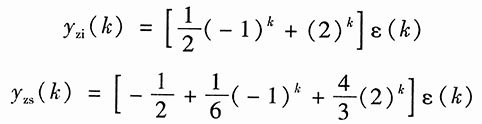
系统的全响应为
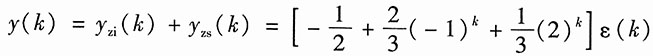
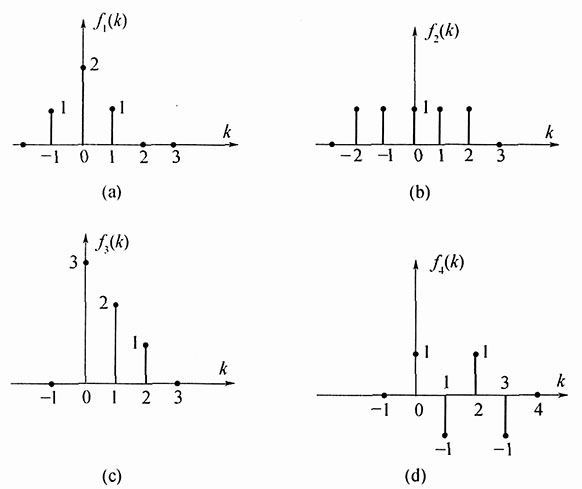
2. f
1(k)*f
2(k);
解:
f1(k)*f2(k)
=[δ(k+1)+2δ(k)+δ(k-1)]*[ε(k+2)-ε(k-3)]
=ε(k+3)+2ε(k+2)+ε(k+1)-ε(k-2)-2ε(k-3)-ε(k-4)
3. f
2(k)*f
3(k);
解:f2(k)*f3(k)
=[ε(k+2)-ε(k-3)]*[3δ(k)+2δ(k-1)+δ(k-2)]
=3ε(k+2)+2ε(k+1)+ε(k)-3ε(k-3)-2ε(k-4)-ε(k-5)
4. f
3(k)*f
4(k);
解:f3(k)*f4(k)
=[3δ(k)+2δ(k-1)+δ(k-2)]*[δ(k)-δ(k-1)+δ(k-2)-δ(k-3)]
=3δ(k)-3δ(k-1)+3δ(k-2)-3δ(k-3)+2δ(k-1)-2δ(k-2)+2δ(k-3)-2δ(k-4)+δ(k-2)-δ(k-3)+δ(k-4)-δ(k-5)
=3δ(k)-δ(k-1)+2δ(k-2)-2δ(k-3)-δ(k-4)-δ(k-5)
5. [f
2(k)-f
1(k)]*f
3(k)。
解:[f2(k)-f1(k)]*f3(k)
=[δ(k+2)-δ(k)+δ(k-2)]*[3δ(k)+2δ(k-1)+δ(k-2)]
=3δ(k+2)+2δ(k+1)-2δ(k)-2δ(k-1)+2δ(k-2)+2δ(k-3)+δ(k-4)
6. 一个LTI系统的频率响应为
若输入
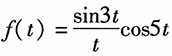
,求该系统的输出y(t)。
解:

取τ=6,所以
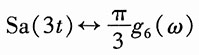
又因为
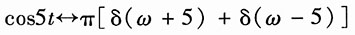
由频域卷积定理,得
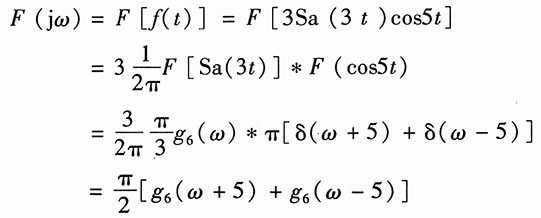
所以
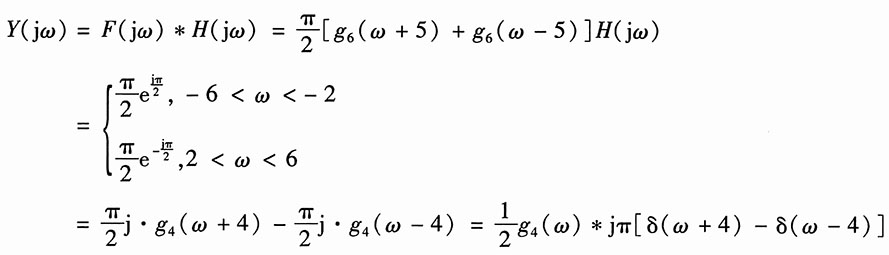
因为
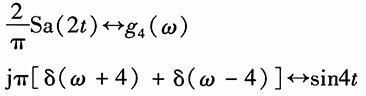
所以
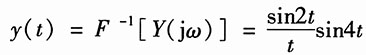
7. f(k)=h(k)=ε(k);
解:
yf(k)=h(k)*f(k)
=ε(k)*ε(k)=(k+1)ε(k)
8. f(k)=ε(k),h(k)=δ(k)-δ(k-3);
解:yf(k)=f(k)*h(k)
=ε(k)*[δ(k)-δ(k-3)]
=ε(k)-ε(k-3)
9. f(k)=h(k)=ε(k)-ε(k-4);
解:yf(k)=f(k)*h(k)
=[ε(k)-ε(k-4)]*[ε(k)-ε(k-4)]
=ε(k)*[δ(k)-δ(k-4)]*δ(k)*[δ(k)-δ(k-4)]
=(k+1)ε(k)*[δ(k)-2δ(k-4)+δ(k-8)]
=(k+1)ε(k)-2(k-3)ε(k-4)+(k-7)ε(k-8)
10. f(k)=(0.5)
kε(k),h(k)=ε(k)-ε(k-5)。
解:
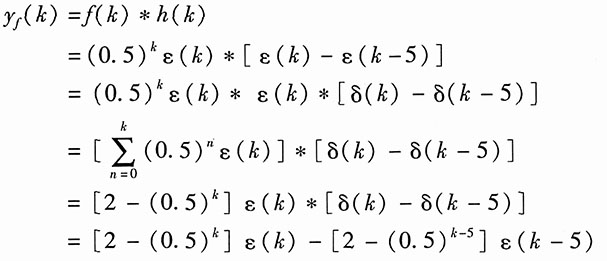
11. 如图所示的复合系统由3个子系统组成,已知子系统2的单位序列响应h
2(k)=(-1)
kε(k),子系统3的系统函数
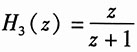
,当输入f(k)=ε(k)时复合系统的零状态响应y
zs(k)=3(k+1)ε(k)。求子系统1的单位序列响应h
1(k)。
解:令
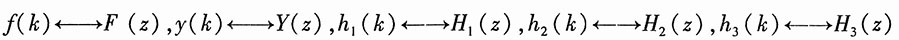
。
设子系统1的输入为X(z),由左端加法器可列出方程:
X(z)=F(z)+H
1(z)H
2(z)X(z)
即
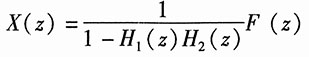
由右端加法器可列出方程:
Y(z)=X(z)H
1(z)-X(z)H
3(z)=[H
1(z)-H
3(z)]X(z)
从以上两式中消去中间变量X(z),可得
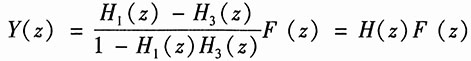
式中复合系统的系统函数为
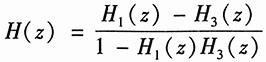
又由已知可得
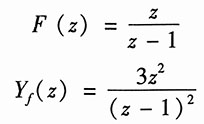
可解系统函数为
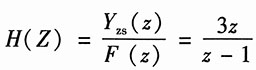
即有
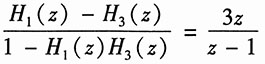
将
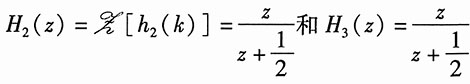
代入得
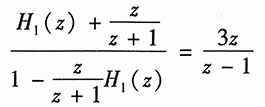
可以解得
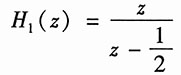
对上式取逆变换,得子系统1的单位序列响应为
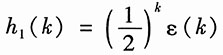
12. 某一阶LTI离散系统,其初始状态为x(0)。已知当激励为f(k)时,其全响应为
y
1(k)=ε(k)
若初始状态不变,激励为-f(k)时,其全响应为
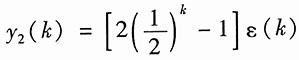
求若初始状态为2x(0),激励为4f(k)时,系统的全响应。
解:设初始状态为x(0)引起的零输入响应为y
x(k),激励为f(k)引起的零状态响应为y
f(k),由已知条件,得
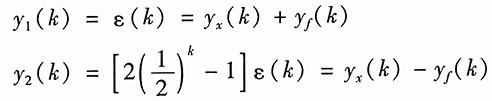
联立以上两式,得
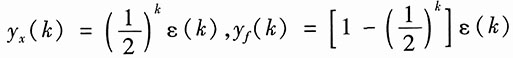
所以利用LTI离散系统性质,当初始状态为2x(0),激励为4f(k)时,系统的全响应为

13. 下图所示系统,若激励
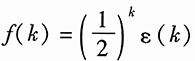
,求系统的零状态响应。
解:
由图知左、右迟延单元的输出分别为y(k-1)、y(k-2),由加法器的输出可得
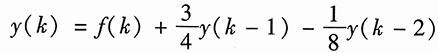
即
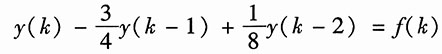
(1)
所以系统的单位序列响应满足方程
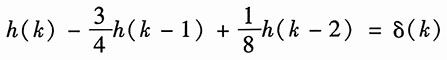
(2)
且
h(-1)=h(-2)=0
系统的特征方程为
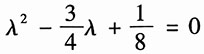
系统的特征根为
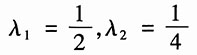
解式(2),得
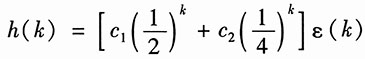
由式(2)可得
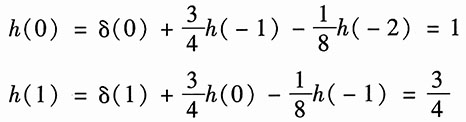
将h(0)、h(1)代入上式,得

所以
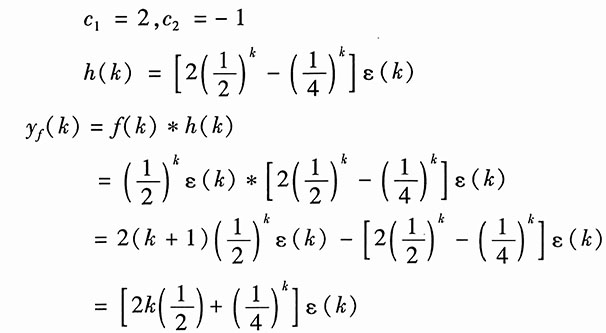
14. 已知某一阶LTI系统,当初始状态y(-1)=1,输入f
1(k)=ε(k)时,其全响应y
1(k)=2ε(k);当初始状态y(-1)=-1,输入

时,其全响应y
2(k)=(k-1)ε(k)。求输入
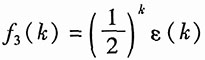
时的零状态响应。
解:设当初始状态y(-1)=1时,系统零输入响应为y
zi(k),则根据LTI系统性质,当初始状态y(-1)=-1时,系统零输入响应为-y
zi(k)。
所以当初始状态y(-1)=1,输入f
1(k)=ε(k)时,其全响应为
y
1(k)=y
zi(k)+y
zs(k)=y
zi(k)+h(k)*f
1(k)=2ε(k) (1)
当初始状态y(-1)=-1,输入

时,其全响应为
y
2(k)=-y
zi(k)+y
zs(k)=-y
zi(k)+h(k)*f
2(k)=(k-1)ε(k) (2)
由式(1)、式(2),得
h(k)*[f
1(k)+f
2(k)]=2ε(k)+(k-1)ε(k)=(k+1)ε(k) (3)
因为
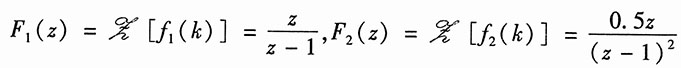
所以对式(3)两边取Z变换可得
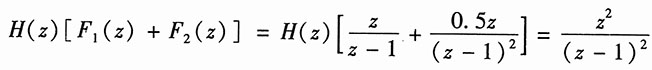
解得
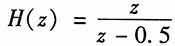
又因为
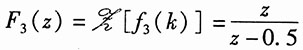
,所以其零状态的象函数为
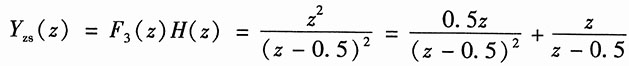
取逆变换得系统的零状态为
y
zs(k)=(k+1)(0.5)
kε(k)
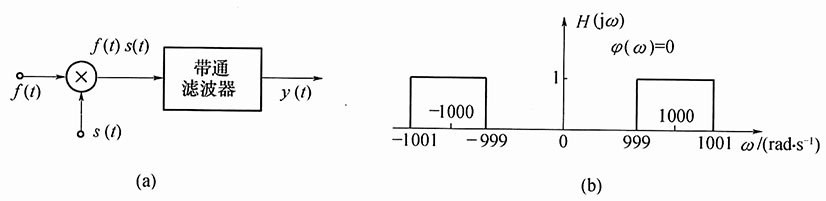
15. 如图(a)的系统,带通滤波器的频率响应如图(b)所示,其相频特性φ(ω)=0,若输入为
求输出信号y(t)。
解:因为
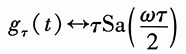
由对称性,得
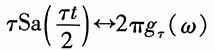
所以
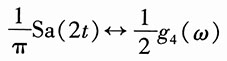
即
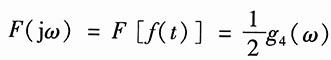
设乘法器输出为x(t),即x(t)=f(t)s(t)。
则
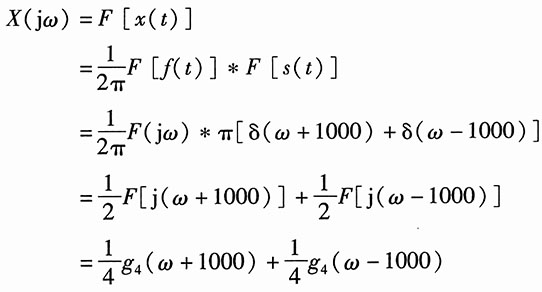
所以
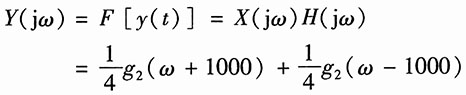
由
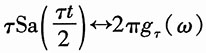
及频移特性,得
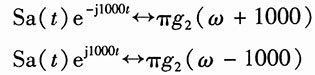
所以利用线性特性,得
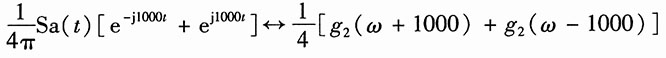
即
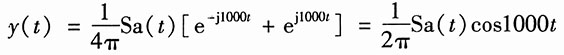
16. 图(a)所示为抑制载波振幅调制的接收系统,若输入信号为
低通滤波器的频率响应如图(b)所示,其相位特性φ(ω)=0。试求其输出信号y(t)。
解:设乘法器输出为x(t),即x(t)=f(t)·s(t)。
由上题可知
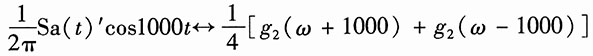
所以
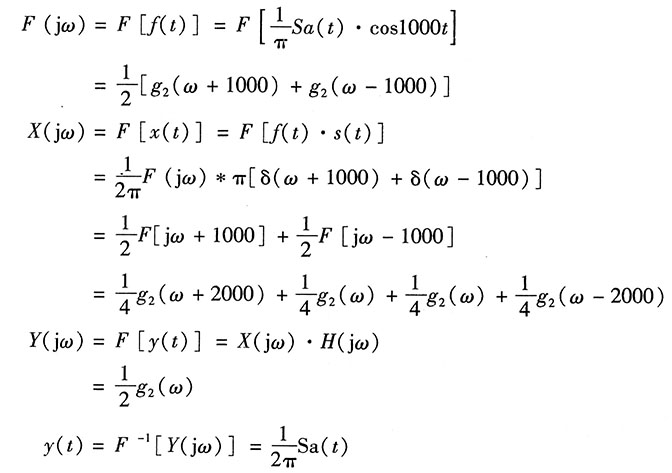
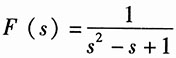 ,求下列函数的象函数。
,求下列函数的象函数。
17.
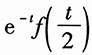
解:已知因果函数
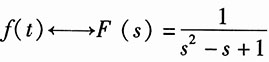
。
利用尺度变换,得
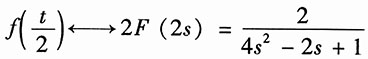
再利用复频域特性,得
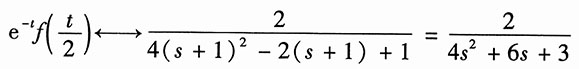
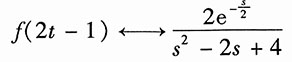
18. e
-3tf(2t-1);
解:利用时移特性,得

再利用尺度变换,得
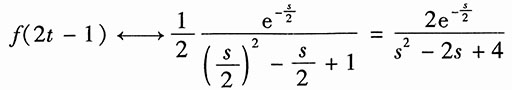
再利用复频域特性,得
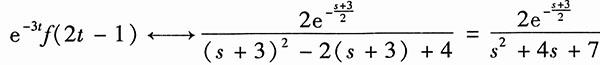
19. te
-2tf(3t);
解:利用尺度变换,得
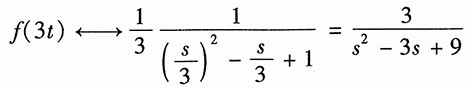
然后利用复频域微分特性,得
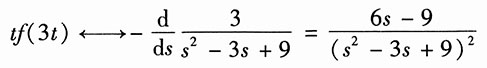
再利用复频域特性,得
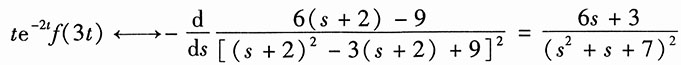
20. tf(2t-1)。
解:由第二小题,得
利用复频域微分特性,得
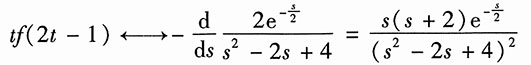
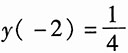 ,f(k)=ε(k),求该系统的零输入响应yzi(k),零状态响应yzs(k)及全响应y(k)。
,f(k)=ε(k),求该系统的零输入响应yzi(k),零状态响应yzs(k)及全响应y(k)。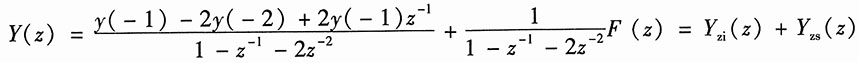
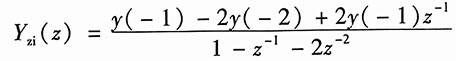
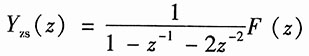
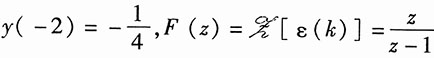 代入并整理,得
代入并整理,得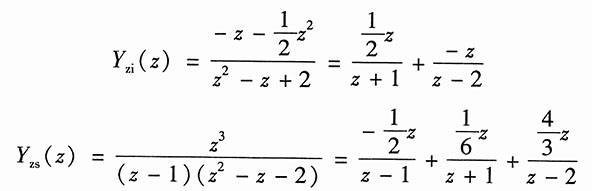
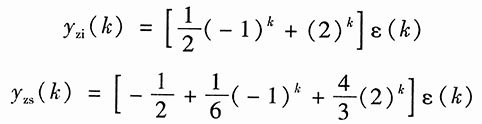
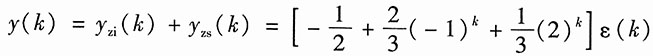
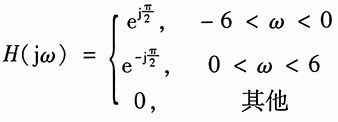
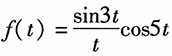 ,求该系统的输出y(t)。
,求该系统的输出y(t)。
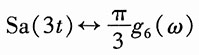
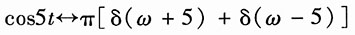
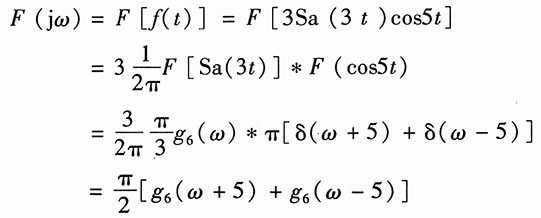
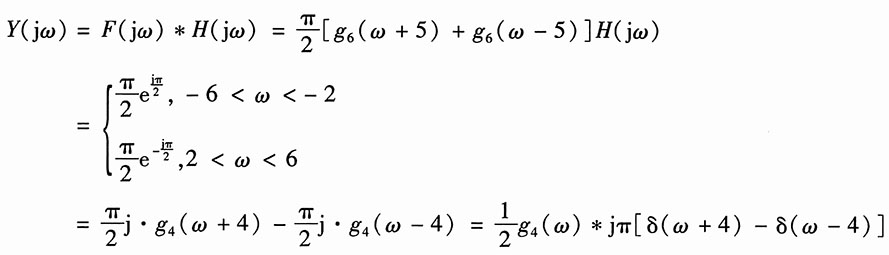
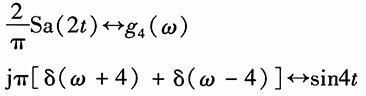
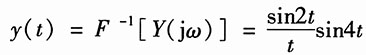
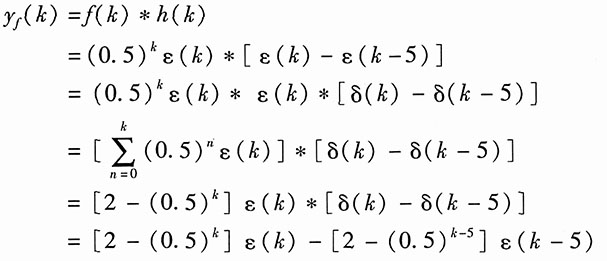
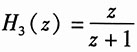 ,当输入f(k)=ε(k)时复合系统的零状态响应yzs(k)=3(k+1)ε(k)。求子系统1的单位序列响应h1(k)。
,当输入f(k)=ε(k)时复合系统的零状态响应yzs(k)=3(k+1)ε(k)。求子系统1的单位序列响应h1(k)。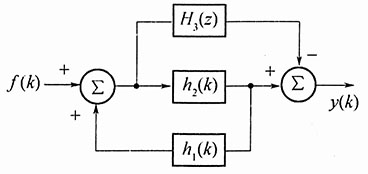
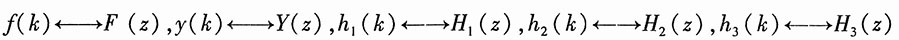 。
。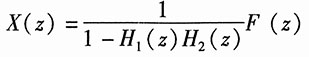
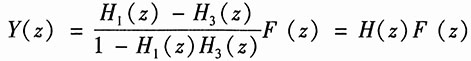
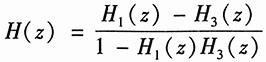
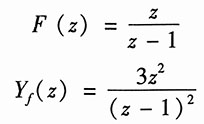
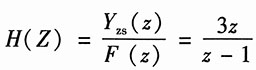
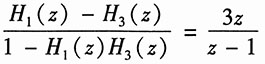
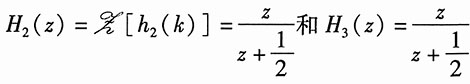 代入得
代入得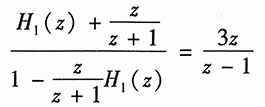
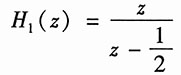
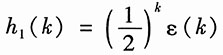
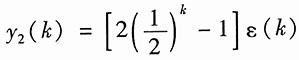
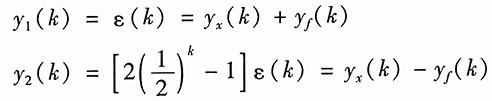
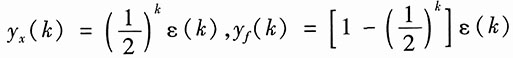

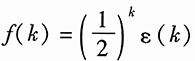 ,求系统的零状态响应。
,求系统的零状态响应。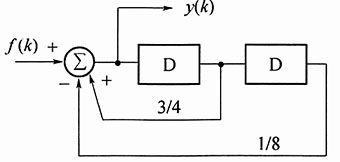
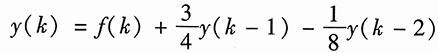
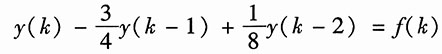 (1)
(1)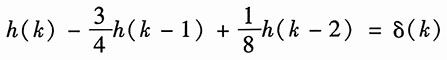 (2)
(2)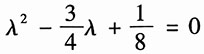
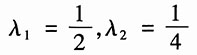
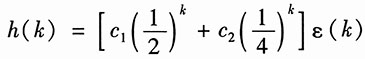
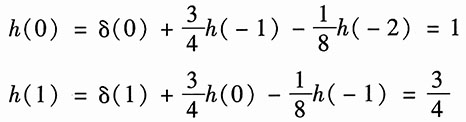

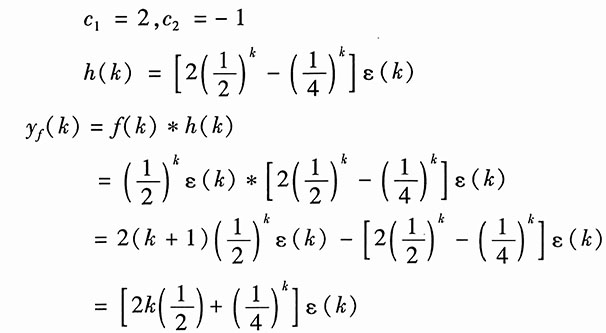
 时,其全响应y2(k)=(k-1)ε(k)。求输入
时,其全响应y2(k)=(k-1)ε(k)。求输入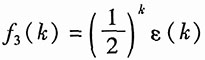 时的零状态响应。
时的零状态响应。 时,其全响应为
时,其全响应为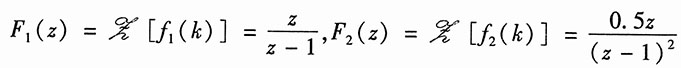
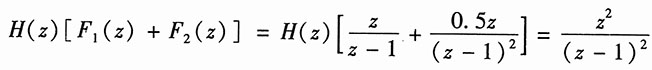
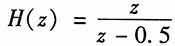
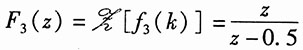 ,所以其零状态的象函数为
,所以其零状态的象函数为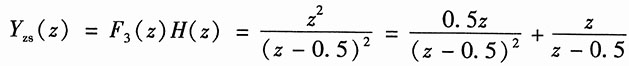
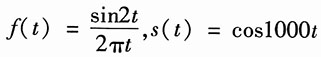

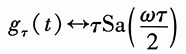
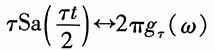
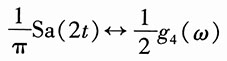
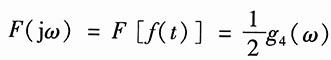
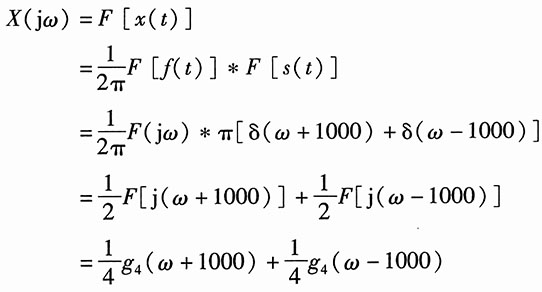
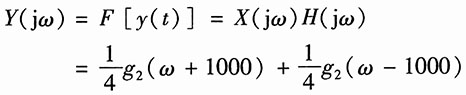
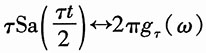 及频移特性,得
及频移特性,得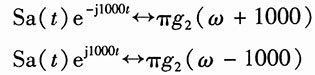
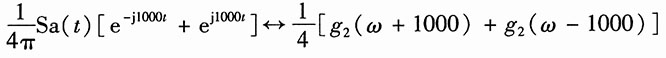
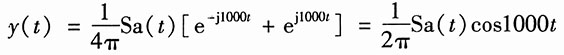
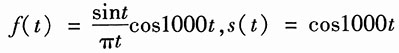
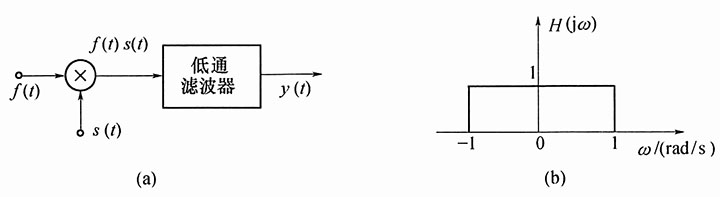
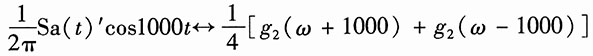
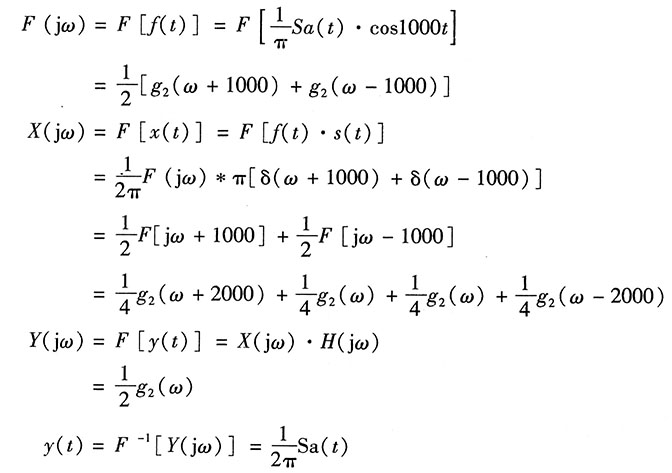
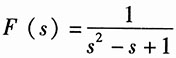 ,求下列函数的象函数。
,求下列函数的象函数。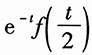
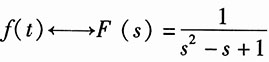 。
。