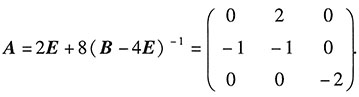一、数学单项选择题1. 不定积分
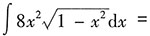
______.
A.
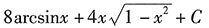
B.
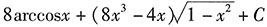
C.
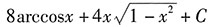
D.
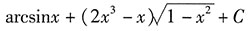
A B C D
D
[解析] 换元法:
第一步,换元积分.
设
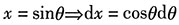
,则
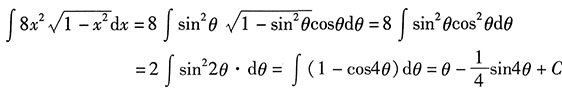
第二步,还原.
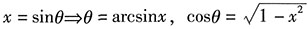
,则
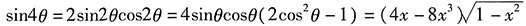
故
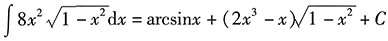
综上所述,答案是D.
2. 设随机变量X服从参数为λ(λ>0)的指数分布,假设E(X
2+2X)=4,则P[X>D(X)]=______.
A B C D
C
[解析]
由数学期望的性质可知E(X
2+2X)=E(X
2)+2E(X).
由于X~E(λ),可知
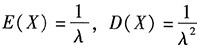
.
由方差的计算公式D(X)=E(X
2)-[E(X)]
2可知
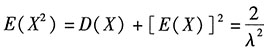
.
故有
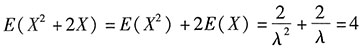
,解得λ=1或
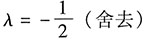
.
所以λ=1.
因此X的概率密度为
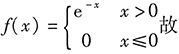
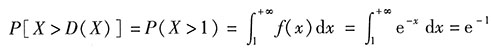
,应选C.
3. 设区域D由x=a,x=b(b>a),y=f(x),y=g(x)所围成,则区域D的面积为______.
A.
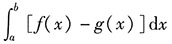
B.
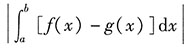
C.
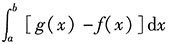
D.
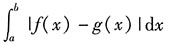
A B C D
D
[解析] 由定积分的几何意义可得D的面积为
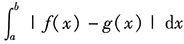
.
综上所述,答案是D.
4. n维列向量组α
1,…,α
m(m<n)线性无关,则n维列向量组β
1,…,β
m线性无关的充分必要条件为______.
- A.向量组α1,…,αm可由向量组β1,…,βm线性表示
- B.向量组β1,…,βm可由向量组α1,…,αm线性表示
- C.向量组α1,…,αm与向量组β1,…,βm等价
- D.矩阵A=(α1,…,αm)与矩阵B=(β1,…,βm)等价
A B C D
D
[解析]
A选项是充分非必要条件,具体分析如下:
①A是充分条件:
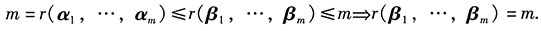
②A是非必要条件:反例:
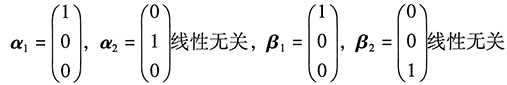
,
但α
1,α
2不能由β
1,β
2线性表示.
B选项是既非必要也非充分条件,具体分析如下:
①B是非必要条件:反例:
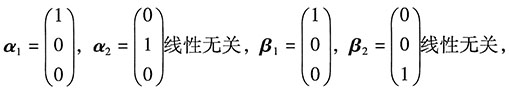
但β
1,β
2不能由α
1,α
2线性表示.
②B是非充分条件:反例:

β
1,β
2可由α
1,α
2线性表示,但β
1,β
2线性相关.
C选项是充分非必要条件,具体分析如下:
①C是充分条件:r(β
1,…,β
m)=r(α
1,…,α
m)=m.
②C是非必要条件:反例:
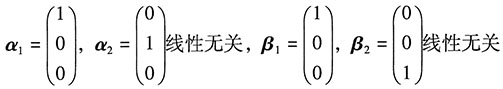
,
但α
1,α
2不能由β
1,β
2线性表示,则α
1,α
2与β
1,β
2不等价.
D选项是充分必要条件,具体分析如下:
向量组β
1,…,β
m线性无关

综上所述,答案是D.
7. 设
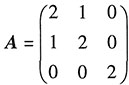
,若AB=A+E,则B=______.
A.
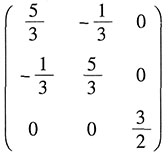
B.

C.

D.
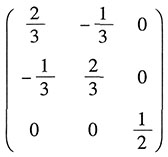
A B C D
A
[解析]
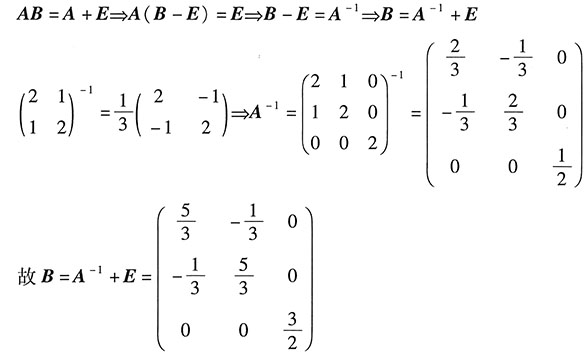
综上所述,答案是A.
A
-1也可以用初等变换求得,请考生自己演练一遍.
9. 当x→1时,函数
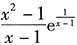
的极限______.
A B C D
D
[解析] 对于函数在给定点x
0的极限是否存在需要判定左极限x→x
0-和右极限x→x
0+是否存在且相等,若相等,则函数在点x
0的极限是存在的.
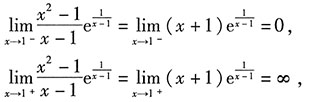
0≠∞,故当x→1时函数没有极限,也不是∞.综上所述,答案是D.
上述题目说明了无界量和无穷大量的区别与联系:在某一极限过程中,函数f(x)无界只要求函数在该变化过程中至少有部分点的函数值趋近于无穷即可,而函数f(x)无穷大则要求该变化过程中函数在所有点上的函数值都趋近于无穷.因此,无穷大量一定无界,但无界量不一定为无穷大量.
例如本题,当x→1
+时,函数是无穷大量;但如果讨论的极限过程是x→1,函数就不是无穷大量.因为x→1包含x→1
+与x→1
-,而x→1
-时函数的极限是0.因此在x→1时,函数只是在“部分点”上趋近于无穷,也即函数是无界的但不是无穷大量.
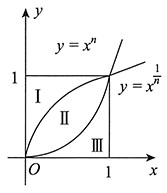
10. 设y=x
n与
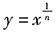
(n>1)相交于第一象限(如图所示),若三个区域Ⅰ、Ⅱ、Ⅲ的面积相等,则n=______.
A.2
B.
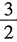
C.3
D.
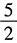
A B C D
A
[解析] 如图所示,
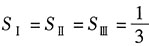
.
根据定积分可知
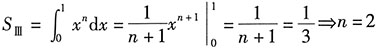
.
综上所述,答案是A.
二、数学计算题1. 求
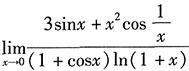
.
解:
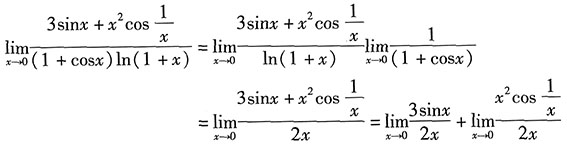
由于
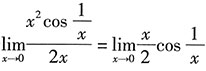
,这是无穷小与有界量的乘积,故
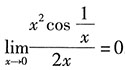
.
因此,
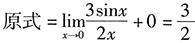
.
[解析] 本题又用到了四则运算法则中的乘法公式
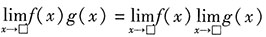
对极限式进行化简,与加法类似的是,该公式成立的充要条件也是
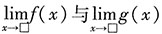
均存在.一般来说,如果
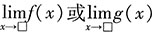
存在且不为0,则另一个也存在,因此我们有:当
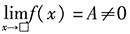
时,
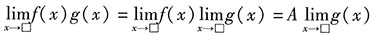
(此时,当
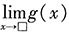
不存在时,原极限
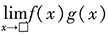
也不存在).
2. 设随机变量X服从参数为1的指数分布,Y=sinX,求E(X+Y),D(Y).
解:第一步,写出随机变量X的概率密度.
X服从参数为1的指数分布
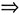
X的概率密度为
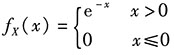
第二步,求随机变量的数字特征值.
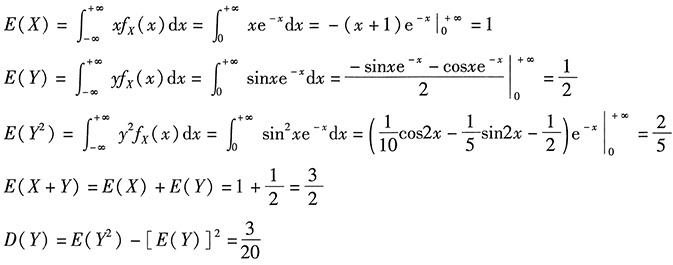
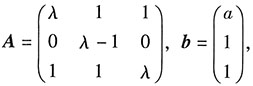 已知线性方程组AX=b有两个不同的解,
已知线性方程组AX=b有两个不同的解,3. 求λ,a.
解:第一步,分析与转化.
由“线性方程组AX=b有两个不同的解”可得:
非齐次线性方程组AX=b有无数个解
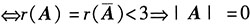
.
第二步,运算.
线性方程组AX=b有两个不同的解,则

当λ=1时,
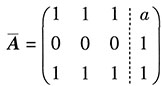
,则

,所以λ=1不成立.
当λ=-1时,
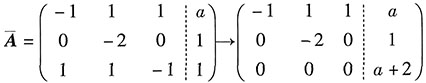
,
因为AX=b有解,所以
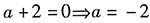
.
综上,λ=-1,a=-2.
4. 求方程AX=b的通解.
原方程与以下方程组同解
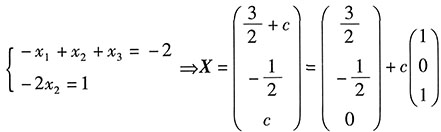
,其中c为任意常数.
[解析] 非齐次线性方程组的判解定理:
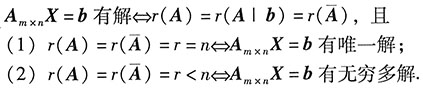
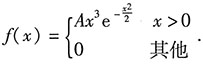
(编者注:考试时只做第一小题和第二小题两问,本题提出了4问只是为了展示命题时的完整设问模式,便于考生掌握概率命题中的套路,做好相应的考前准备!)5. 求常数A.
解:
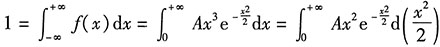
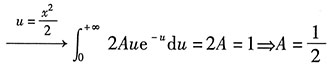
6. 求X的分布函数.
解:X的分布函数
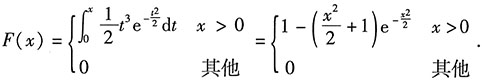
7. 求概率P(-2≤X≤4);
解:P(-2≤X≤4)=F(4)-F(-2)=F(4)=1-9e-8.
8. 求E(X
2).
解:
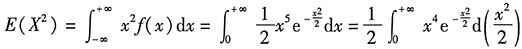
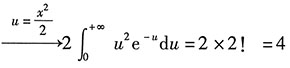
[解析] (1)概率密度与概率分布函数之间的转化实际上就是积分与导数之间的转化.
(2)
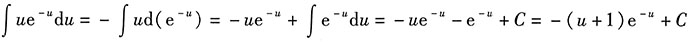
这一结论在求解第一问时用到,
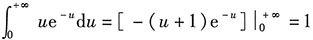
.
在求解第二问时也用到,令
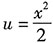
,则
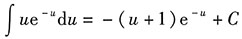
变为:
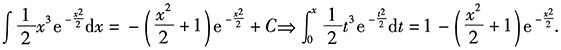
(3)更一般地,
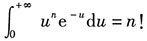
,这个结论在考试中经常用到,请考生熟记.
9. 设z=u
φ,
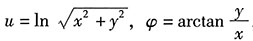
,求dz.
解:第一步,分析函数的复合结构,画出链条结构图,如图所示:
第二步,求图中每条线所表示的偏导数:
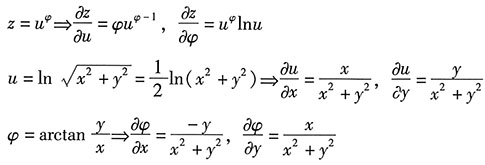
第三步,根据上图对偏导数进行复合:
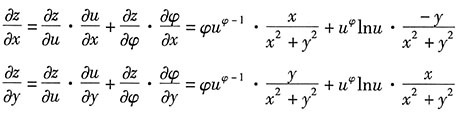
第四步,根据偏导数与全微分的关系写出全微分:
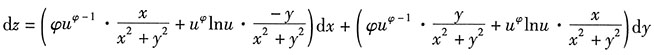
[解析] 本题揭示了使用偏导数求全微分的关键和窍门,请考生好好体会.
对比:使用全微分求偏导数的关键和窍门,在应试中偏导数和全微分二者可以“互相借力”.
10. 计算不定积分
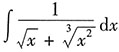
.
解:第一步,换元.
设x=u
6,则dx=6u
5du
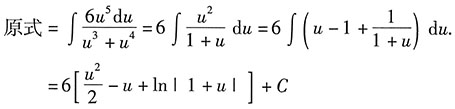
第二步,还原.
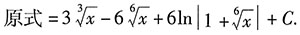
[解析] 积分式中含有多个根式的换元技巧:最小公倍数技巧.
11. 设随机变量X的概率密度为
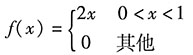
以Y表示对X的三次独立重复观察中事件
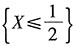
出现的次数,求P{Y=2}.
解:已知随机变量X的概率密度,所以概率
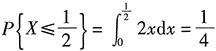
,求得二项分布的概率参数后,故
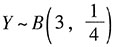
.
由二项分布的概率计算公式,所求概率为

.
12. 求曲线y=x
3-3x
2+3x+1在其拐点处的切线方程.
解:因为y=x3-3x2+3x+1,所以y'=3x2-6x+3,y"=6x-6,
令y"=0,则x=1.所以拐点为(1,2).
从而,y'|x=1=0,故切线方程为y=2.
13. 若随机变量X服从标准正态分布,若Y=X
3,求Y的概率密度、期望.
解:第一步,根据题意写出随机变量X的密度函数:
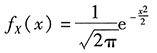
.
第二步,利用概率知识求概率密度(分布函数法).
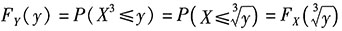
,两边对y求导:
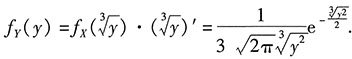
第三步,求期望(定义法).
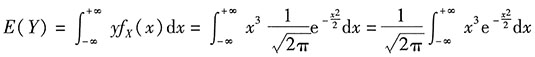
因为被积函数
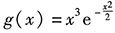
在(-∞,+∞)上是奇函数,
所以
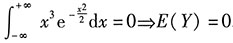
.
[解析] 考生在考场上解概率题时要能灵活地应用定积分的有关性质化简求值,如本题中利用奇函数在对称区间上的定积分为0.考试中与正态分布相关的重要的积分公式归纳小结如下:
(1)
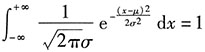
,特别地,

.
(2)

,特别地,
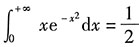
.
(3)
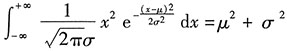
,特别地,

.
(4)针对考生在备考中相似公式容易混淆这一问题,请考生对比复习下面的公式:
Γ函数的性质:Γ(γ+1)=γΓ(γ),其中
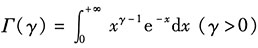
.
特别地,
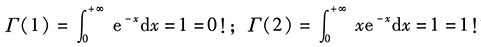
;
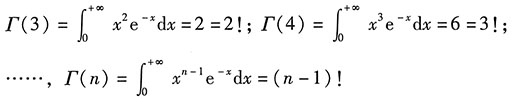
14. 证明:矩阵A-2E可逆.
证:由
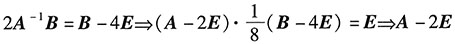
可逆,
且
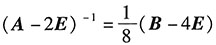
.
15. 若
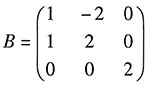
,求矩阵A.
解:由第一小题得
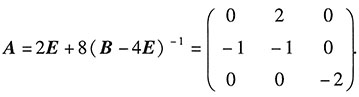
 ______.
______.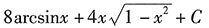
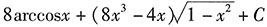
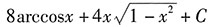
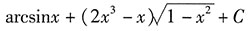
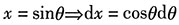 ,则
,则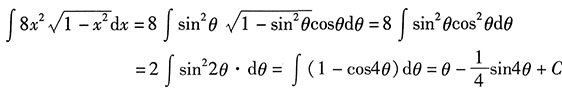
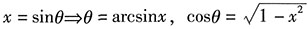 ,则
,则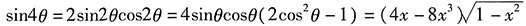
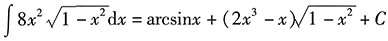
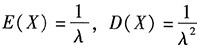 .
.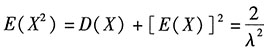 .
.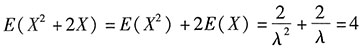 ,解得λ=1或
,解得λ=1或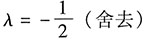 .
.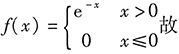
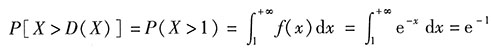 ,应选C.
,应选C.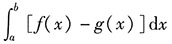
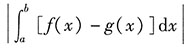
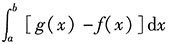
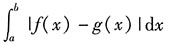
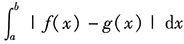 .
.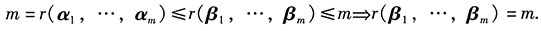
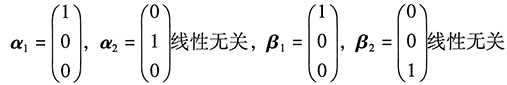 ,
,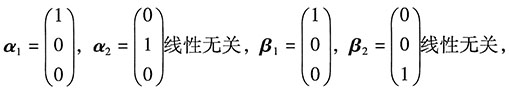

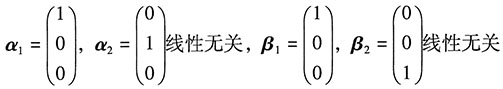 ,
,
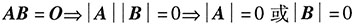 ,
,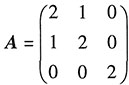 ,若AB=A+E,则B=______.
,若AB=A+E,则B=______.



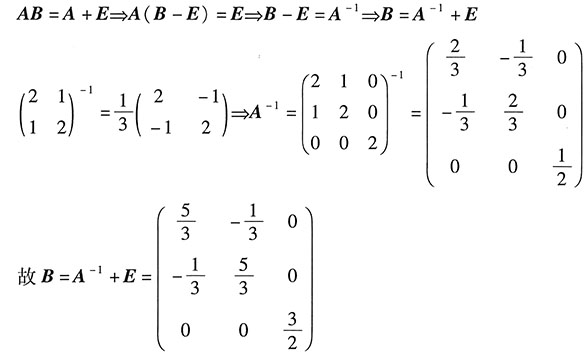
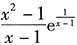 的极限______.
的极限______.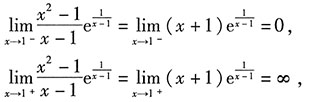
 (n>1)相交于第一象限(如图所示),若三个区域Ⅰ、Ⅱ、Ⅲ的面积相等,则n=______.
(n>1)相交于第一象限(如图所示),若三个区域Ⅰ、Ⅱ、Ⅲ的面积相等,则n=______.
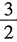
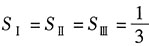 .
.
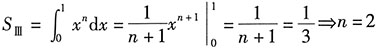 .
.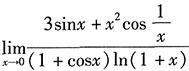 .
.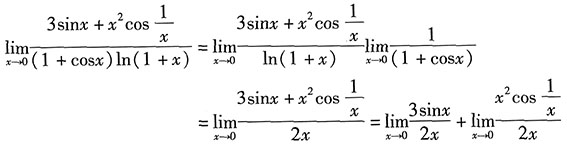
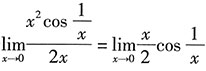 ,这是无穷小与有界量的乘积,故
,这是无穷小与有界量的乘积,故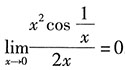 .
.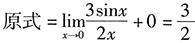 .
.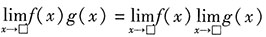 对极限式进行化简,与加法类似的是,该公式成立的充要条件也是
对极限式进行化简,与加法类似的是,该公式成立的充要条件也是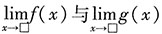 均存在.一般来说,如果
均存在.一般来说,如果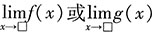 存在且不为0,则另一个也存在,因此我们有:当
存在且不为0,则另一个也存在,因此我们有:当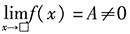 时,
时,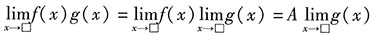 (此时,当
(此时,当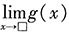 不存在时,原极限
不存在时,原极限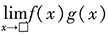 也不存在).
也不存在).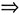 X的概率密度为
X的概率密度为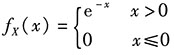
 已知线性方程组AX=b有两个不同的解,
已知线性方程组AX=b有两个不同的解,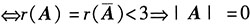 .
.
 ,则
,则 ,所以λ=1不成立.
,所以λ=1不成立.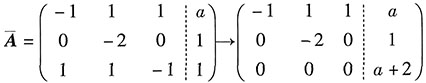 ,
,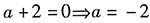 .
.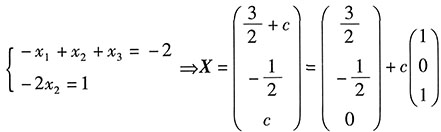 ,其中c为任意常数.
,其中c为任意常数.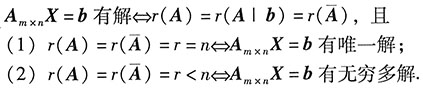
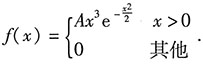
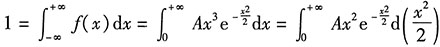
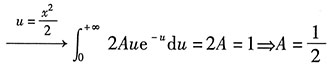
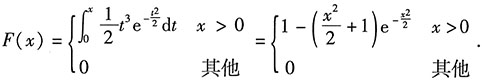
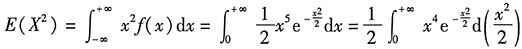
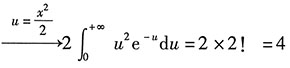
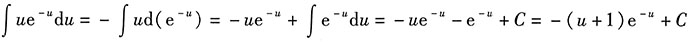
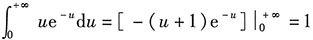 .
.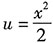 ,则
,则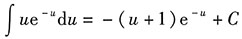 变为:
变为: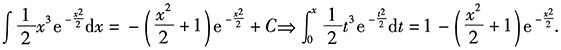
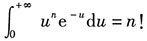 ,这个结论在考试中经常用到,请考生熟记.
,这个结论在考试中经常用到,请考生熟记.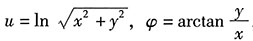 ,求dz.
,求dz.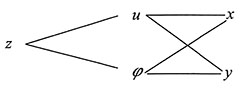
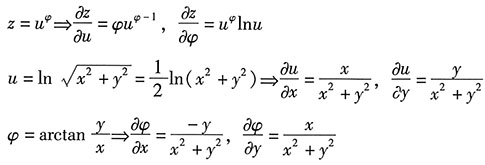
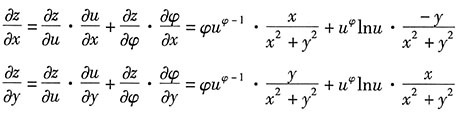
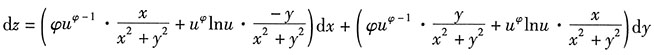
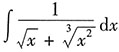 .
.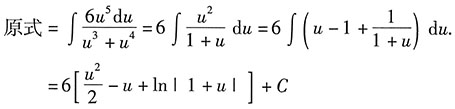
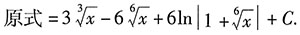
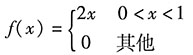
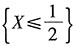 出现的次数,求P{Y=2}.
出现的次数,求P{Y=2}.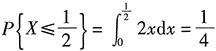 ,求得二项分布的概率参数后,故
,求得二项分布的概率参数后,故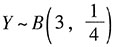 .
. .
.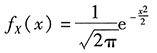 .
.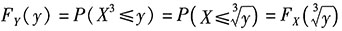 ,两边对y求导:
,两边对y求导: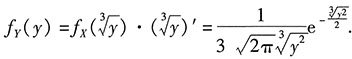
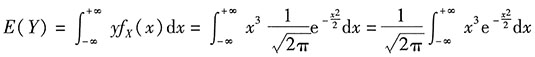
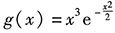 在(-∞,+∞)上是奇函数,
在(-∞,+∞)上是奇函数,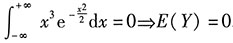 .
.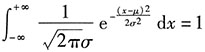 ,特别地,
,特别地, .
. ,特别地,
,特别地,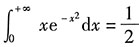 .
.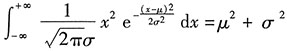 ,特别地,
,特别地, .
.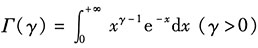 .
.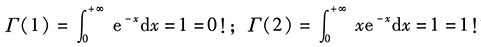 ;
;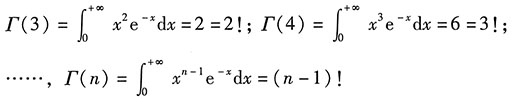
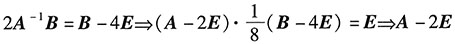 可逆,
可逆,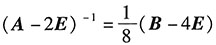 .
.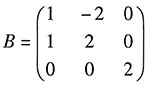 ,求矩阵A.
,求矩阵A.