一、单项选择题下列每题给出的四个选项中,只有一个选项是符合题目要求的。 二、多项选择题下列每题给出的四个选项中,至少有两个选项是符合题目要求的。 三、简答题1. 不同能力水平的人在接受同一测验时,为什么会有不同的测量误差?
就被试团体而言,整个团体内部水平的离散程度以及团体的平均水平都会影响测量信度,如果被试的能力水平相差很大时,此时的测量误差就会偏大。这是因为,所计算的信息估计值大都是以相关为基础的,而相关系数的大小往往取决于全体被试得分的分布情况。
(1)当被试团体异质(即团体内能力水平彼此差异大)时,全体被试的总分分布必然较广,那么分布位于两个端点的值可能相互抵消,以相关为基础计算出来的信度值必然会大。这就很有可能高估实际的信度值而产生测量误差。
(2)当团体内部水平相差不大(即能力水平差不多的被试位于同一水平)时,其得分分布必定会较窄,以相关为基础计算出来的信度值必然会小。这时又有可能低估真正的信度值而产生测量误差。
(3)若团体的平均水平太高或太低,同样会使测验总分的分布变窄,低估测量的真正信度而产生测量误差。
2. 抽样的基本原则是什么?
随机化是抽样研究的基本原则,指在进行抽样时,总体中每一个体是否被抽取,并不由研究者主观决定,而是每个个体按照概率原理被抽取的可能性是相等的。
3. 根据CTT的数学模型及其假设,推导关系式(3.2)
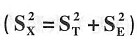
。
CTT模型及其假设
经典测验理论(CTT)假定,观察分数(记为X)与真分数(T)之间是一种线性关系,并只相差一个随机误差(记之为E)。即:X=T+E,这就是CTT的数学模型。根据这一模型,可以引申出三个相关联的假设公理:①若一个人的某种心理特质可以用平行的测验反复测量足够多次,则其观察分数的平均值会接近于真分数。即:E(X)=T,或E(E)=0。②真分数和误差分数之间的相关为零。即:ρ(T,E)=0。③各平行测验上的误差分数之间相关为零。即:ρ(E
1,E
2)=0。
(2)推导过程
关系式(3.2)为:
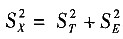
。根据CTT的数学模型及其假设,推导关系式(3.2)的过程如下:
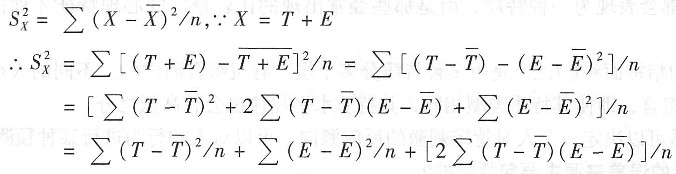
∵真分数和误差分数之间的相关为0;
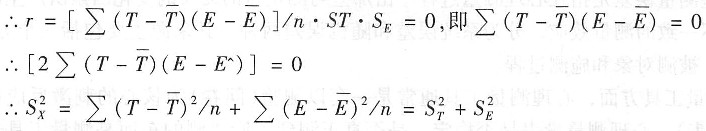
即:
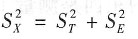
4. 根据下列方差分析表回答问题:
| 差异源 | SS | df | MS | F |
| 因素A | 6 | 2 | 3 | |
| 因素B | 12 | 1 | 12 | |
| A×B | 26 | | | |
| 残差 | 192 | 66 | 2.91 | |
| 总计 | 236 | 71 | | |
双侧检验F表(α=0.05)如下:
| 分母自由度 | 分子自由度 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 60 | 5.29 | 3.93 | 3.34 | 3.01 | 2.79 | 2.63 | 2.51 | 2.41 |
| 120 | 5.15 | 3.80 | 3.23 | 2.89 | 2.67 | 2.52 | 2.39 | 2.30 |
(1)计算交互作用A×B的自由度和它的均方值。
(2)检验因素B及A×B的显著性。
(1)对于有交互作用的双因素方差分析,A×B的自由度为(a-1)(b-1),A×B的均方值为SS
A×B/[(a-1)(b-1)]。根据本题题干信息,交互作用A×B的自由度为2;其均方值为13。交互作用A×B的自由度是2,均方值是26/2=13。
(2)因素B的F值
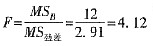
:
F<F
0.05(1,120)=5.15,所以因素B在0.05水平上不显著。
A×B的F值:

F>F
0.05(2,120)=3.80,所以A×B在0.05水平上显著。
[解析] 本题旨在考查考生对心理统计中方差分析计算公式的掌握程度。
5. 某地区过去数年统计结果,新生儿体重超过2500克,其母亲分娩时平均年龄26.5岁,今欲检验体重在2500克以下新生儿的母亲分娩时平均年龄有否显著差异,据数年资料可以假设μ=26.5,σ=0.2,若现定α=0.05,(1-β)=0.90,则至少应取多大样本?
解:μ=26.5,σ=0.2,则允许误差为
δ=Z
α/2·σ=0.392
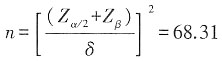
取整数为69。
答:至少应取69人。
四、综合题1. 下述一些数据,哪些是测量数据?哪些是计数数据?其数值意味着什么?
0千克(重量);89.85厘米(长度);199.2秒(时间);93.5分(分数)是测量数据。
17人(人数);25本(书本数)是计数数据。
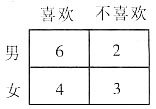
2. 下表是对一部作品的调查结果,请用精确概率及χ
2检验分析评价与性别是否有关。
解:用χ
2连续性校正公式计算。
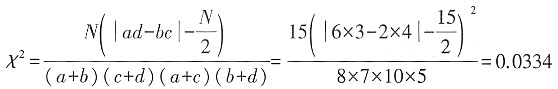
查χ
2表,df=1,
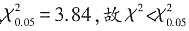
,p>0.05
答:差异不显著,即评价与性别无关。
3. 从30个白球20个黑球共50个球中随机抽取两次,问抽一黑球与一白球的概率是多少?两次皆是白球队与两次都是黑球的概率各是多少?
抽一白球与抽一黑球的概率符合古典概率。
设抽一白球的概率是P(A),抽一黑球的概率是P(B)。
抽到一个白球的概率是P(A)=0.6,抽一黑球的概率是P(B)=0.4。
抽一白球和抽一黑球的概率满足乘法定理,P(A×B)=P(A)×P(B)=0.24。
两次皆是白球的概率满足乘法定理,P(A×A)=P(A)×P(A)=0.36。
两次皆是黑球的概率满足乘法定理,P(B×B)=P(B)×P(B)=0.16。
抽一白球和抽一黑球的概率是0.24,两次皆是白球与两次黑球的概率是0.36和0.16。
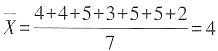 ,众数是指在次数分布中出现次数最多的那个数的数值,所以众数是5,中数是按顺序排列在一起的一组数据中居于中间位置的数,即2 3 4 4 5 5 5,所以中数是4。所以答案为B。
,众数是指在次数分布中出现次数最多的那个数的数值,所以众数是5,中数是按顺序排列在一起的一组数据中居于中间位置的数,即2 3 4 4 5 5 5,所以中数是4。所以答案为B。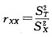 ;信度是被测团体真分数与实得分数的相关系数的平方,即
;信度是被测团体真分数与实得分数的相关系数的平方,即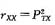 ;信度是一个测验与它的任意一个平行测验的相关系数,即rxx'=Pxx';信度的大小直接反映测验随机误差的大小。
;信度是一个测验与它的任意一个平行测验的相关系数,即rxx'=Pxx';信度的大小直接反映测验随机误差的大小。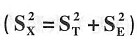 。
。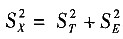 。根据CTT的数学模型及其假设,推导关系式(3.2)的过程如下:
。根据CTT的数学模型及其假设,推导关系式(3.2)的过程如下: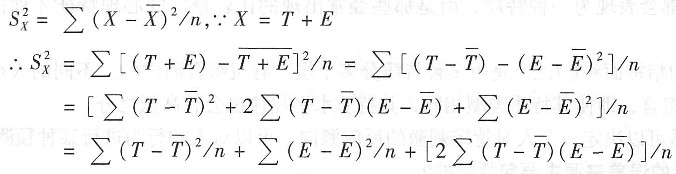
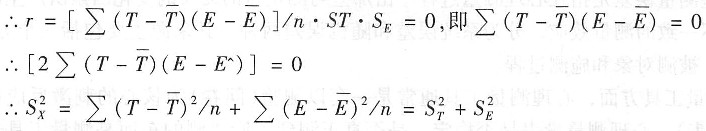
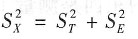
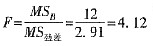 :
:
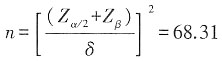
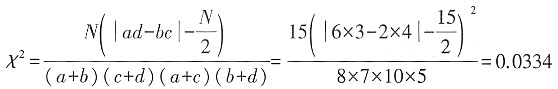
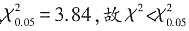 ,p>0.05
,p>0.05