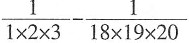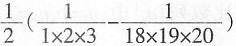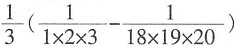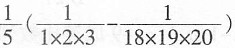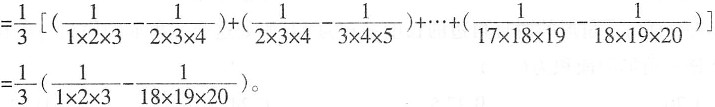数学计算从题后所给的四个选项中选出计算结果正确的一项。
4. 与385×
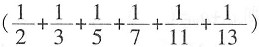
最接近的整数是______。
A B C D
B
[解析] 因为385=5×7×11,且
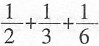
=1,所以
原式=385×

=385+7×11+5×11+5×7+385×
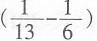
=518-
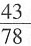
,注意到0.5<
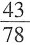
<1,所以与原式最接近的整数是517。
7. 设m,n是任意正数,且满足a·m
n+
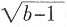
+(c-3)
2=0,则a,b,c之和为______。
A B C D
C
[解析] 对m、n取特殊值。取m=n=1,则a+
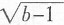
+(c-3)
2=0;取m=2,n=1,则2a+
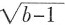
+(c-3)
2=0;联立以上两式,可得a=0,此时

+(c-3)
2=0,于是b=1,c=3,a,b,c之和为4。
10. 设a、b满足
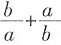
=2,则

=______。
A.
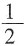
B.1
C.-1
D.
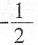
A B C D
A
[解析] 设a=b=1,代入代数式解得结果为
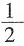
。
13. 设0<a<1,-1<6<-a,则下列代数式值最大的是______。
A.
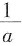
B.
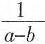
C.
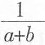
D.
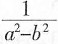
A B C D
A
[解析] 用特殊值法。取a=
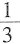
,b=
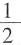
,则

=3,
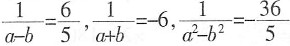
,最大的是3,所以选A。
17. 已知等差数列{a
n}前10项的和S
10=120,则a
1+a
10=______。
A B C D
[解析] 根据等差数列求和公式可得,S
10=
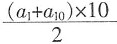
=120,因此a
1+a
10=24。
18. 已知等差数列{a
n}的公差为
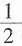
,且a
2+a
4…a
100=80,则
该数列前100项的和S
100=______。
A B C D
C
[解析] 由已知条件可得
a
2+a
4…+a
100=
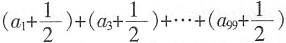
=80,因此a
1+a
3+…+a
99=80-
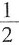
×50=55,故S
100=a
1+a
2+a
3+a
4+…+a
99+a
100=80+55=135。
21. 在等差数列{a
n}中,a
2=-6,a
8=6,若数列{a
n}的前n项和为S
n则______。
- A.S4<S5
- B.S4=S5
- C.S6<S5
- D.S6=S5
A B C D
B
[解析] 由已知可得公差d=
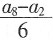
=2,再由a
2=-6可得a
5=0,故S
4=S
5。
23. 若干人围成8圈,一圈套一圈,从外向内各圈人数依次少4人。如果最内圈有32人,共有______。
A B C D
B
[解析] 依题意,从内向外,各圈人数依次增加4人,则每圈人数可看成首项为a
1=32,公差d=4,项数n=8的等差数列,求总人数
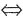
等差数列求和。直接代入求和公式S
n=na
1+
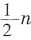
(n-1)d,可得人数为32×8+
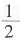
×8×(8-1)×4=368人,选B。
24. {a
n}是一个等差数列,a
3+a
n=8,a
11-a
4=4,则数列前13项之和是______。
A B C D
C
[解析] 由对称公式可知a3+a11=a4+a10,题干两式相加得(a3+a11)+a7
-(a4+a10)=12,因此a7=12。数列前13项的中项恰好为a7。
由中项求和公式可知,数列前13项的和S13=13a7=13×12=156,选C。
27. 等差数列{a
n}中a
1+a
2+a
3=-24,a
18+a
19+a
20=78,则此数列前20项
的和等于______。
A B C D
B
[解析] 等差数列求和。由已知可得(a
1+a
2+a
3)+(a
18+a
19+a
20)=-24+78=54,由对称公式,a
1+a
20=a
2+a
19=a
3+a
18,则(a
1+a
20)+(a
2+a
19)+(a
3+a
18)=54,3×(a
1+a
20)=54,即a
1+a
20=18,所以S
20=
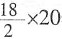
=180。
32. 在等比数列{a
n}中,a
1=1,a
10=3,则a
1a
2a
3a
4a
5a
6a
7a
8a
9=______。
A.81
B.27
C.
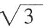
D.243
A B C D
A
[解析] 根据等比数列的性质可得,a2a9=a3a8=a4a7=a5a6=a1a10=3,所以
a2a3a4a5a6a7a8a9=(a2a9)(a3a8)(a4a7)(a5a6)=34=81。
34. 等比数列{a
n}中,a
6+a
2=34,a
6-a
2=30,那么a
4=______。
A B C D
A
[解析] 由a
6+a
2=34,a
6-a
2=30,解得a
6=32,a
2=2。根据等比数列的性
质可得,
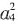
=a
2a
6=64,且a
4与a
2同号,故a
4=8。
35. 在等比数列{a
n}中,a
n>0且a
2=1-a
1,a
4=9-a
3,则a
4+a
5值为______。
A B C D
B
[解析] 此题属于等比数列问题。根据a
m=a
1q
n-1,可得
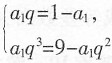
,化简得q=±3,由于该数列是正项数列,所以舍去负值,即q=3。
则a
4+a
5=q(a
3+a
4)=3×9=27。
36. 某人在保险柜中存放了M元现金,第一天取出它的

,以后每天取出前一天所取的

,共取了7次,保险柜中剩余的现金为______。
A.
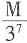
元
B.
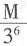
元
C.
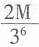
元
D.
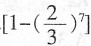
M元
A B C D
A
[解析] 每天取钱数是一个首项为
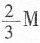
,公比为

的等比数列,
连续取7天共取S
7=
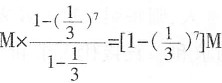
元。剩余现金为M-
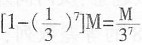
元,选A。
39.
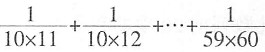
=______。
A.
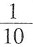
B.
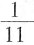
C.
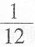
D.
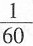
A B C D
C
[解析] 裂项求和。
原式=
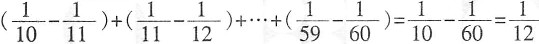
。
40.
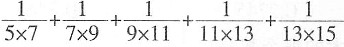
=______。
A.

B.
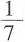
C.
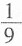
D.
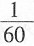
A B C D
D
[解析] 原式
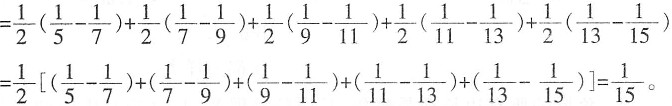
41.
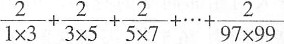
=______。
A.
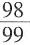
B.
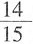
C.
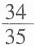
D.
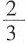
A B C D
A
[解析] 原式
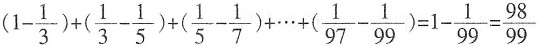
。
42.
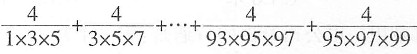
=______。
A.
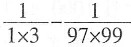
B.
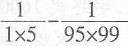
C.
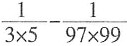
D.

A B C D
A
[解析] 原式
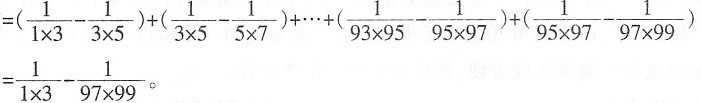
43.

=______。
A.
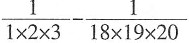
B.
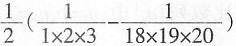
C.
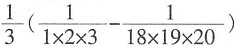
D.
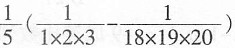
A B C D
C
[解析] 原式
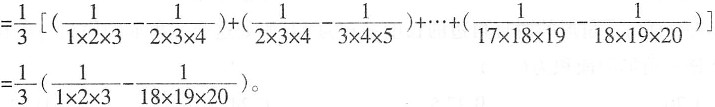
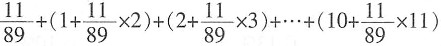 的数点后前四位是______。
的数点后前四位是______。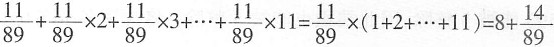 的小数部分相同,故只需考虑
的小数部分相同,故只需考虑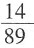 的小数即可。因为
的小数即可。因为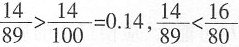 =0.2,四个选项中只有B项符合。
=0.2,四个选项中只有B项符合。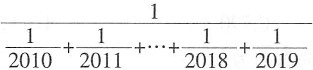 的整数部分是______。
的整数部分是______。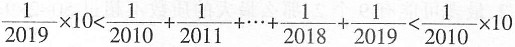 ,所以201.0<N<201.9,则N的整数部分是201。
,所以201.0<N<201.9,则N的整数部分是201。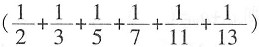 最接近的整数是______。
最接近的整数是______。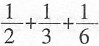 =1,所以
=1,所以
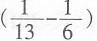
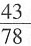 ,注意到0.5<
,注意到0.5<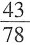 <1,所以与原式最接近的整数是517。
<1,所以与原式最接近的整数是517。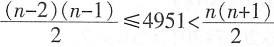 ,即(n-2)(n-1)≤9902<n(n+1)。因为98×99<99×100<9902<100×101,所以n=100。缺失的那张页码之和为
,即(n-2)(n-1)≤9902<n(n+1)。因为98×99<99×100<9902<100×101,所以n=100。缺失的那张页码之和为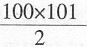 -4951=99,所以奇数页码是49。
-4951=99,所以奇数页码是49。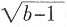 +(c-3)2=0,则a,b,c之和为______。
+(c-3)2=0,则a,b,c之和为______。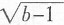 +(c-3)2=0;取m=2,n=1,则2a+
+(c-3)2=0;取m=2,n=1,则2a+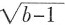 +(c-3)2=0;联立以上两式,可得a=0,此时
+(c-3)2=0;联立以上两式,可得a=0,此时 +(c-3)2=0,于是b=1,c=3,a,b,c之和为4。
+(c-3)2=0,于是b=1,c=3,a,b,c之和为4。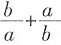 =2,则
=2,则 =______。
=______。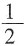
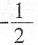
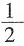 。
。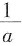
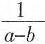
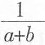
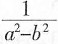
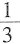 ,b=
,b=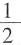 ,则
,则 =3,
=3,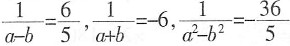 ,最大的是3,所以选A。
,最大的是3,所以选A。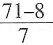 +1=10项,根据等差数列的求和公式可得,S=
+1=10项,根据等差数列的求和公式可得,S=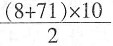 =395。
=395。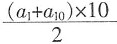 =120,因此a1+a10=24。
=120,因此a1+a10=24。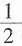 ,且a2+a4…a100=80,则
,且a2+a4…a100=80,则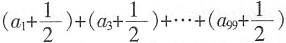 =80,因此a1+a3+…+a99=80-
=80,因此a1+a3+…+a99=80-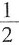 ×50=55,故S100=a1+a2+a3+a4+…+a99+a100=80+55=135。
×50=55,故S100=a1+a2+a3+a4+…+a99+a100=80+55=135。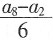 =2,再由a2=-6可得a5=0,故S4=S5。
=2,再由a2=-6可得a5=0,故S4=S5。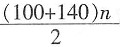 =180·(n-2),解得n=6。故这个凸多边形的边数为6。
=180·(n-2),解得n=6。故这个凸多边形的边数为6。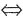 等差数列求和。直接代入求和公式Sn=na1+
等差数列求和。直接代入求和公式Sn=na1+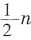 (n-1)d,可得人数为32×8+
(n-1)d,可得人数为32×8+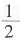 ×8×(8-1)×4=368人,选B。
×8×(8-1)×4=368人,选B。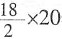 =180。
=180。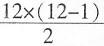 ×100=18600元。因此仅从经济收入方面考虑,去乙公司合算。
×100=18600元。因此仅从经济收入方面考虑,去乙公司合算。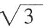
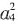 =a2a6=64,且a4与a2同号,故a4=8。
=a2a6=64,且a4与a2同号,故a4=8。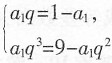 ,化简得q=±3,由于该数列是正项数列,所以舍去负值,即q=3。
,化简得q=±3,由于该数列是正项数列,所以舍去负值,即q=3。 ,以后每天取出前一天所取的
,以后每天取出前一天所取的 ,共取了7次,保险柜中剩余的现金为______。
,共取了7次,保险柜中剩余的现金为______。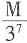 元
元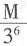 元
元 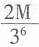 元
元 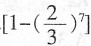 M元
M元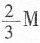 ,公比为
,公比为 的等比数列,
的等比数列,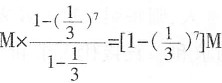 元。剩余现金为M-
元。剩余现金为M-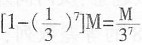 元,选A。
元,选A。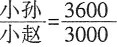 =1.2,则小周是小孙的1.2倍,比小孙多(1.2-1)×3600=720元。
=1.2,则小周是小孙的1.2倍,比小孙多(1.2-1)×3600=720元。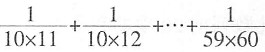 =______。
=______。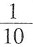
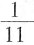
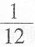
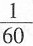
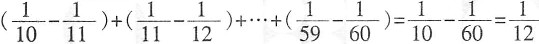 。
。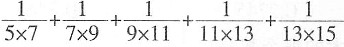 =______。
=______。
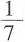
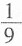
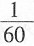
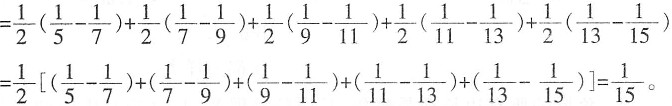
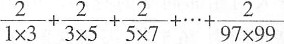 =______。
=______。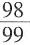
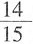
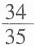
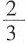
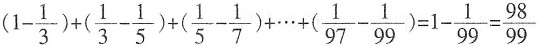 。
。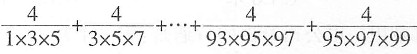 =______。
=______。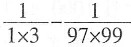
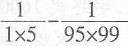
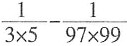

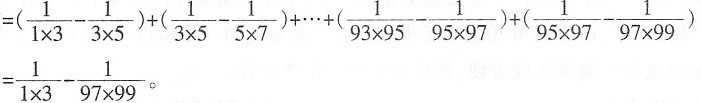
 =______。
=______。