银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
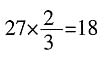 次;李四所属部门共锯了28段,能被4整除,故属于甲部门,共锯了
次;李四所属部门共锯了28段,能被4整除,故属于甲部门,共锯了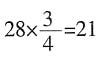 次;王五所属部门共锯了34段,属于丙部门,共锯了
次;王五所属部门共锯了34段,属于丙部门,共锯了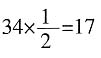 次。相同时间丙部门所锯次数最少,即速度最慢,选择B。
次。相同时间丙部门所锯次数最少,即速度最慢,选择B。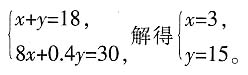
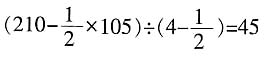 人,乙组人数为105-45=60人。
人,乙组人数为105-45=60人。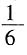 的营养。那么,由割下来的草所制成的干草可供多少头牛吃20天?______
的营养。那么,由割下来的草所制成的干草可供多少头牛吃20天?______ 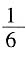 ,则只有500份草的营养,可供500÷20=25头牛吃20天。
,则只有500份草的营养,可供500÷20=25头牛吃20天。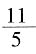 头牛吃10天,2头牛吃14天,则可供
头牛吃10天,2头牛吃14天,则可供 头牛吃多少天?”
头牛吃多少天?”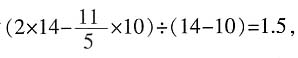 原有的草量为(2-1.5)×14=7,所以可供
原有的草量为(2-1.5)×14=7,所以可供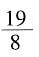 头牛吃
头牛吃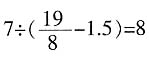 天。
天。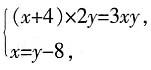 解得
解得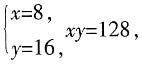 选B。
选B。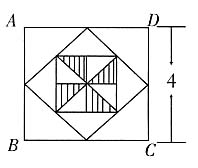
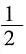 ,小正方形是中间正方形面积的
,小正方形是中间正方形面积的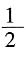 。所以阴影面积
。所以阴影面积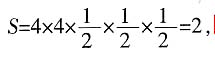 选B。
选B。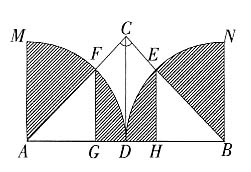
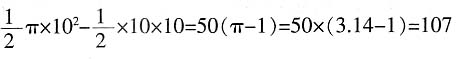 平方厘米。所以选C。
平方厘米。所以选C。
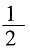

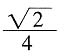
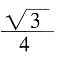
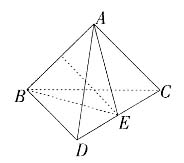
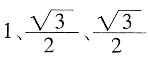 的等腰三角形,底边的高为
的等腰三角形,底边的高为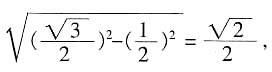 面积是
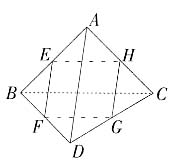
面积是 图2中切面EFGH是边长为
图2中切面EFGH是边长为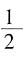 的菱形,根据正四面体的对称性可知,其对角线EG和FH相等,故EFGH是正方形,面积是
的菱形,根据正四面体的对称性可知,其对角线EG和FH相等,故EFGH是正方形,面积是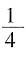 。
。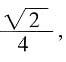 选择C。
选择C。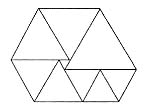


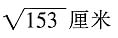
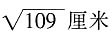


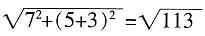 厘米。
厘米。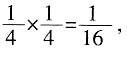 与水直接接触的总面积为原来立方体的64×
与水直接接触的总面积为原来立方体的64×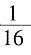 =4倍,即3.4×4=13.6平方米。
=4倍,即3.4×4=13.6平方米。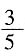 的容器用时18分钟,那么可知灌满
的容器用时18分钟,那么可知灌满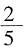 的容器需要用时12分钟。但实际上这部分只用了3分钟,因此铁块的体积是
的容器需要用时12分钟。但实际上这部分只用了3分钟,因此铁块的体积是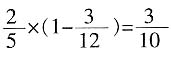 的容器容积。设容器容积为1,设铁块底面积为S1,容器底面积为S2。则S1×20cm=
的容器容积。设容器容积为1,设铁块底面积为S1,容器底面积为S2。则S1×20cm=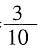 ,S2×50cm=1,得到S1:S2=3:4。
,S2×50cm=1,得到S1:S2=3:4。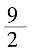
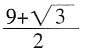
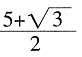
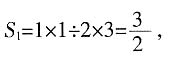 增加的表面积
增加的表面积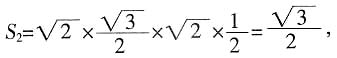 故剩下的面积
故剩下的面积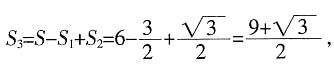 选C。
选C。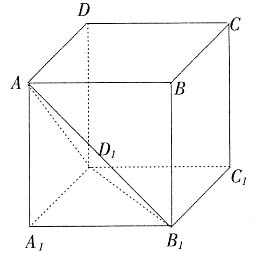
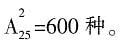
 种方法;再挑选蔬菜,有
种方法;再挑选蔬菜,有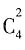 种方法;最后挑选点心,有
种方法;最后挑选点心,有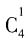 种方法。由于挑选的过程是分步进行的,因此应该用乘法原理,可以有
种方法。由于挑选的过程是分步进行的,因此应该用乘法原理,可以有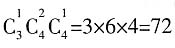 种方法。
种方法。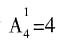 种;两盏时为
种;两盏时为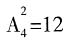 种;三盏时为
种;三盏时为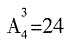 种;四盏时为
种;四盏时为 种。共有4+12+24+24=64种。
种。共有4+12+24+24=64种。