计算题1. 已知梁的弯矩图如图所示。试作梁的载荷图和剪力图。
解:所有节点按图所示标记。
(a)①绘制剪力图
AC段弯矩图为斜率为正的直线,由弯矩、剪力之间的微分关系可知,该段剪力图为水平直线,且为正值,为1kN;同理CD段也为水平直线,且为负值,为

DB段剪力为零。
②绘制载荷图
由剪力图可知,在A截面有向上集中力F
A=1kN,C截面有向下集中力F
C=2kN,D截面有向上集中力F
D=1kN。
由弯矩图中弯矩的突变值可知,在D截面有顺时针的集中力偶M
D=3kN·m;B截面有逆时针的集中力偶M
B=1kN·m。
③绘制剪力图和载荷图,如图(a)所示。
(b)①绘制剪力图
AB段弯矩图为斜率为负的直线,由弯矩、剪力之间的微分关系可知,该段剪力图为水平直线,且为负值,为1kN。
②绘制载荷图
由剪力图可知,在A截面有向下集中力F
A=1kN,B截面有向上集中力F
B=1kN。
由弯矩图中弯矩的突变值可知,在C截面有顺时针的集中力偶M
C=3kN·m;D截面有顺时针的集中力偶M
D=3kN·m。
③绘制剪力图和载荷图,如图(b)所示。
(c)①绘制剪力图
AC段弯矩图为零,由弯矩、剪力之间的微分关系可知,该段剪力也为零;同理CD段为水平直线,且为正值,为10kN;DB段剪力为零。
②绘制载荷图
由剪力图可知,在C截面有向上集中力F
C=10kN,D截面有向下集中力F
D=10kN。
由弯矩图中弯矩的突变值可知,在D截面有逆时针的集中力偶M
D=20kN·m。
③绘制剪力图和载荷图,如图(c)所示。
(d)①绘制剪力图
AC段弯矩图为水平直线,由弯矩、剪力之间的微分关系可知,该段剪力为零;同理CD剪力图段为水平直线,且为负值,为

DB段剪力图段为水平直线,且为正值,为3kN。
②绘制载荷图
由剪力图可知,C截面有向下集中力F
C=2kN;D截面有向上集中力F
D=5kN;B截面有向下集中力F
B=3kN。
由弯矩图中弯矩的突变值可知,在A截面有顺时针的集中力偶M
A=1kN·m。
③绘制剪力图和载荷图,如图(d)所示。
2. 在图1所示平面桁架中,所有杆件的E皆相同,CA,AB,BF三杆的横截面面积为30cm
2,其余各杆的截面面积均为15cm
2。a=6m,F=120kN。试求AB杆的轴力。
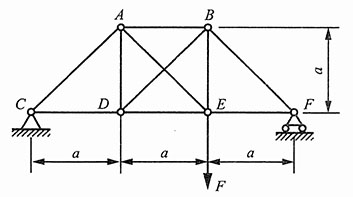
图1
解:将AB杆截开,代之以反力X
1,并对各杆进行编号,其相当系统如图2所示,则力法方程:δ
11X
1+Δ
1F=0。
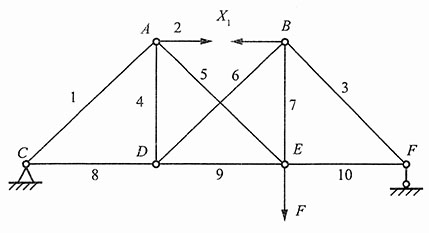
图2
首先在相当系统上只作用力F,并求出此时各杆内力F
Ni;其次在相当系统上只作用单位力,即令X
1=1,求得此时各杆内力
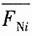
。结果如下表所示。
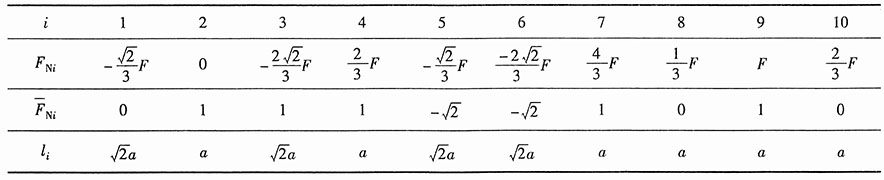
由莫尔定理可得:
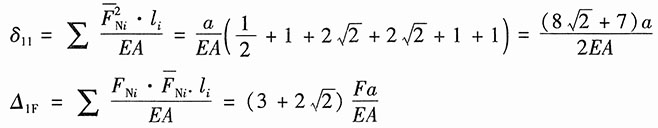
将以上各式代入力法方程,可得:
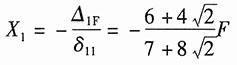
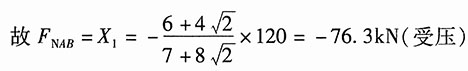
3. 为改善桥式起重机大梁的刚度和强度,在大梁的下方增加预应力拉杆CD。梁的计算简图如图1(b)所示。由于CC'和DD'两杆甚短,且刚度较大,其变形可以不计。试求拉杆CD因吊重P而增加的内力。

图1
解:将CD截开,代之以反力X
1,其相当系统如图2(a)所示,则正则方程:
δ
11X
1+Δ
1P=0。
设梁与拉杆的材料相同,即弹性模量均为E,记二者横截面面积分别为A和A
1。
首先作梁在外载荷P单独作用下的弯矩图,如图2(b)所示;其次作梁和拉杆在单位力作用下的弯矩和轴力图,分别如图2(c)所示。
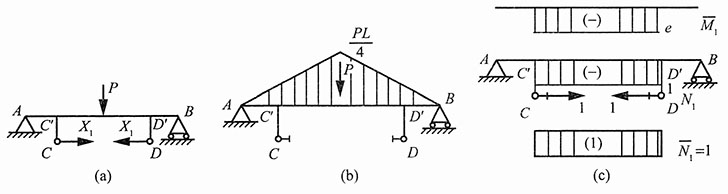
图2
则有:
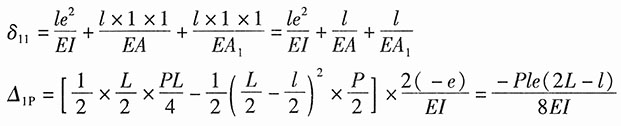
代入正则方程,可得:

即为拉杆增加的内力。
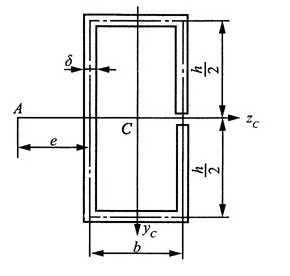
4. 试确定下图所示箱形开口截面的弯曲中心A的位置。设截面的壁厚δ为常量。且壁厚及开口切缝都很小。
解:如图所示,截面对z轴的惯性矩:
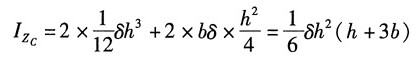
BF段:上半部分面积对z轴的静矩
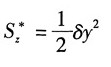
则该段任意截面上的切应力:
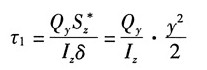
BD段:左半部分面积对z轴的静矩
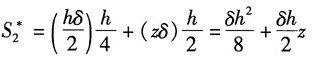
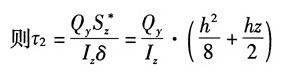
同理,BE段:

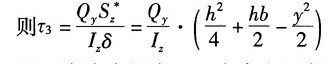
以C点为力矩中心,由合力矩定理可得:
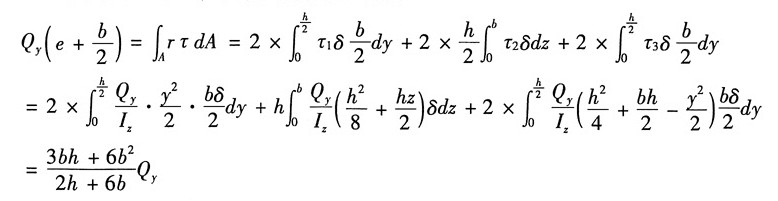
解得:
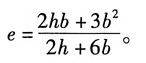
5. 在如图1所示结构中,杆件①由钢制成,A
1=20cm
2,E
1=200GPa,杆件②由铜制成,A
2=10cm
2,E
2=100GPa。若AB杆可视为刚体,试求节点位移和①,②两杆的应力。
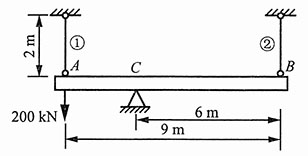
图1
解:如图2所示,节点1、4为固定铰,而AB杆为刚性杆,故可得:u
1=u
4=0,u
3=-2u
2。
钢杆①的单元刚度方程为:
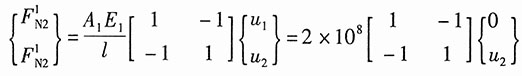
铜杆②的单元刚度方程为:
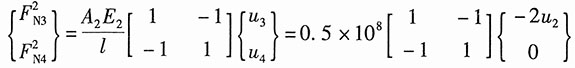
AB杆的平衡方程:
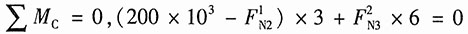
将单元刚度方程中的
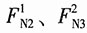
代入以上方程,得:
(200×10
3-2×10
8u
2)×3+(-10
8u
2)×6=0
解得:u
2=0.5×10
-3m
故u
3=-2u
2=-1×10
-3m
各杆轴力:
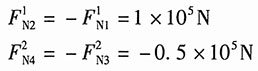
故各杆应力:
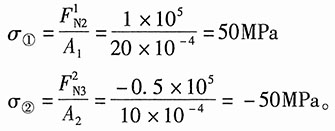
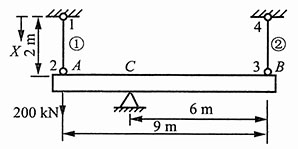
图2
6. 如图所示AB轴的转速n=120r/min,从B轮输入功率P=44.13kW,功率的一半通过锥形齿轮传给垂直轴Ⅱ,另一半由水平轴Ⅰ输出。已知D
1=600mm,D
2=240mm,d
1=100mm,d
2=80mm,d
3=60mm,[τ]=20MPa。试对各轴进行强度校核。
解:(1)校核水平轴I轴
Ⅰ轴传递的功率:

则其传递的扭矩:

该轴上的最大切应力为

故Ⅰ轴的强度满足要求,是安全的。
(2)校核垂直轴Ⅱ轴
Ⅱ轴传递的功率:

转速:

则其传递的扭矩:

该轴上的最大切应力为

故Ⅱ轴的强度满足要求,是安全的。
(3)校核AB轴
AB轴传递的扭矩:

则轴上的最大切应力为

故该轴强度满足要求。
7. 炮筒横截面如图所示。在危险点处。σ
t=550MPa,σ
r=-350MPa,第三个主应力是垂直于图面是拉应力。且其为420MPa。试按第三和第四强度理论。计算其相当应力。
解:根据题意,主应力为:
σ
1=σ
t=550MPa,σ
2=σ
z=420MPa,σ
3=σ
r=-350MPa
由第三强度理论可得:σ
r3=σ
1-σ
3=(550+350)MPa=900MPa
由第四强度理论可得:
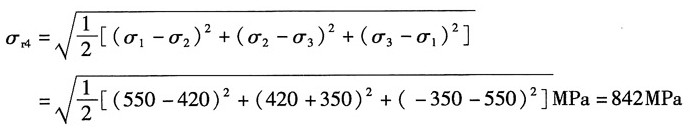
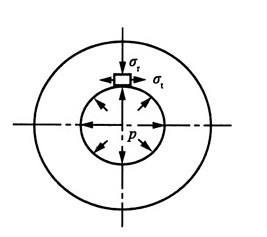
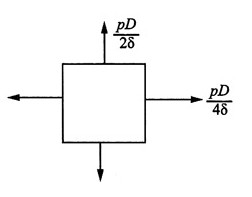
8. 钢制圆柱形薄壁容器。直径为800mm,壁厚δ=5mm,[σ]=120MPa。试用强度理论确定可能承受的内压强p。
解:如图所示,为该薄壁容器危险点的应力状态。
该点的主应力为:
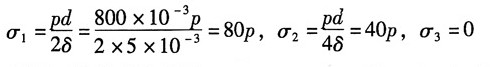
按第三强度理论校核:σ
r3=σ
1-σ
3=80p-0≤[σ]
可得:
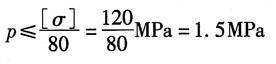
按第四强度理论校核:
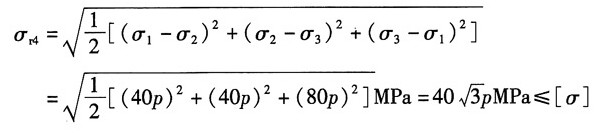
可得:
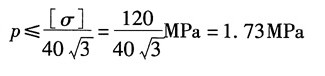
9. 如坐标系取y轴向下为正(如图所示),试证明挠曲线的微分方程式
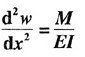
应改为
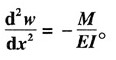
证:根据数学计算公式可知:
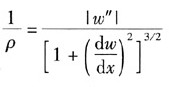
在小变形情况下,有
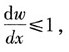
因此近似有
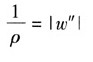
又
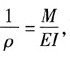
可得:

对于图中所示坐标有M>0,则
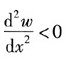
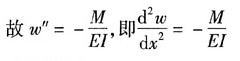
命题得证。
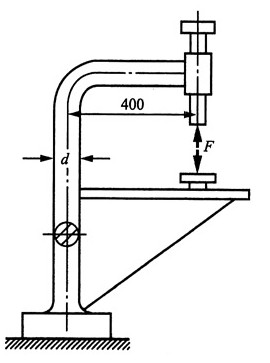
10. 如图所示钻床的立柱为铸铁制成,F=18kN,许用拉应力[σ
t]=35MPa。试确定立柱所需直径d。
解:立柱截面上的内力:
F
N=F=18kN,M=0.4F=7.2 kN·m
截面内侧有最大拉应力:

由强度条件σ
max≤[σ
t]得:
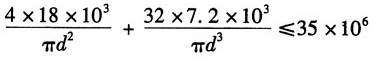
解得立柱所需直径:d≥128mm。
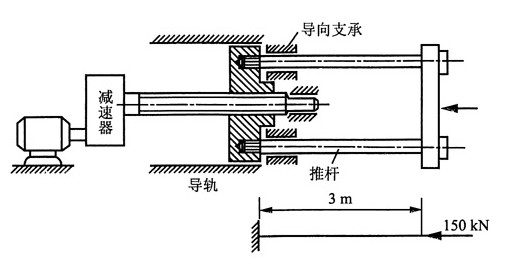
11. 某轧钢车间使用的螺旋推钢机的示意图如图所示。推杆由丝杆通过螺母来带动。已知推杆横截面的直径d=12.5cm,材料为Q255钢。当推杆全部推出时,前端可能有微小的侧移,故简化为一端固定、一端自由的压杆。这时推杆的伸出长度为最大值。l
max=3m。取稳定安全因数n
st=4。试校核压杆的稳定性。
解:对于Q255钢,E=210GPa,σ
p=240MPa,则有:
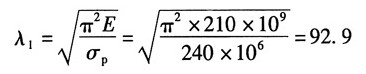
根据题意,推杆长度系数μ=2,则其柔度:
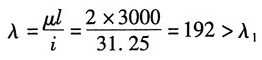
由此可知其为大柔度杆,故由欧拉公式计算其临界压力:
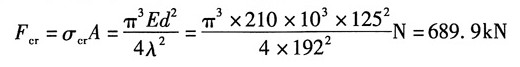
安全因数:
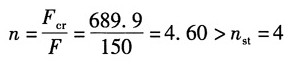
杆的稳定性满足要求。
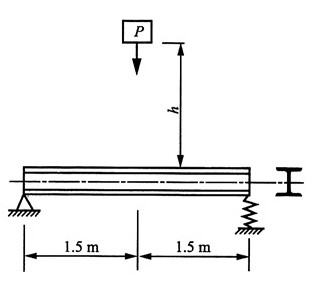
12. 如图所示16号工字钢左端铰支,右端置于螺旋弹簧上。弹簧共有10圈,其平均直径D=10cm。簧丝的直径d=20mm。梁的许用应力[σ]=160MPa,弹性模量E=200GPa;弹簧的许用切应力[τ]=200MPa,切变模量G=80GPa。今有重量P=2kN的重物从梁的跨度中点上方自由落下,试求其许可高度h。
解:查型钢表16号工字钢:I=1130cm
4,W=141cm
3 P以静荷载作用于梁上时,作用点梁中点处的位移由两部分组成:
弹簧变形量:
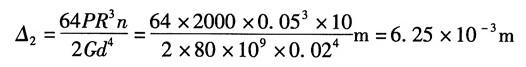
P作用下挠度:
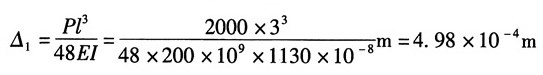
故梁中点处静位移:
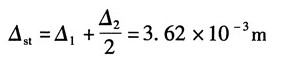
则动荷系数:
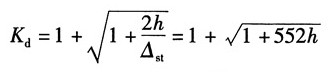
跨中截面上有最大静应力:
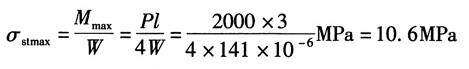
①根据梁的强度条件:σ
dmax=K
dσ
stmax≤[σ]
将动荷因数K
d代入上式并整理,解得:h≤0.358m。
②对于弹簧来说
根据强度条件:
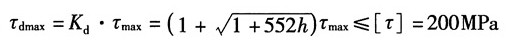
由
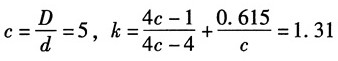
得,静载时最大切应力:
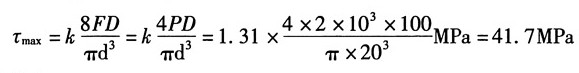
代入强度条件得h≤24.3mm
综上,许可高度:[h]=24.3mm。
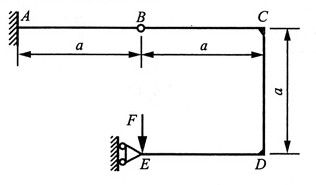
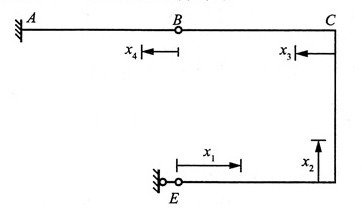
13. 刚架BCDE用铰与悬臂梁的自由端B相连接,两者的EI相同,且等于常量。若不计结构的自重,试求F力作用点E的铅垂位移。
解:用能量法求解,建立如图所示坐标系。
列出各段弯矩方程及其对力F的偏导:
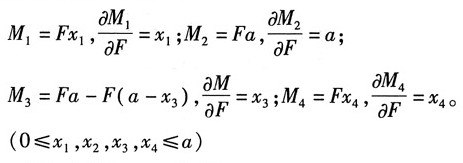
由卡氏定理得:
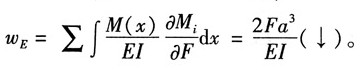
14. 写出图1所示刚架的整体刚度方程。设刚架各杆的EI和EA皆相等,且E=200GPa,A=30×10
-4m
2,I=2400×10
-8m
4。
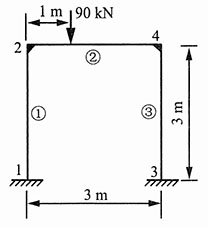
图1
解:首先将作用在单元②上的中间载荷等效为作用在节点2、4上的载荷,得到如图2所示的杆系。

图2
对于①、②、③单元均有:
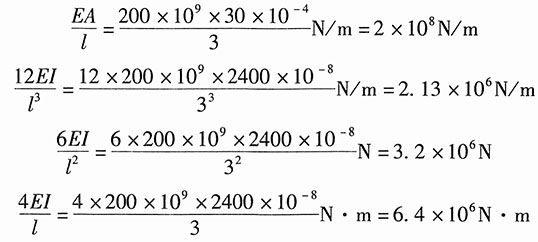
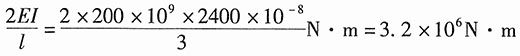
代入公式得单元①、单元②、单元③的单元刚度矩阵均为:

经坐标变换,把以上单元刚度矩阵转变为整体坐标中的单元刚度矩阵。
单元①、③:θ=90°,cosθ=0,sinθ=1,可得坐标变换矩阵为:

则根据公式可求得单元①在整体坐标中的单元刚度矩阵:
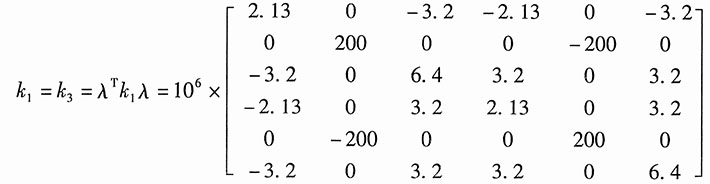
单元②:θ=0°,即有
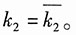
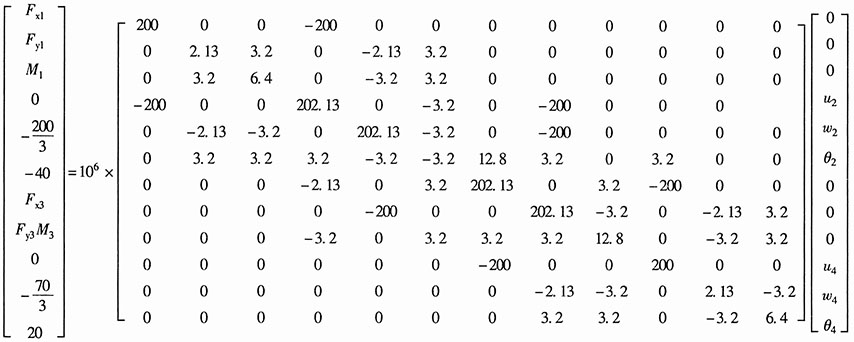
将以上得到的单元刚度矩阵叠加,得到整体刚度方程:
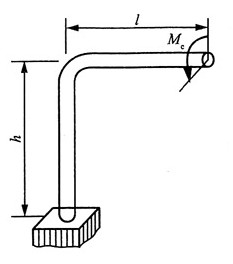
15. 如图所示折杆的横截面为圆形。在力偶矩M
e作用下,试求折杆自由端的线位移和角位移。
解:自由端的水平线位移是由大小为M
e的力偶矩作用于竖直部分顶端弯曲变形引起的,因此与竖直部分的顶端的线位移相同,则自由端水平位移:

自由端的转角由水平部分的扭转角位移与竖直部分顶端弯曲变形叠加而得,则自由端转角:
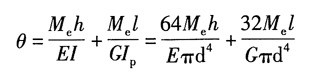
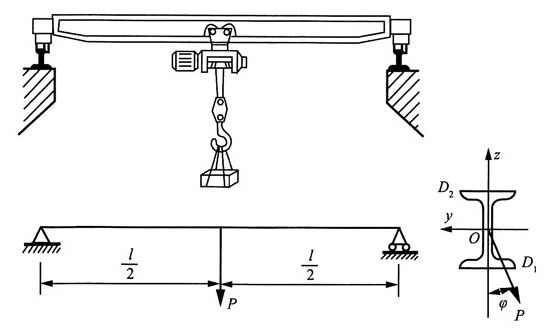
16. 桥式起重机大梁为32a工字钢,[σ]=160MPa,l=4m。行进时由于某种原因,载荷P偏离纵向对称面一个角度φ。若φ=15°,P=30kN,试校核梁的强度,并与φ=0的情况相比较。
解:由图可得,P
z=Pcosφ,P
y=Psinφ。
分析可知,梁的危险截面为梁的中点处截面,且最危险点为D
1点(受拉)和D
2点(受压)。
最大弯曲正应力为:
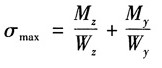
其中
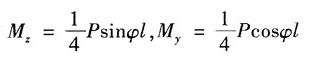
查型钢表得32a工字钢截面性质:W
y=692cm
3,W
z=70.8cm
3 当φ=15°时,
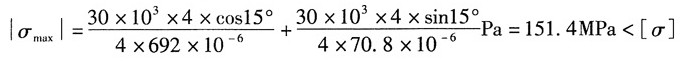
故此时梁强度满足要求。
当φ=0°时,最大正应力:
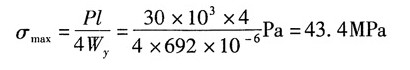
比较可得:
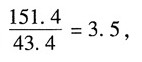
即载荷偏离纵向对称面15°时比不偏离时最大应力增长了3.5倍。
17. 如图所示飞轮的最大圆周速度v=30m/s,材料单位体积的质量为7.41×10
3kg/m
3。若不计轮幅的影响,试求轮缘内的最大正应力。
解:假想沿过直径的面将圆环断开,则由平衡条件得:
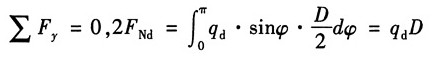
其中,沿轴线均匀分布的惯性力集度:
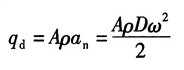
则有:
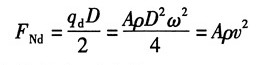
轮缘内的最大正应力:
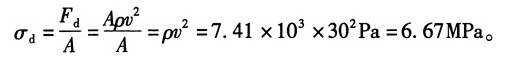
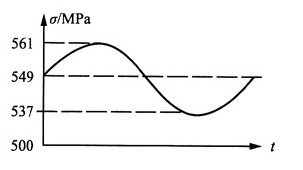
18. 柴油发动机连杆大头螺钉在工作时受到最大拉力F
max=58.3kN,最小拉力F
min=55.8kN。螺纹处内径d=11.5mm。试求其平均应力σ
m,应力幅σ
a,循环特征r,并作出σ-t曲线。
解:根据题意,最大应力:
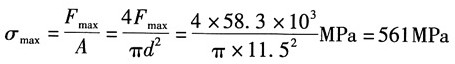
最小应力:
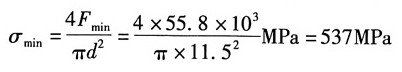
则平均应力:
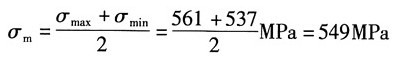
应力幅:
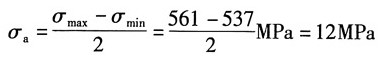
循环特征:
σ-t曲线如图所示。
19. 作下图1所示刚架的弯矩图。设刚架各杆的EI皆相等。
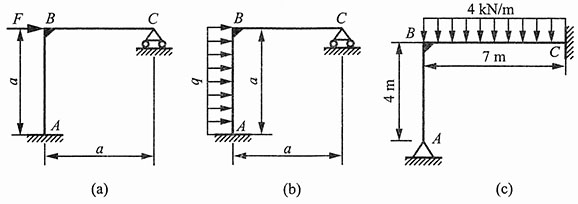
图1
解:(1)如图2(a)所示,解除支座C多余约束,代之以支反力X
1,其相当系统如图2(a)所示。则力法方程:δ
11X
1+Δ
1F=0。
分别作梁在已知载荷F和单位力作用下的弯矩图,如图2(a
1)、(a
2)所示。由图乘法可得:
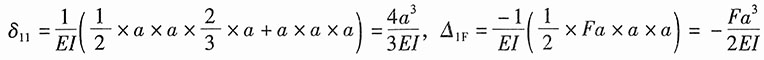
将以上结果代入力法方程,可得:
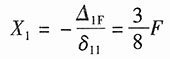
由此可绘制刚架弯矩图,如图2(a
3)所示。
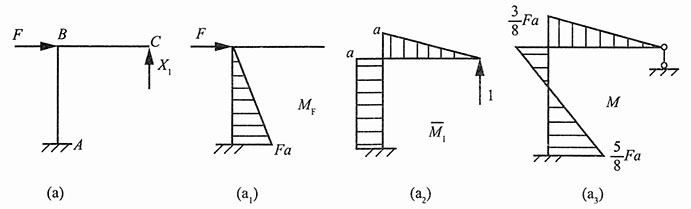
图2
(2)如图3(b)所示,解除支座C端多余约束,代以反力X
1,其相当系统如图3(b)所示。则力法方程:δ
11X
1+Δ
1F=0。
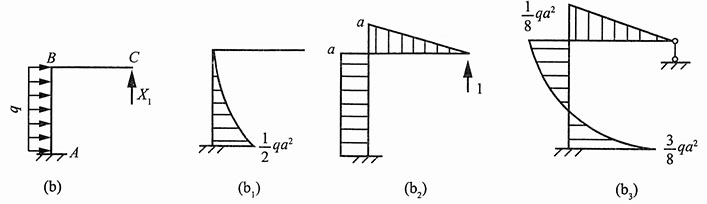
图3
分别作出梁在已知均布载荷q和单位力作用下的弯矩图,如图3(b
1)、(b
2)所示,
由图乘法可得:
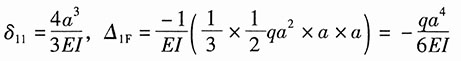
将以上各式代入力法方程,解得:
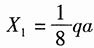
由此可绘制刚架弯矩图,如图2(b
3)所示。
(2)如图4(c)所示,解除铰支座A约束,代之以反力X
1,X
2,其相当系统如图4(c)所示,则力法方程为:
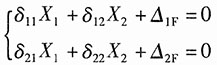
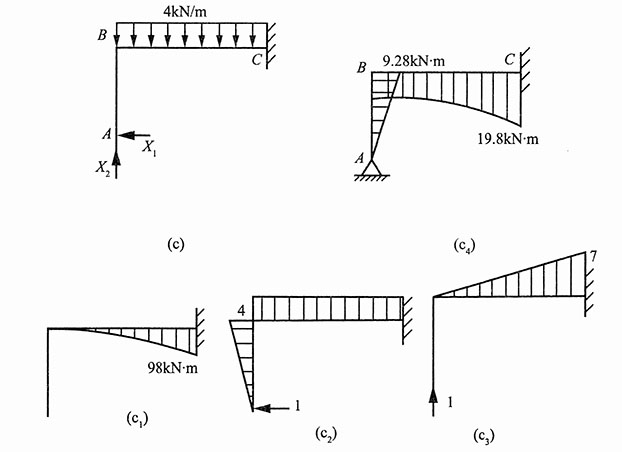
图4
分别作梁在已知均布载荷q和单位力作用下的弯矩图,如图4(c
1)、(c
2)、(c
3)所示,由图乘法可得:
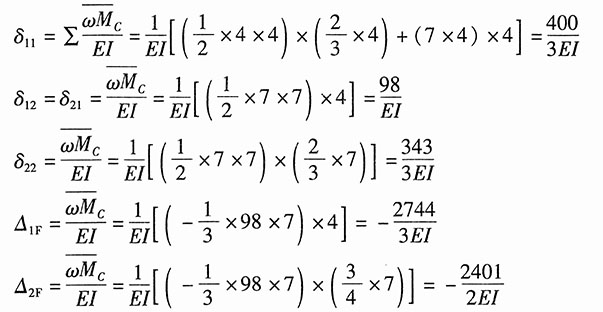
将以上各式代入力法方程,可得:X
1=-2.32kN,X
2=12.5kN。
由此可绘制刚架弯矩图,如图4(c
4)所示。
20. 作图所示刚架的弯矩图。
解:(a)对刚架进行受力分析,由平衡条件可得各支座反力。

BC段为一斜直线,且B截面的弯矩值:

由于AB段集中载荷的作用,该段弯矩图为抛物线,且绘制弯矩图时,将弯矩画在刚架受压一侧,如图(a)所示。
(b)根据图中已知条件绘制弯矩图,将弯矩画在刚架受压一侧,如图(b)所示。
(c)对刚架进行受力分析,由平衡条件可得各支座反力:
F
RAs=3kN(←),F
RAy=3kN(↑),F
RD=5kN(↑)
绘制弯矩图时,将弯矩画在剐架受压一侧,如图(c)所示。
(d)对刚架进行受力分析,由平衡条件可得各支座反力:

绘制弯矩图时,将弯矩画在刚架受压一侧,如图(d)所示。



 DB段剪力为零。
DB段剪力为零。 DB段剪力图段为水平直线,且为正值,为3kN。
DB段剪力图段为水平直线,且为正值,为3kN。

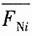 。结果如下表所示。
。结果如下表所示。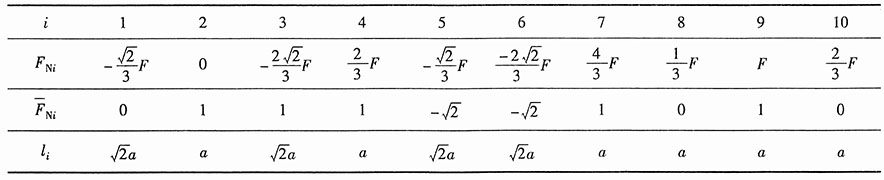
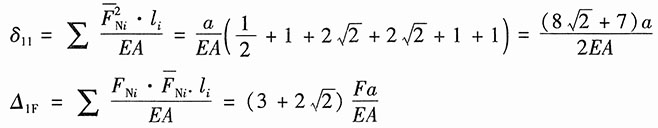
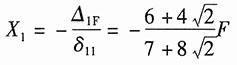
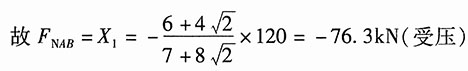


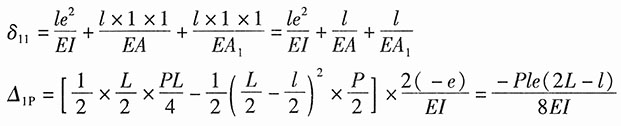


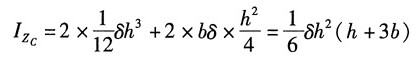
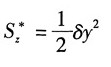
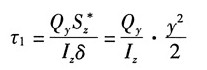
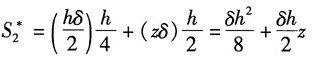
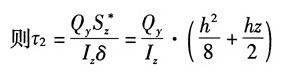

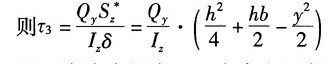
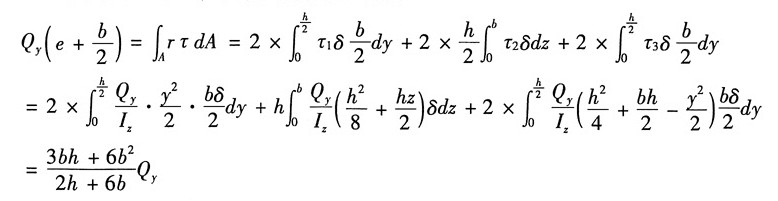
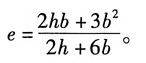

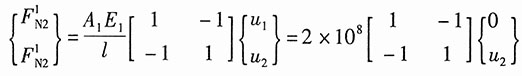
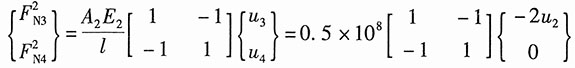
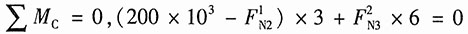
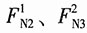 代入以上方程,得:
代入以上方程,得: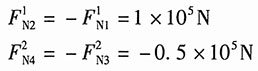
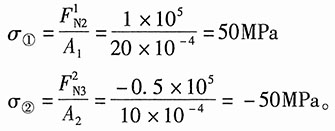











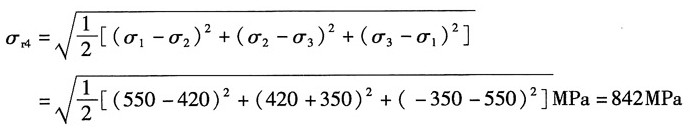
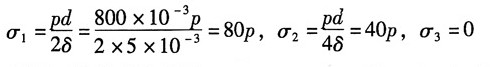
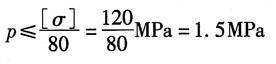
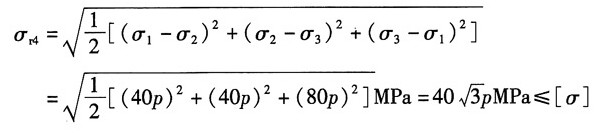
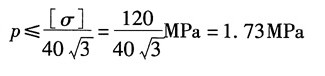
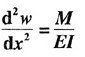 应改为
应改为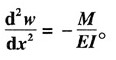
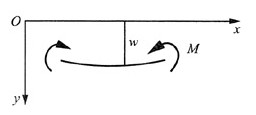
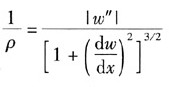
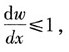 因此近似有
因此近似有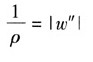
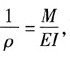 可得:
可得:
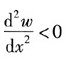
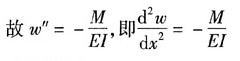

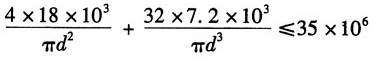
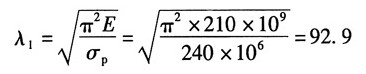
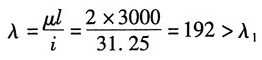
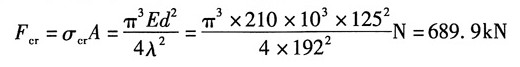
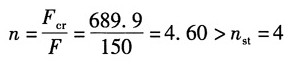
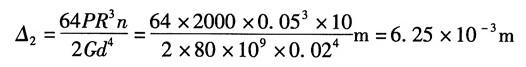
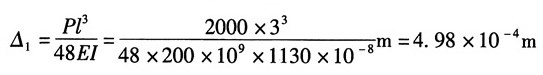
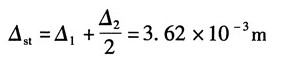
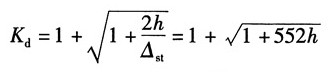
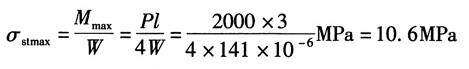
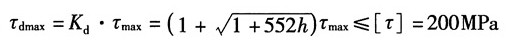
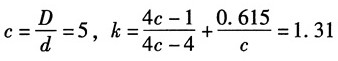 得,静载时最大切应力:
得,静载时最大切应力: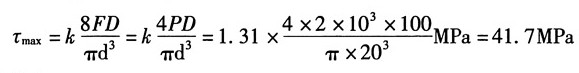
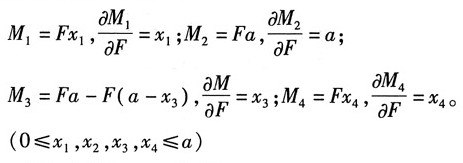
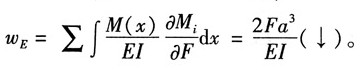


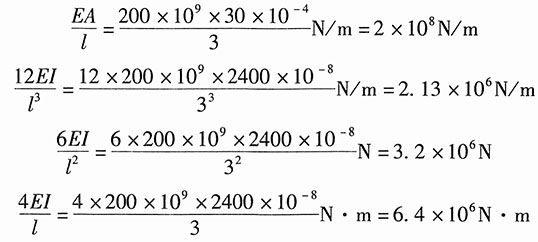
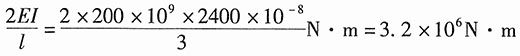



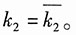


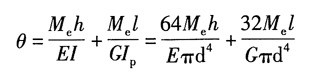
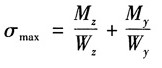
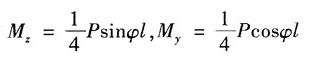
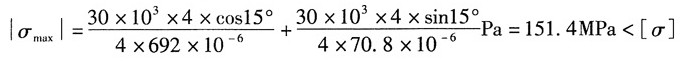
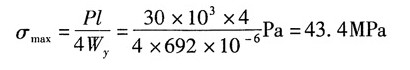
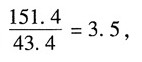 即载荷偏离纵向对称面15°时比不偏离时最大应力增长了3.5倍。
即载荷偏离纵向对称面15°时比不偏离时最大应力增长了3.5倍。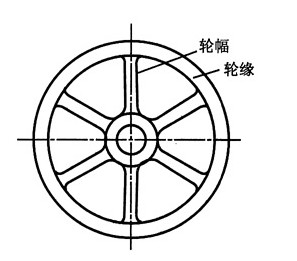
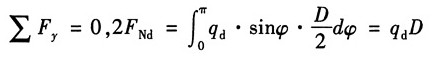
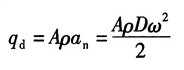
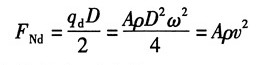
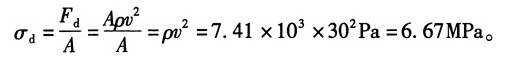
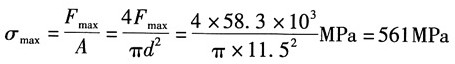
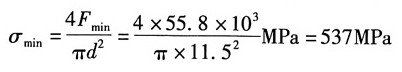
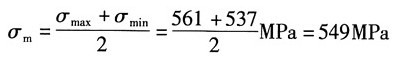
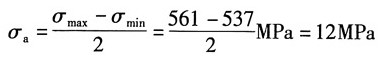
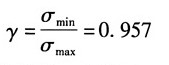

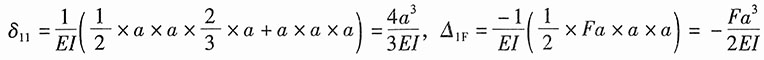
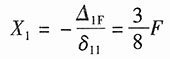


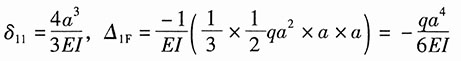
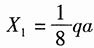
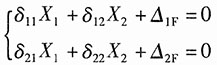

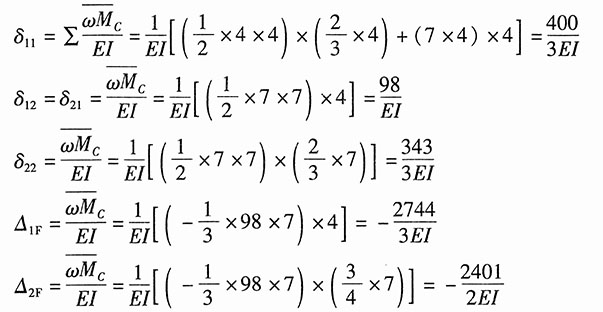



 由于AB段集中载荷的作用,该段弯矩图为抛物线,且绘制弯矩图时,将弯矩画在刚架受压一侧,如图(a)所示。
由于AB段集中载荷的作用,该段弯矩图为抛物线,且绘制弯矩图时,将弯矩画在刚架受压一侧,如图(a)所示。


