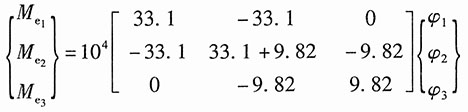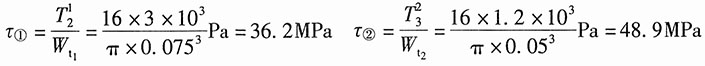计算题1. 如图所示,桥式起重机的最大载荷为W=23kN。起重机大梁为32a工字钢,E=210GPa,l=8.76m,规定
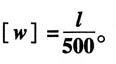
试校核大梁的刚度。
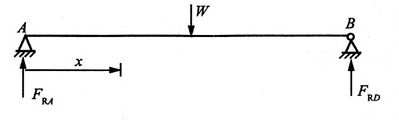
解:梁的受力简图,如图所示。
根据平衡条件可得支反力:
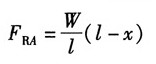
x截面处弯矩值:
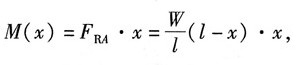
为求其最大值,令
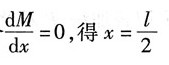
此时有最大弯矩值:
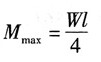
梁上的最大挠度发生在跨中截面处,查型钢表知No. 32a号工字钢截面参数I=11100cm
4 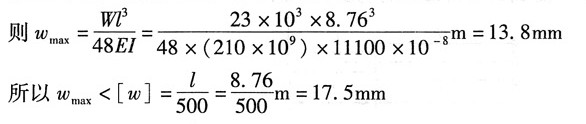
满足刚度要求。
2. 木制短柱的四角用四个40mm×40mm×4mm的等边角钢加固。已知角钢的许用应力[σ]
钢=160MPa。E
钢=200GPa;术材的许用应力[σ]
木=12MPa,E
木=10GPa。试求许可载荷F。
解:由平衡条件可得:F
钢+F
木-F=0 ①
由几何关系可知角钢和木材的变形量相等,即有变形协调条件:Δl
钢=△l
木 又由胡克定律可得:

其中,查型钢表知单个40mm×40mm×4mm角钢的横截面积:A
钢=308.6mm
2 故有:

联立式①②可得各自承受的轴力:F
钢=0.283F,F
木=0.717F
根据角钢的强度条件:

可得许可载荷:[F
1]=698kN
根据木材的强度条件:

可得许可载荷:[F
2]=1045kN
综上,许可载荷F=698kN。
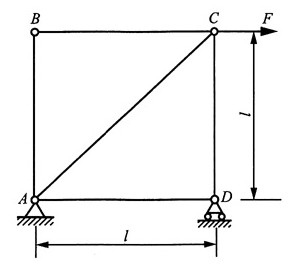
3. 如图所示桁架各杆的材料相同,截面面积相等。在载荷F作用下,试求节点B与D间的相对位移。
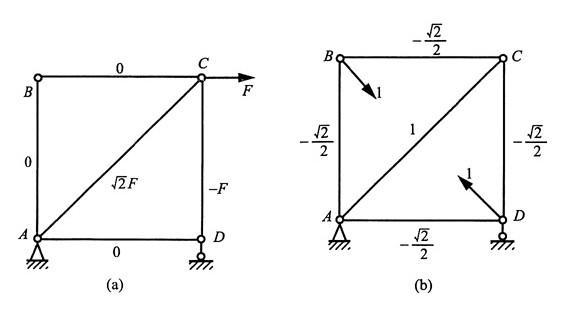
解:根据平衡条件,在已知力F作用下各杆内力,如图(a)所示。为求得B、D间相对位移,在两点处施加一对沿B、D连线的单位力,并求得此时各杆内力,如图(b)所示。
根据单位载荷法,可得B、D相对位移:
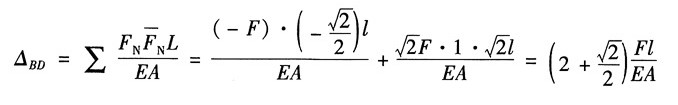
结果为正,表明和图中所施加单位载荷的方向一致,即节点B、D相互靠近。
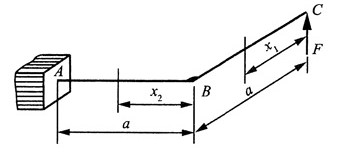
4. 在图所示曲拐的端点C上作用集中力F。设曲拐两段材料相同且均为同一直径的圆截面杆,试求C点的垂直位移。
解:曲拐总的应变能由AB段、BC段的弯曲应变能和AB段的扭转应变能三部分组成,即:
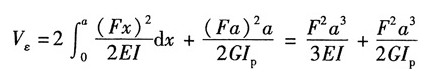
由卡氏定理,可得C点的垂直位移:
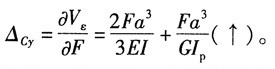
5. 已知:
(a)ε
x=-0.00012,ε
y=0.00100,γ
xy=0.00020
(b)ε
x=0.00060,ε
y=-0.00020,γ
xy=-0.00080
试求主应变及其方向。
解:(a)根据主应变计算公式:
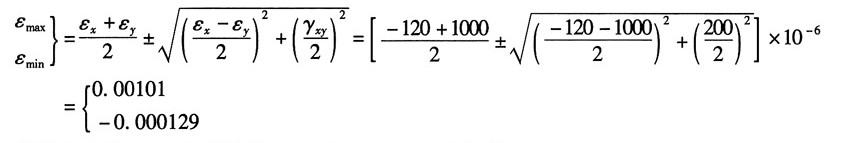
则主应变为:ε
1=0.00101,ε
2=0,ε
3=-0.000129
方向:
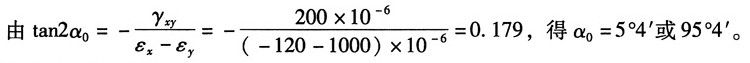
(b)根据主应变计算公式:

则主应变为:ε
1=0.00077,ε
2=0,ε
3=-0.00037
方向:
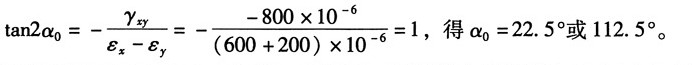
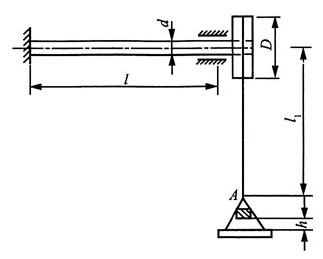
6. 如图所示圆轴直径d=6cm,l=2m,左端固定,右端有一直径D=40cm的鼓轮。轮上绕以钢绳,绳的端点A悬挂吊盘。绳长l
1=10m,横截面面积A=1.2cm
2,E=200GPa。轴的切变模量G=80GPa。重量P=800N的物块自h=20cm处落于吊盘上,求轴内最大切应力和绳内最大正应力。
解:当P从静载荷作用于托盘上时,由轴扭转引起重物的静位移:
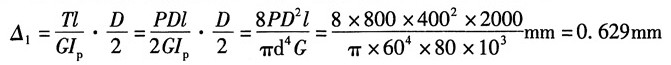
绳的伸长量:
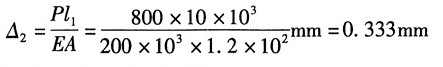
故重物总位移:Δ
st=Δ
1+Δ
2=0.962mm
由此可得自由落体冲击作用下动荷系数:
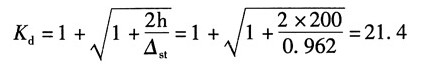
故轴内最大切应力为:
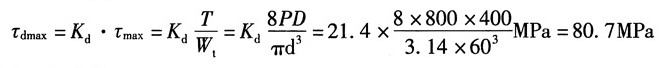
绳内最大正应力为:
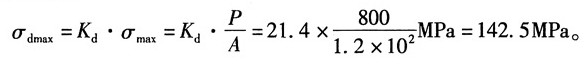
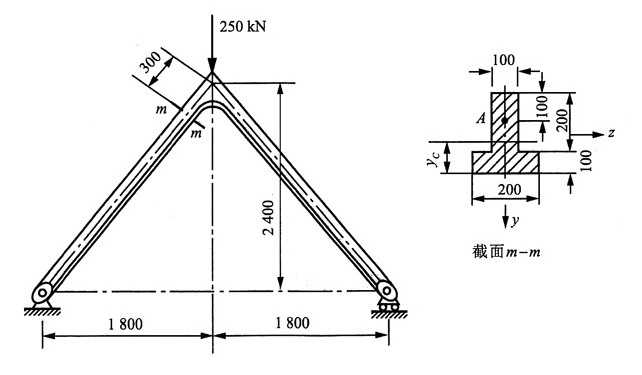
7. 人字架及承受的载荷如图所示。试求截面m-m上最大正应力和该截面上A点的正应力。
解:求m-m截面的形心:
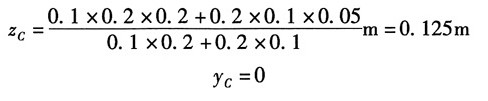
横截面对中性轴的惯性矩:
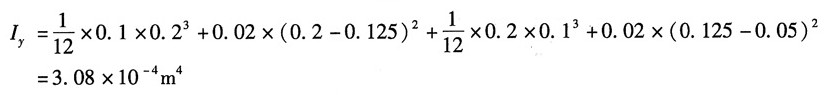
假想沿m-m截面将该结构断开,根据平衡条件求得m-m截面上的内力为:
F
N=100kN,F
S=75.1kN,M=203kN·m
故该截面上最大正应力:
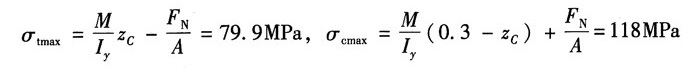
A点的正应力:
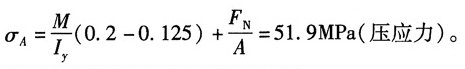
8. 炮筒内直径为150mm,外直径为250mm。射击时筒内气体的最大压力为p
1=120MPa。试求炮筒内侧面的周向应力及径向应力。
解:炮筒属于只有内压的情况,且
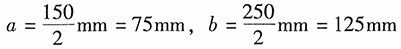
,ρ=a=75mm,p
1=120MPa。
由只有内压厚壁圆筒的应力计算公式得:
径向应力
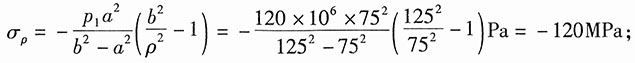
周向应力
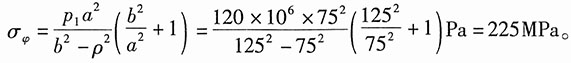
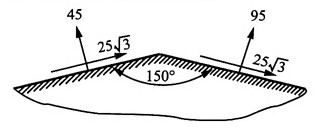
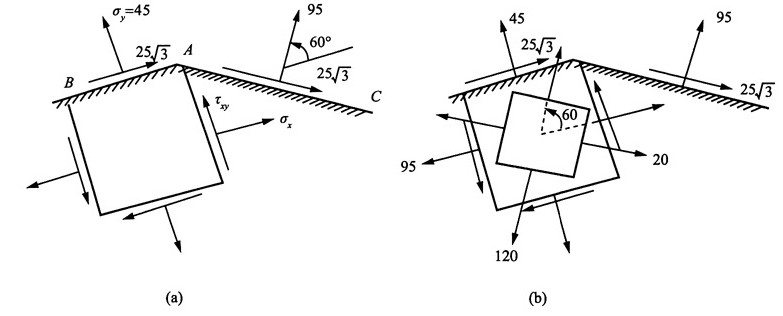
9. 在通过一点的两个平面上,应力如图所示,单位为MPa,试求主应力的大小及主平面的位置,并用单元体的草图表示出来。
解:选取如图(a)所单元体,则有:
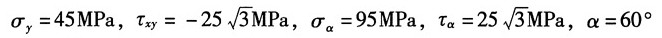
由斜截面应力计算公式
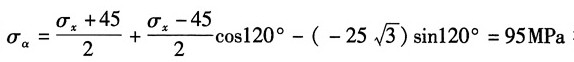
得:σ
x=95MPa
由主应力计算公式得:
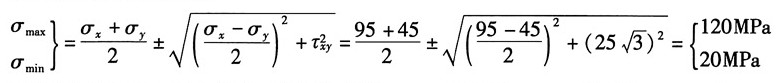
根据主应力标记符号规定,记主应力为:σ
1=120MPa,σ
2=20MPa,σ
3=0
主平面位置:由
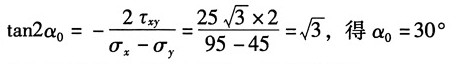
综上,单元体主应力及其位置表示如图(b)所示。
10. T形截面的曲杆如图1所示。设F=450N,l=70cm,R=20cm。试绘出截面m-m上的应力分布图。
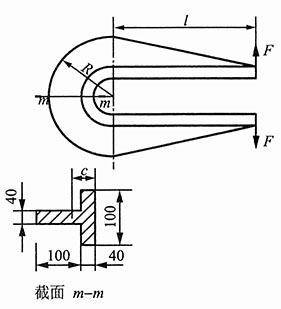
图1
解:截面形心到截面内侧边缘的距离:
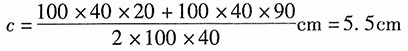
则T截面可看作是两个矩形组成的截面,其上纤维的曲率半径分别为:
R
1=20cm,R
2=R
1-14=6cm,R
3=20-10cm=10cm
轴线曲率半径:R
0=R
2+c=6+5.5cm=11.5cm
则
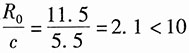
,为大曲率杆。
又两矩形截面:b
2=4cm,b
3=10cm,h
2=10cm,h
3=4cm
面积:A=2×100×40=8×10
3mm
2=8×10
-3m
2
故曲杆中性层曲率半径:
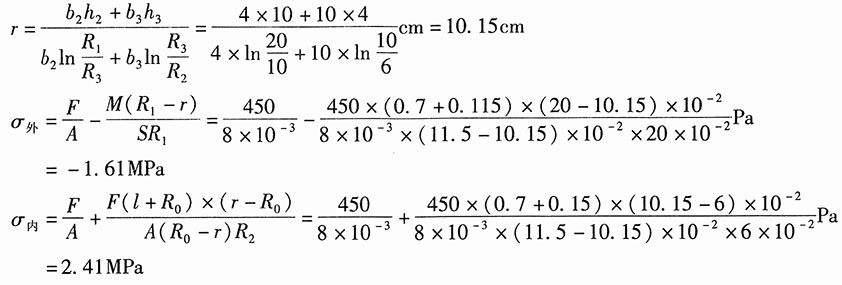
该截面的应力分布如图2所示。

图2
11. 测定材料剪切强度的剪切器的示意图如图所示。设圆试样的直径d=15mm,当压力F=31.5kN时,试样被剪断,试求材料的名义剪切极限应力。若取剪切许用应力为[τ]=80MPa,试问安全因数是多大?
解:如图所示,由试件受力部分的分析可知,试件横截面上承受的剪力

该试件的名义剪切极限应力:

由许用应力的定义

可得安全因数:

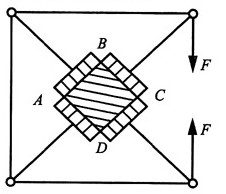
12. 立方块ABCD尺寸是70mm×70mm×70mm,通过专用的压力机在其四个面上作用均匀分布的压力。若F=50kN,E=200GPa,μ=0.30,试求立方块的体应变θ。
解:由静力学平衡条件可得方块的四个面上受到的压力均为
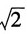
F,故在四个面上的压应力均为:
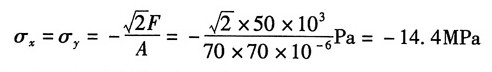
剩余一对平面上不受力,故σ
z=0。
而方块的六个面上均无切应力,这些面都是主平面,故主应力为:
σ
1=0,σ
2=σ
3=-14.4MPa
则方块的体应变为:
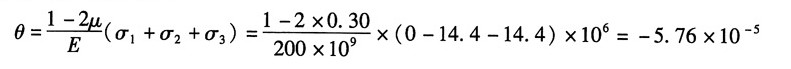
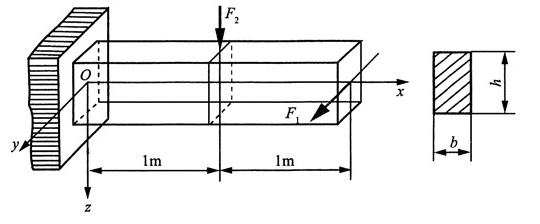
13. 作用于下图所示悬臂木梁上的载荷为:在水平平面内F
1=800N,在垂直平面内,F
2=1650N。木材的许用应力[σ]=10MPa。若矩形截面h/b=2,试确定其尺寸。
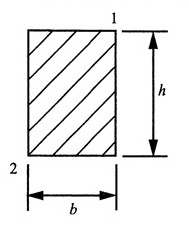
解:固定端处截面为危险截面,且危险点为1、2点,如图所示。
固定端截面的弯矩:M
y=F
2×1=1650×1N·m=1650N·m
M
z=F
1×2=800×2N·m=1600N·m
根据强度条件:
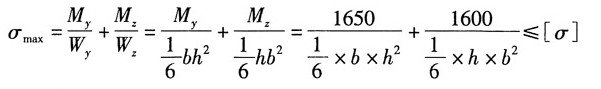
且
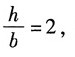
解得:
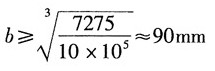
故取截面尺寸:b=90mm,h=2b=180mm。
14. 试求图1所示各应力状态的主应力及最大切应力(应力单位为MPa)。
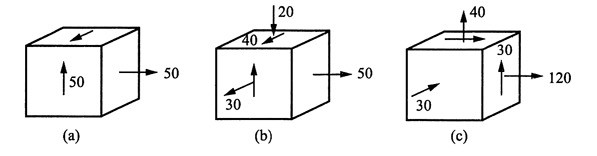 图1
图1
解:对图1分别建立如图2所示坐标系。
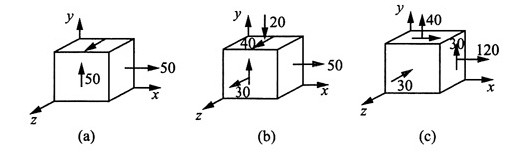 图2
图2 (a)已知σ
x=50MPa,σ
y=σ
z=0,τ
yz=50MPa,其中σ
x=50MPa为主应力。
又根据主应力计算公式:
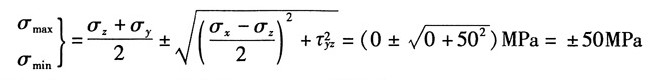
可得主应力为:σ
1=σ
2=50MPa,σ
3=-50MPa
故最大切应力为:
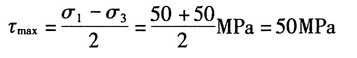
(b)已知σ
x=50MPa,σ
y=-20MPa,σ
z=30MPa,τ
yz=40MPa,其中σ
x=50MPa为主应力。
又根据主应力计算公式:
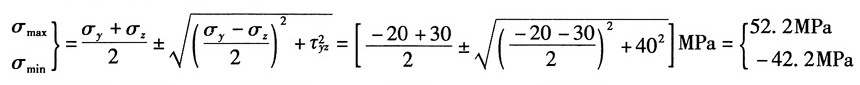
可得主应力为:σ
1=52.2MPa,σ
2=50MPa,σ
3=-42.2MPa
故最大切应力为:
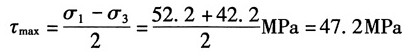
(c)已知σ
x=120MPa,σ
y=40MPa,σ
z=-30MPa,τ
xy=-30NPa,其中σ
z=-30MPa为主应力。
又根据主应力计算公式:
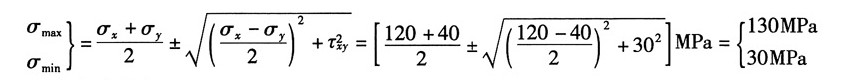
可得主应力为:σ
1=130MPa,σ
2=30MPa,σ
3=-30MPa
故最大切应力为:

15. 等截面钢梁直径d=50mm,E=200GPa。求节点位移和支座反力,并作弯矩图。
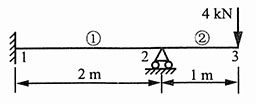
图1
解:把梁看作是①、②两单元组成的杆系,分别写出两个单元的单元刚度矩阵。
单元①:
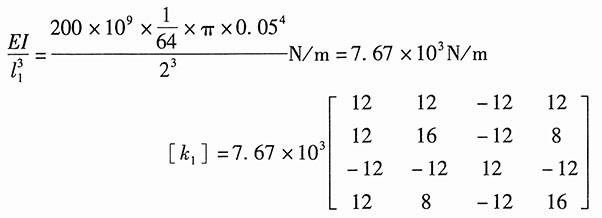
单元②:
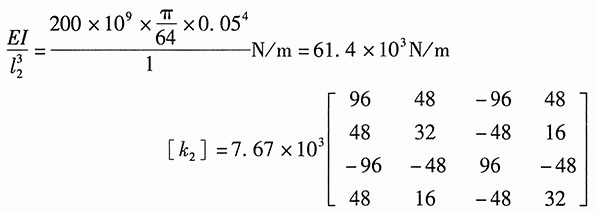
根据梁支座条件,可得节点位移:{δ}=(0 0 0 θ
2 ω
3 θ
3)
T
节点力:{F}=[Y
1 M
1 Y
2 0 -4×10
3 0]
T
由①、②的单元刚度矩阵[k
1]、[k
2]叠加生成的整体刚度矩阵[k],并代入整体刚度方程{F}=[k]{δ}得:
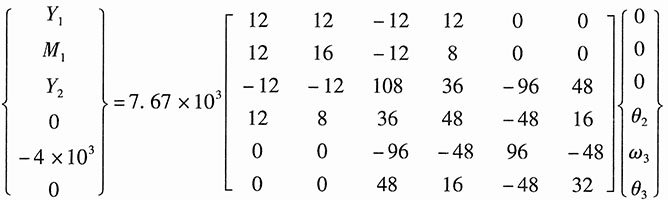
则节点位移:
θ
2=-0.0326rad
ω
3=-54.3mm
θ
3=-0.0625rad
支座反力:
Y
1=3kN(↓)
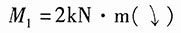
Y
2=7kN(↑)
由此可作弯矩图,如图2所示。
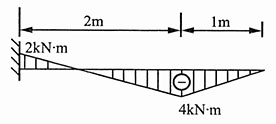
图2
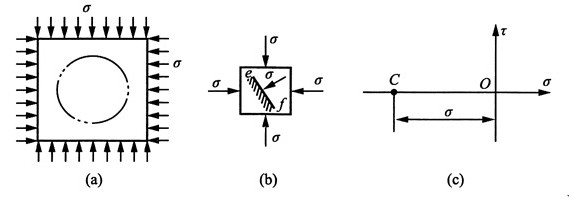
16. 若物体在两个方向上受力相同,如图(a)所示,试分析物体内任一点的应力状态。
解:在这种情况下,物体内任意一点的应力状态皆如图(b)所示。代表这一应力状态的应力圆如图(c)所示退缩成一点C,半径等于零。单元体任意斜面ef上的正应力都等于σ,切应力都等于零。这样,如从物体中任意地割取一部分,例如从中分割出一个圆柱体,则在圆柱体的柱面上的正应力也都是σ。
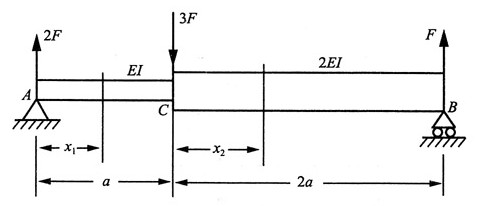
17. 试用积分法求图所示阶梯形变截面梁的挠曲线方程、端截面转角和最大挠度。
解:(1)取AC段为研究对象
原点放到A点,当0≤x
1≤a时,有
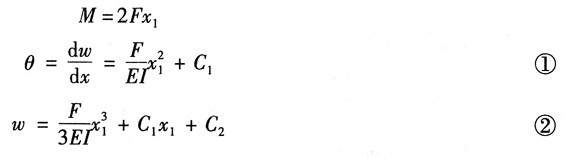
根据边界条件:x
1=0时,θ=θ
A,ω=0,可得:C
1=θ
A,C
2=0
将积分常数的值代入式①②,令x
1=a,可得截面c的转角和挠度分别为
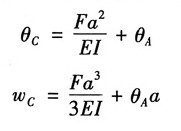
(2)取CB段为研究对象
原点放到C点,当0≤x
2≤2a时,有

根据边界及连续性条件:x
2=0,θ=θ
C,w=w
C,可得
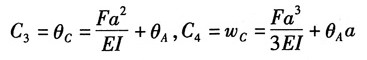
将积分常数的值代入式③④,可得
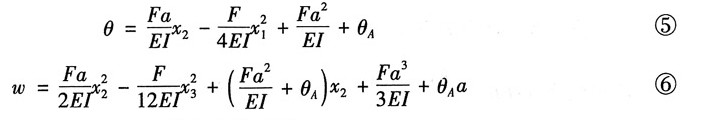
根据边界条件:x
2=2a,w=w
B=0,代入式⑥可得
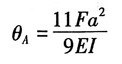
将上式代入①式、②式、⑤式和⑥式,得变截面梁的转角和挠度方程
AC段:
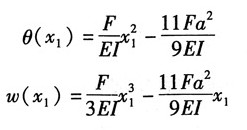
CB段:
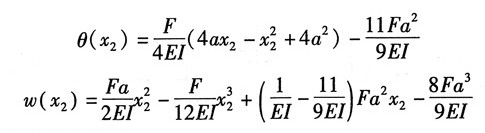
(3)求端界面转角和最大挠度
断面转角:当x
1=0时,

当x
2=2a时,
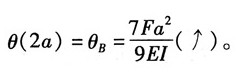
最大挠度处θ=0,由方程可知一定在CB段。
令θ(x
2)=0,可得:x
2=0.211a
故最大挠度
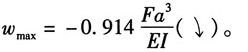
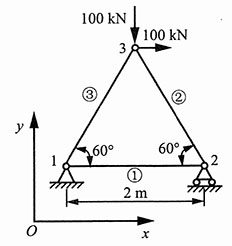
18. 图1所示桁架各杆横截面面积均为800mm
2,且均为钢杆,E=210GPa。试求桁架各杆的内力和各节点的位移。
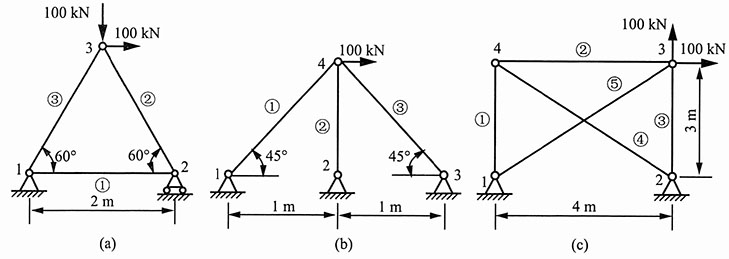
图1
解:(1)图1(a)所示
建立如图2所示坐标系。
首先写出各单元的单元刚度矩阵。
对于各杆均有:
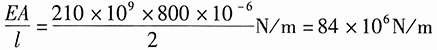
单元①,θ=0°,根据公式得整体坐标系中的单元刚度矩阵:
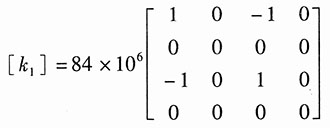
单元②,θ=120°,根据公式得整体坐标系中的单元刚度矩阵:

单元③,θ=60°,根据公式得整体坐标系中的单元刚度矩阵:
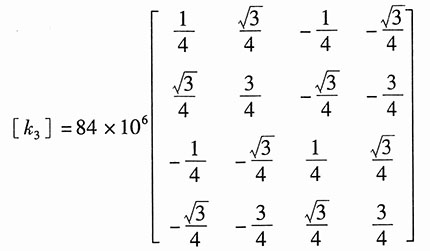
由此可列出整体刚度方程为:

由桁架的支座条件知:u
1=ω
1=ω
2=0
又已知节点3载荷:F
X3=100kN,F
Y3=-100kN,F
X2=0
代入整体刚度矩阵可得:u
2=0.938mm,u
3=2.85mm,ω
3=-1.06mm
即节点位移:[u
1 ω
1 u
2 ω
2 u
3 ω
3]
T=[0 0 0.938 0 2.85 -1.06]
T
将以上求得的各点位移代回刚度方程,司得节点载荷:
[F
X1 F
Y1 F
X2 F
Y2 F
X3 F
Y3]
T=[-100 -36.8 0 136.8 100 -100]
T
即为各支座反力。
由此,经坐标转化,可求得各杆内力:
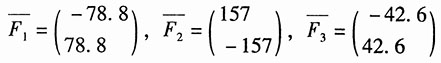
。
(2)图1(b)所示
同理,各杆内力:
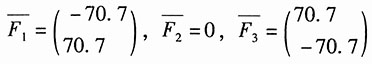
各节点位移:
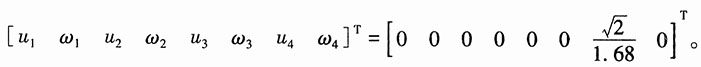
(3)图1(c)所示
同理,各杆内力:
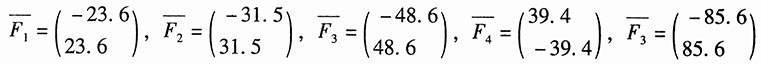
各节点位移:
[u
1 ω
1 u
2 ω
2 u
3 ω
3 u
4 ω
4]
T=[0 0 0 0 2.533 0.869 1.783 0.422]
T。
19. 如图所示的三角形薄板因受外力作用而变形,角点B铅垂向上的位移为0.03mm,但AB和BC仍保持为直线。试求沿OB的平均应变,井求AB与BC两边在B点的角度改变。
解:如图所示,由线应变的定义可知,沿OB方向的平均应变为:

变形后AB与BC两边的角度改变量为:

γ
B非常微小,由图示几何关系有:

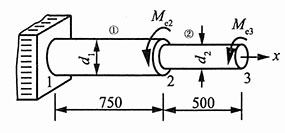
20. 变截面钢轴上的M
e2=1.8kN·m,M
e3=1.2kN·m,直径d
1=75mm,d
2=50mm,材料的切变模量G=80GPa。试求最大切应力和左右两端的相对扭转角。
解:把杆件看作是①、②两个单元,分别写出两个单元的单元刚度方程。
单元①:
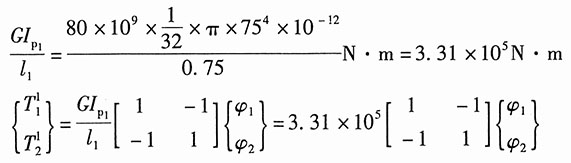
单元②:

由1、2、3三节点的平衡,可得:
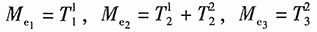
将单元刚度方程中的
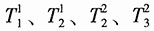
代入以上平衡方程,可得整体刚度方程:
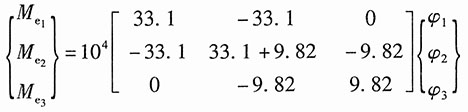
固定节点1的位移φ
1=0,且将M
e2=1.8kN·m,M
e3=1.2kN·m代入整体刚度方程可得:φ
2=9.06×10
-3rad,φ
3=2.1×10
-2rad。
故左右两端相对扭转角:φ
3=21×10
-3rad
各段切应力:
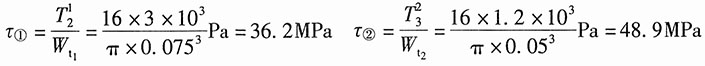
综上,最大切应力发生在单元②,即τ
max=τ
②=48.9MPa。
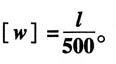 试校核大梁的刚度。
试校核大梁的刚度。
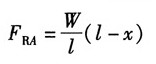
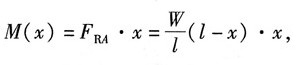 为求其最大值,令
为求其最大值,令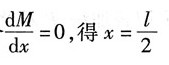
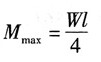
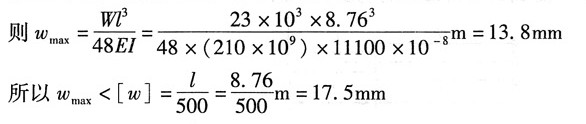





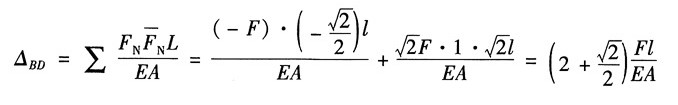
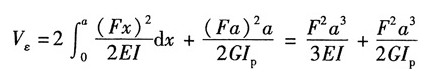
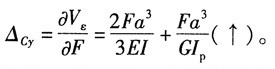
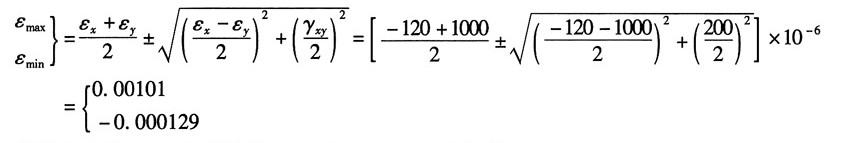
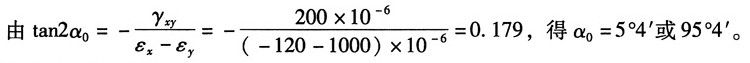

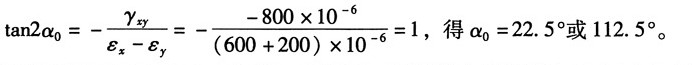
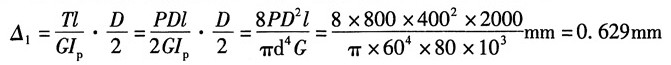
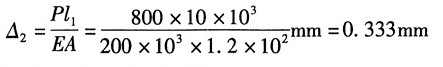
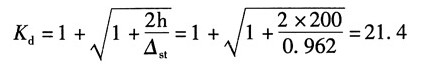
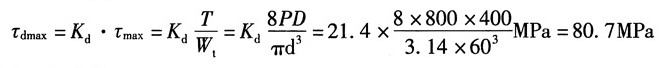
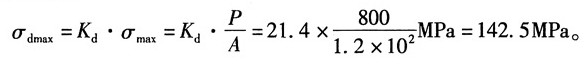
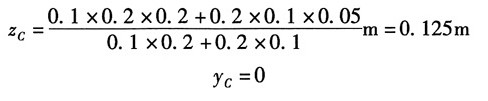
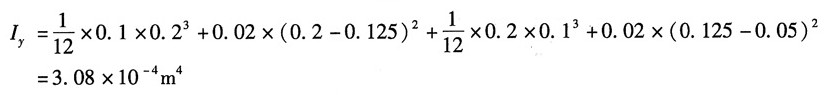
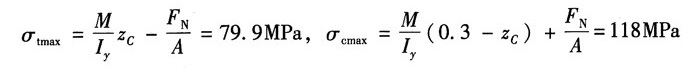
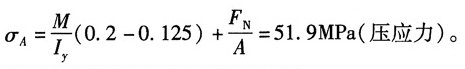
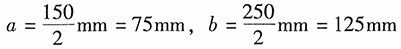 ,ρ=a=75mm,p1=120MPa。
,ρ=a=75mm,p1=120MPa。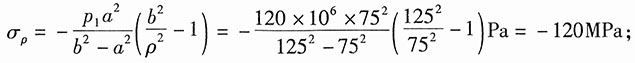
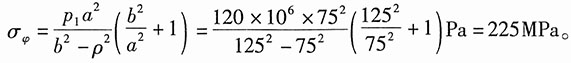
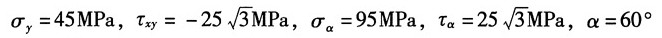
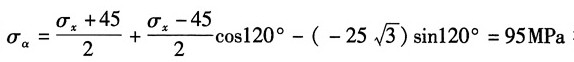 得:σx=95MPa
得:σx=95MPa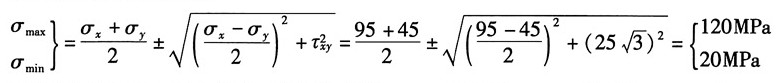
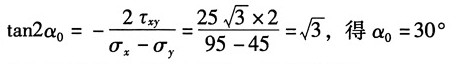

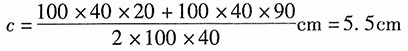
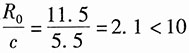 ,为大曲率杆。
,为大曲率杆。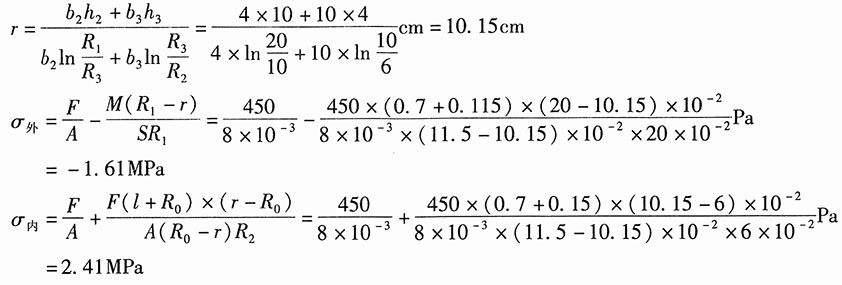





 可得安全因数:
可得安全因数:
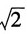 F,故在四个面上的压应力均为:
F,故在四个面上的压应力均为: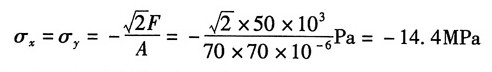
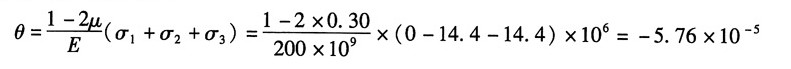
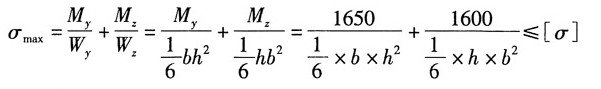
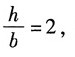 解得:
解得: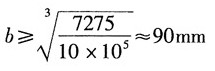


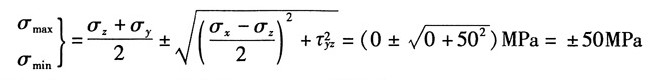
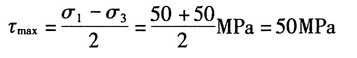
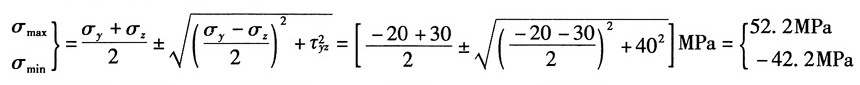
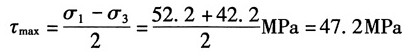
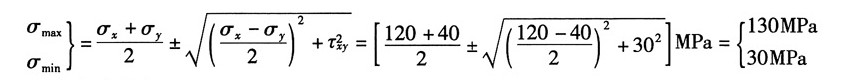


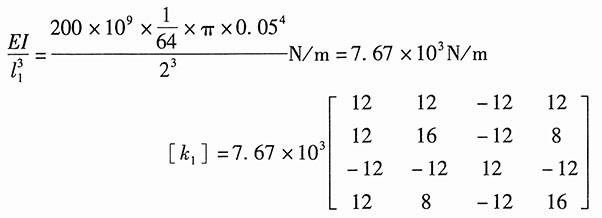
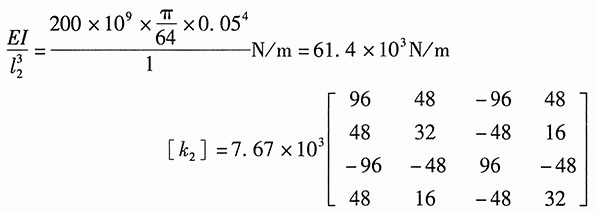

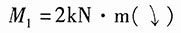

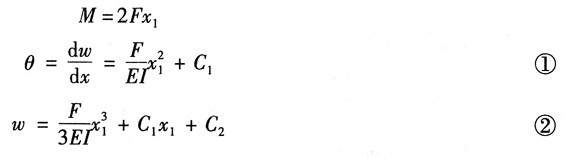
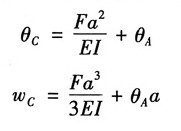

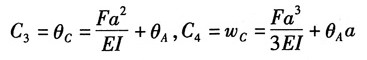
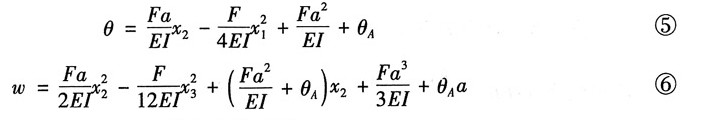
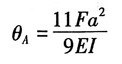
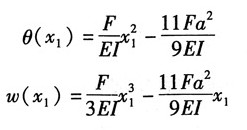
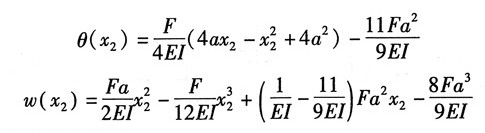
 当x2=2a时,
当x2=2a时,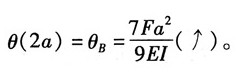
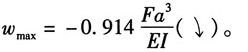

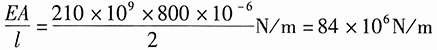
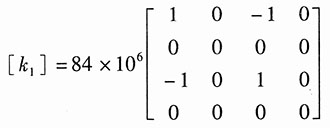

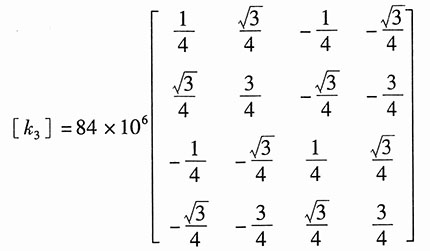

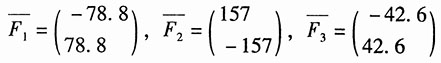 。
。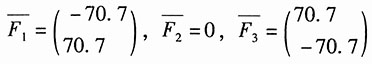
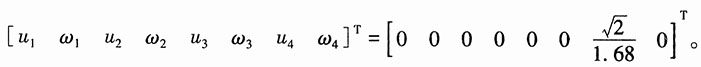
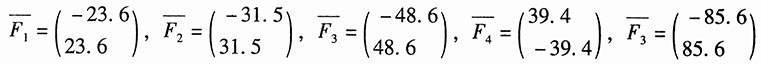





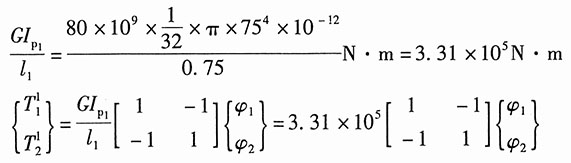

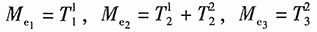
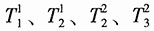 代入以上平衡方程,可得整体刚度方程:
代入以上平衡方程,可得整体刚度方程: