一、选择题在每小题的四个备选答案中选出一个正确答案.1. 下列无穷级数收敛的是______
A.
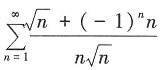
B.
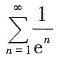
C.

D.

A B C D
B
[解析] A项,
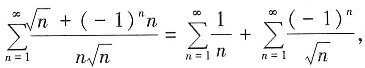
其中调和级数
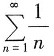
发散,而
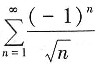
为交错级数,收敛,所以原级数发散;
B项,
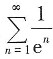
为等比级数,其中
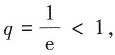
级数收敛;
C项,由级数收敛的必要条件知
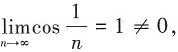
级数发散;
D项,
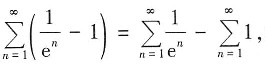
级数
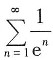
收敛,级数
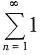
发散,所以原级数发散。故选B。
2. 设极限
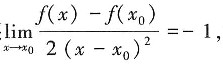
则点x=x
0是函数f(x)的______
- A.极大值点
- B.极小值点
- C.驻点但非极值点
- D.非驻点
A B C D
A
[解析] 由题可知,当x→x
0时,
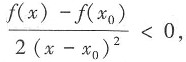
又(x-x
0)
2>0,从而在x
0的邻域内,f(x)-f(x
0)<0,即f(x)<f(x
0),由极值的定义可知,x=x
0是f(x)的极大值点。故选A。
4. 设f(x)在点x
0的某邻域内有定义,则f(x)在点x
0处可导的一个充分条件是______
A.
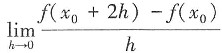
存在
B.
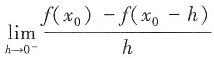
存在
C.
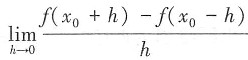
存在
D.
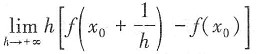
存在
A B C D
A
[解析] B项只有左导数存在;D项只有右导数存在;C项极限存在不能推出每部分极限都存在。故选A。
6. 若向量a,b的模分别为|a|=2,|b|=
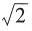
,且a·b=2,则|a×b|=______
A.2
B.

C.
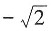
D.1
A B C D
A
[解析] 由题意知
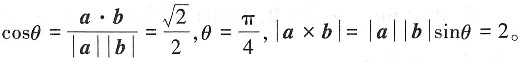
7. 极限
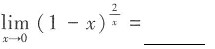
A.

B.
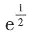
C.e
-2 D.e
2 A B C D
C
[解析]
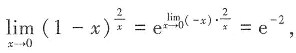
故选C。
8. 由方程y-xe
y=1所确定的隐函数y=y(x)的导数
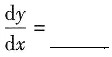
A.
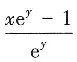
B.
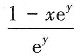
C.
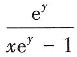
D.
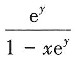
A B C D
D
[解析] 令F(x,y)=y-xe
y-1,则F'
x=-e
y,F'
y=1-xe
y,故
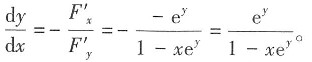
9. 若
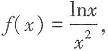
则f'(1)=______
A.0
B.ln2
C.
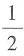
D.1
A B C D
D
[解析]
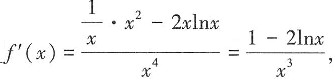
即f'(1)=1,故选D。
16. 设函数f(x)在点x=x
0处可导,且f'(x
0)=1,则
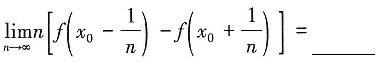
A.-2
B.2
C.
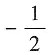
D.
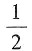
A B C D
A
[解析]
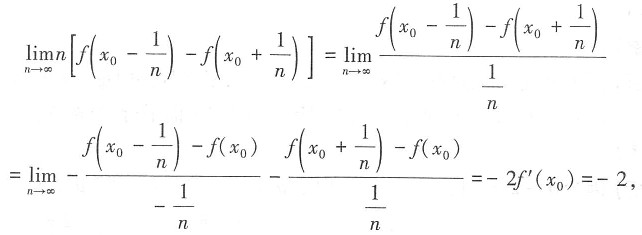
故选A。
20. 设函数
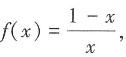
g(x)=1-x,则f[g(x)]=______
A.
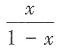
B.
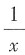
C.
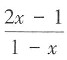
D.2+x
A B C D
A
[解析]
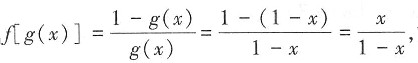
故选A。
21. 下列级数条件收敛的是______
A.
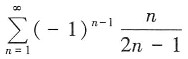
B.
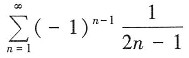
C.
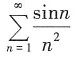
D.
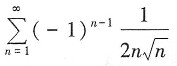
A B C D
B
[解析] A项不对,因为
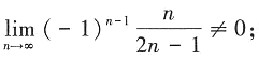
C项中
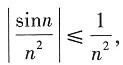
因为
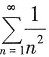
收敛,根据比较审敛法可知,
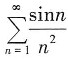
绝对收敛;D项中当n→∞时,
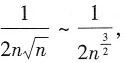
因为
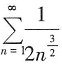
收敛,根据比较审敛法极限形式可知,
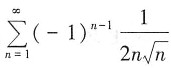
绝对收敛;B项中
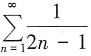
发散,又根据莱布尼茨判别法可知
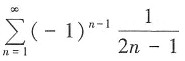
收敛,故
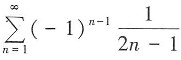
条件收敛。
23. 设f(x)=sinx,则

A.
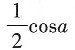
B.
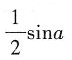
C.2cosa
D.2sina
A B C D
A
[解析]
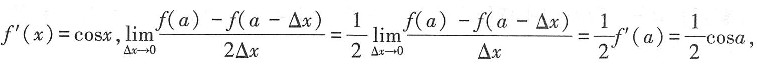
故选A。
29. 微分方程
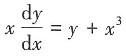
的通解是y=______
A.
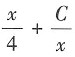
B.
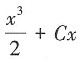
C.

D.
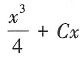
A B C D
B
[解析]
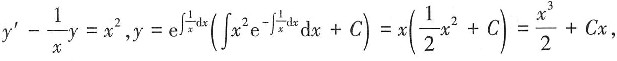
故选B。
二、填空题1. 设向量b与向量a={1,-2,-1}平行,且a·b=12,则b=______。
{2,-4,-2}
[解析] 因为a//b,设b=ka=k{1,-2,-1},则a·b=k{1+4+1}=12,k=2,即b=2a={2,-4,-2}。
2. 极限
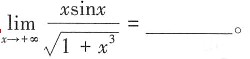
0
[解析] 根据无穷小的性质可知,
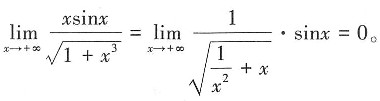
3. 不定积分
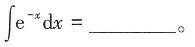
-e-x+C
[解析]
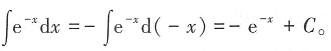
4. 向量a={4,-3,4}在b={2,2,1}上的投影为______。
2
[解析] 向量a在b上的投影为
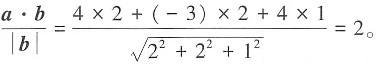
5. 非齐次微分方程y"-5y'+6y=xe
2x的一个特解应设为______。
y=x(Ax+B)e2x(A,B为待定系数)
[解析] 方程对应二阶齐次线性微分方程的特征方程为r2-5r+6=0,所以r1=2,r2=3,λ=2是该特征方程的一个特征根,所以特解形式为y=x(Ax+B)e2x(A,B为待定系数)。
6. 已知连续函数f(x)满足
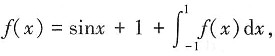
则f(x)=______。
sinx-1
[解析] 令
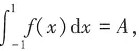
则f(x)=sinx+1+A,两边同时积分,得
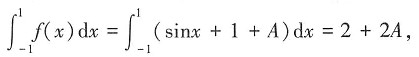
则2+2A=A,即A=-2,则f(x)=sinx-1。
7. 设函数
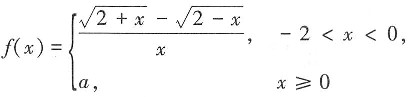
在x=0处连续,则必有a=______。
8. 幂级数
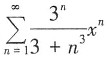
的收敛半径为______。
[解析]
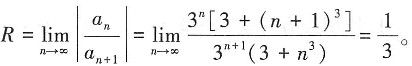
10. 设D为圆环域1≤x
2+y
2≤4,则二重积分
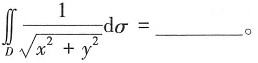
2π
[解析]
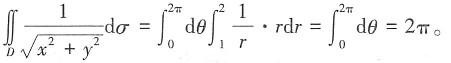
三、计算题(每小题5分,共50分)1. 求微分方程
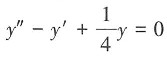
的通解。
解:该微分方程对应的特征方程为
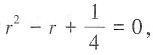
则
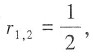
则该微分方程的通解为
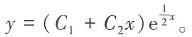
3. 求极限
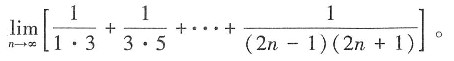
解:
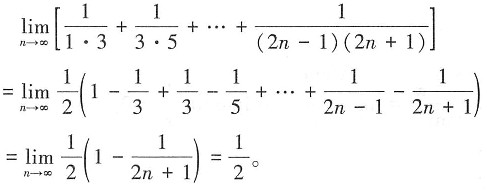
4. 求定积分
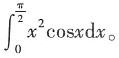
解:
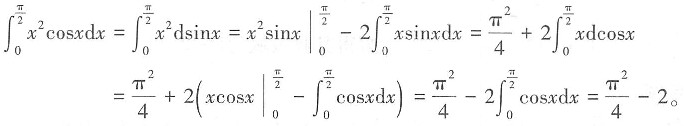
5. 设方程e
-xy-2z+e
z=0确定隐函数z=z(x,y),求
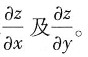
解:设F(x,y,z)=e
-xy-2z+e
z,
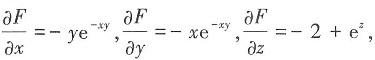
所以
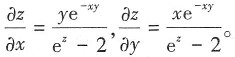
6. 计算曲线积分
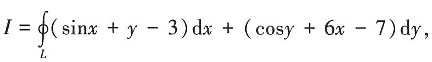
其中L为顶点分别为(0,0)、(2,0)、(2,1)和(0,1)的四边形区域D的正向边界。
解:令P(x,y)=sinx+y-3,Q(x,y)=cosy+6x-7,则
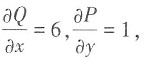
由格林公式可得
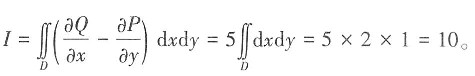
8. 求幂级数
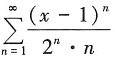
的收敛区间。
解:因为
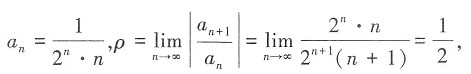
所以R=2,从而-2<x-1<2,故收敛区间为(-1,3)。
9. 计算二重积分
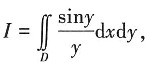
其中积分区域D是由y=x,
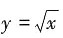
所围成的闭区域。
解:y=x,y=
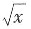
的交点为(0,0)和(1,1),则积分区域如图所示,
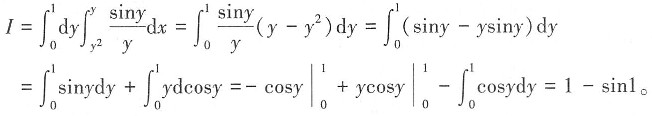
10. 求由方程
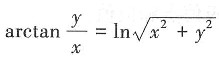
确定的隐函数y=y(x)的导数。
解:方程两边同时对x求导得,
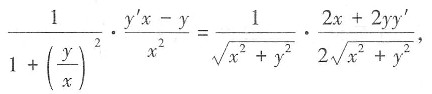
化简得
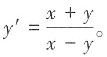
四、应用题(每小题7分,共14分)1. 为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
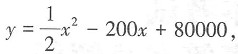
且每处理一吨二氧化碳得到可利用的化工产品价值为100元。该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
设该单位每月获利为S,则
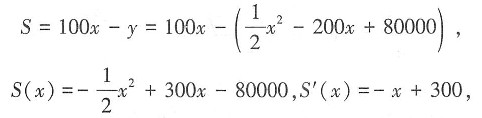
因为当400≤x≤600时,S'(x)<0,S(x)单调递减,所以当x=400时,S有最大值-40000。故该单位不获利,需要国家每月至少补贴40000元,才能不亏损。
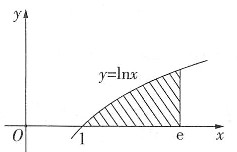
2. 求由曲线y=lnx,x=e与y=0所围成的平面图形的面积S,并求该平面图形绕x轴旋转所形成旋转体的体积V。
由y=lnx.x=e与y=0得交点为(1,0),(e,0),(e,1),如图所示,
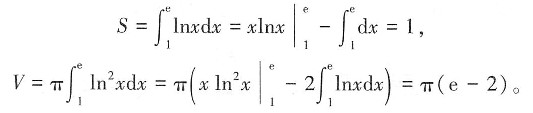
五、证明题(6分)1. 设函数f(x)在[0,2]上连续,在(0,2)内可导,且f(0)=1,f(1)+2f(2)=3。证明:存在ξ∈(0,2),使得f'(ξ)=0。
证:因为f(x)在[1,2]上连续,所以f(x)在[1,2]上取得最小值m和最大值M,即3m≤f(1)+2f(2)≤3M,得m≤1≤M,由介值定理可知,存在一点c∈[1,2],使得f(c)=1。又f(x)在[0,2]上连续,在(0,2)内可导,且f(0)=f(c)=1,由罗尔定理可知,存在ξ∈(0,c)

(0,2),使得f(ξ)=0。
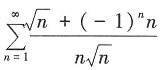
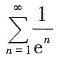


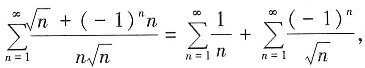 其中调和级数
其中调和级数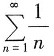 发散,而
发散,而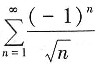 为交错级数,收敛,所以原级数发散;
为交错级数,收敛,所以原级数发散;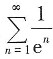 为等比级数,其中
为等比级数,其中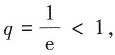 级数收敛;
级数收敛;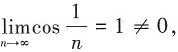 级数发散;
级数发散;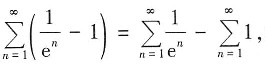 级数
级数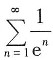 收敛,级数
收敛,级数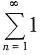 发散,所以原级数发散。故选B。
发散,所以原级数发散。故选B。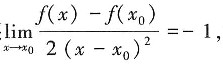 则点x=x0是函数f(x)的______
则点x=x0是函数f(x)的______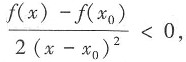 又(x-x0)2>0,从而在x0的邻域内,f(x)-f(x0)<0,即f(x)<f(x0),由极值的定义可知,x=x0是f(x)的极大值点。故选A。
又(x-x0)2>0,从而在x0的邻域内,f(x)-f(x0)<0,即f(x)<f(x0),由极值的定义可知,x=x0是f(x)的极大值点。故选A。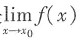 存在的______
存在的______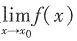 存在,则函数y=f(x)在x=x0处左、右极限都存在且相等,但反之不成立。故选B。
存在,则函数y=f(x)在x=x0处左、右极限都存在且相等,但反之不成立。故选B。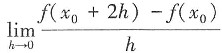 存在
存在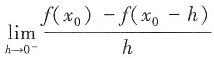 存在
存在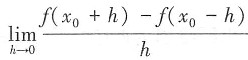 存在
存在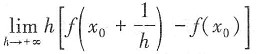 存在
存在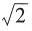 ,且a·b=2,则|a×b|=______
,且a·b=2,则|a×b|=______
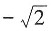
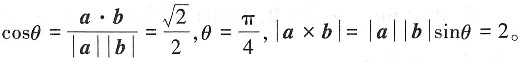
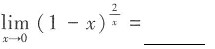

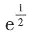
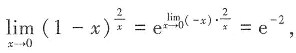 故选C。
故选C。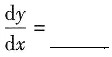
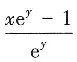
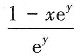
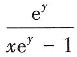
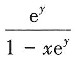
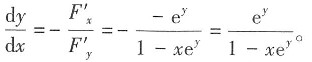
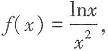 则f'(1)=______
则f'(1)=______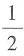
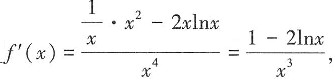 即f'(1)=1,故选D。
即f'(1)=1,故选D。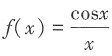 的______
的______
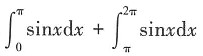
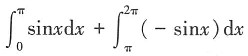
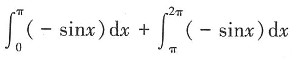
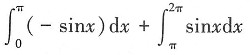
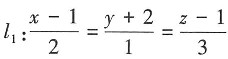 和直线
和直线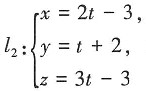 (t为参数)的位置关系为______
(t为参数)的位置关系为______ 的值是______
的值是______
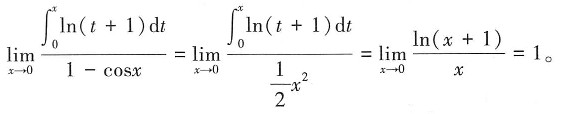 故选C。
故选C。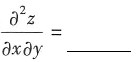
 故选D。
故选D。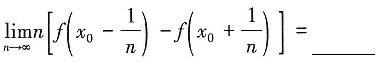
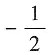
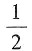
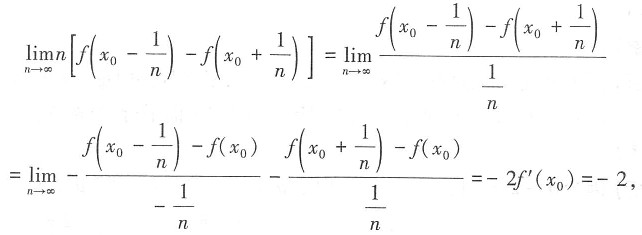
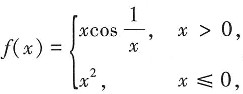 则f(x)在x=0处______
则f(x)在x=0处______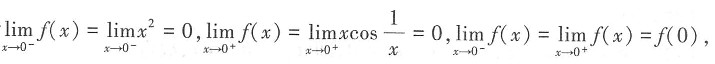 故f(x)在x=0处连续。又因为
故f(x)在x=0处连续。又因为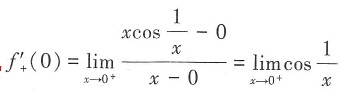 不存在,故f(x)在x=0处不可导。
不存在,故f(x)在x=0处不可导。 x=±1,可得点为(-1,2)或者(1,-2),故选C。
x=±1,可得点为(-1,2)或者(1,-2),故选C。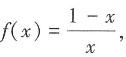 g(x)=1-x,则f[g(x)]=______
g(x)=1-x,则f[g(x)]=______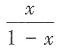
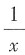
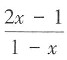
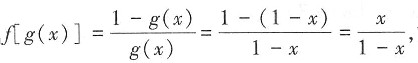 故选A。
故选A。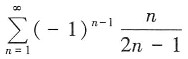
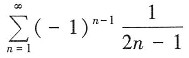
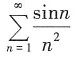
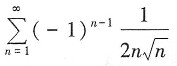
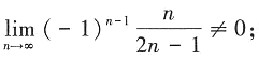 C项中
C项中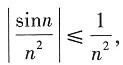 因为
因为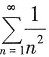 收敛,根据比较审敛法可知,
收敛,根据比较审敛法可知,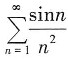 绝对收敛;D项中当n→∞时,
绝对收敛;D项中当n→∞时,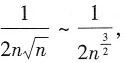 因为
因为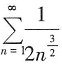 收敛,根据比较审敛法极限形式可知,
收敛,根据比较审敛法极限形式可知,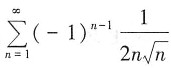 绝对收敛;B项中
绝对收敛;B项中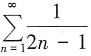 发散,又根据莱布尼茨判别法可知
发散,又根据莱布尼茨判别法可知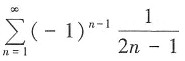 收敛,故
收敛,故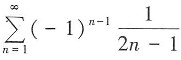 条件收敛。
条件收敛。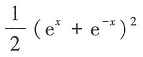
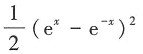
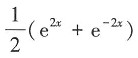
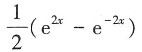
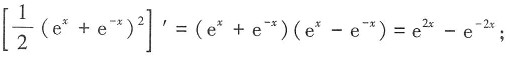

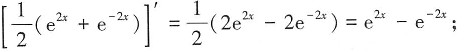
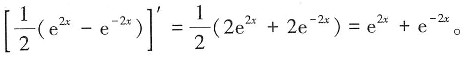 故选D。
故选D。
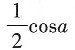
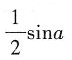
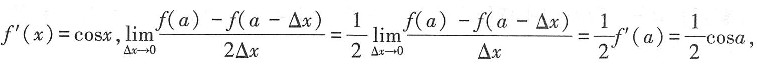 故选A。
故选A。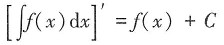
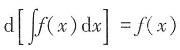
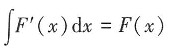
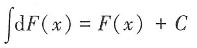
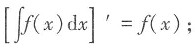 选项B,
选项B,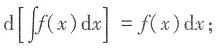 选项C,
选项C, 故选D。
故选D。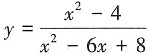 的第二类间断点为______
的第二类间断点为______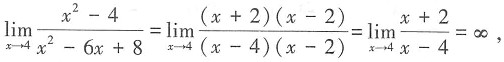 故x=4为函数的第二类间断点(无穷间断点)。
故x=4为函数的第二类间断点(无穷间断点)。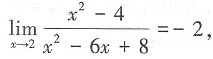 故x=2是第一类间断点。
故x=2是第一类间断点。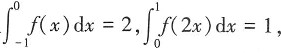 则
则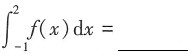
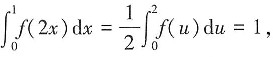 从而
从而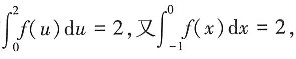 则
则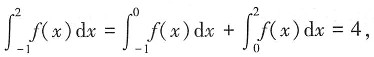
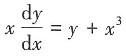 的通解是y=______
的通解是y=______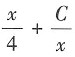
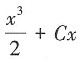

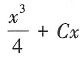
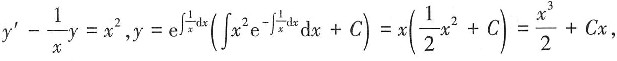 故选B。
故选B。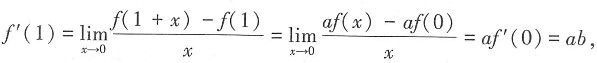 故选D。
故选D。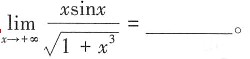
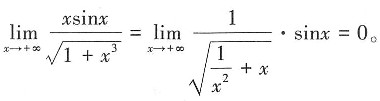
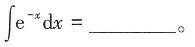
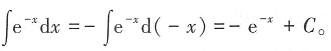
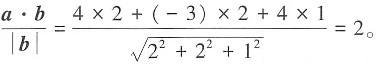
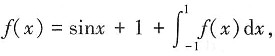 则f(x)=______。
则f(x)=______。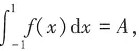 则f(x)=sinx+1+A,两边同时积分,得
则f(x)=sinx+1+A,两边同时积分,得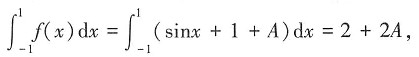
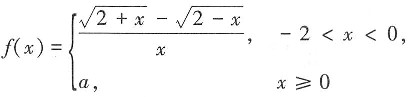 在x=0处连续,则必有a=______。
在x=0处连续,则必有a=______。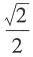
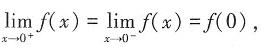 即只需要计算
即只需要计算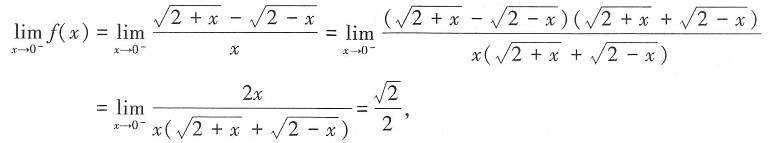
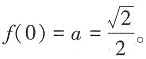
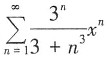 的收敛半径为______。
的收敛半径为______。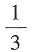
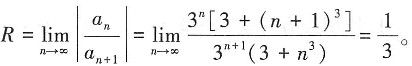
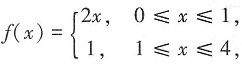 则
则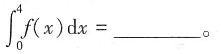
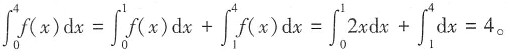
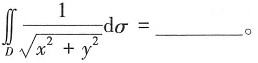
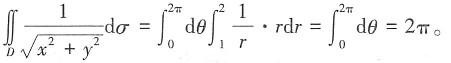
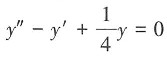 的通解。
的通解。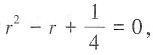 则
则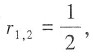 则该微分方程的通解为
则该微分方程的通解为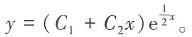
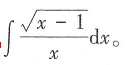
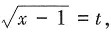 x=t2+1,则
x=t2+1,则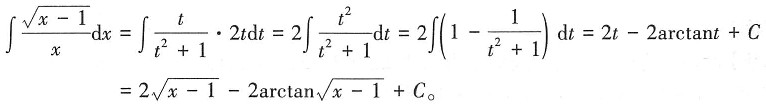
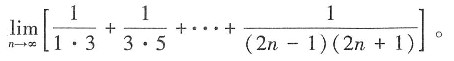
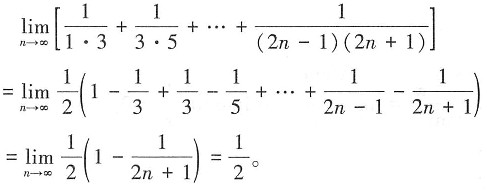
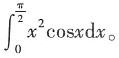
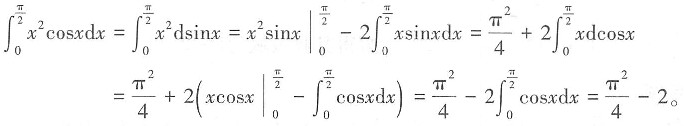
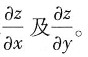
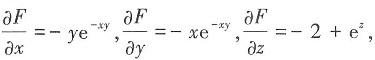 所以
所以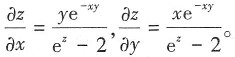
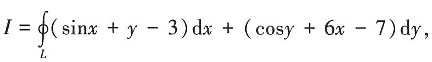 其中L为顶点分别为(0,0)、(2,0)、(2,1)和(0,1)的四边形区域D的正向边界。
其中L为顶点分别为(0,0)、(2,0)、(2,1)和(0,1)的四边形区域D的正向边界。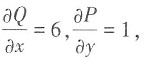 由格林公式可得
由格林公式可得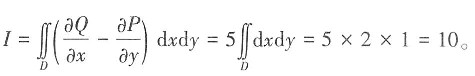
 求
求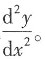
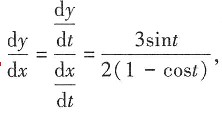 二阶导
二阶导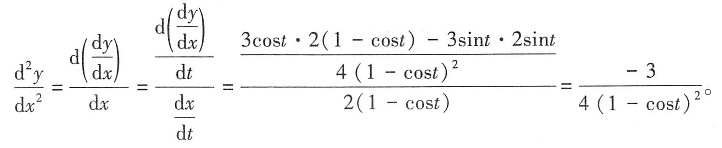
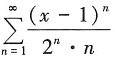 的收敛区间。
的收敛区间。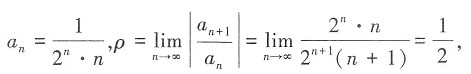
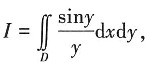 其中积分区域D是由y=x,
其中积分区域D是由y=x,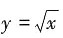 所围成的闭区域。
所围成的闭区域。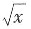 的交点为(0,0)和(1,1),则积分区域如图所示,
的交点为(0,0)和(1,1),则积分区域如图所示,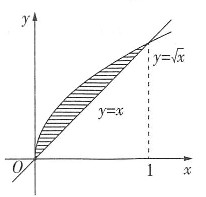
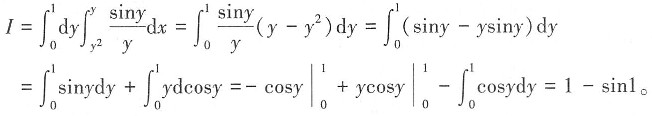
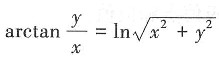 确定的隐函数y=y(x)的导数。
确定的隐函数y=y(x)的导数。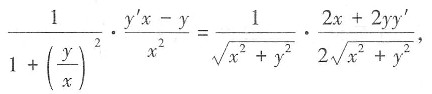
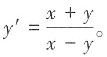
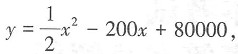 且每处理一吨二氧化碳得到可利用的化工产品价值为100元。该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
且每处理一吨二氧化碳得到可利用的化工产品价值为100元。该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?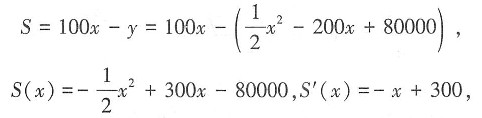
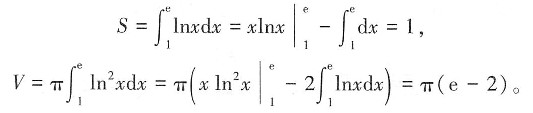
 (0,2),使得f(ξ)=0。
(0,2),使得f(ξ)=0。