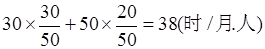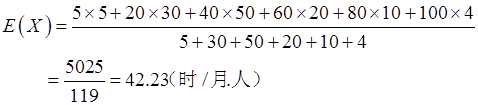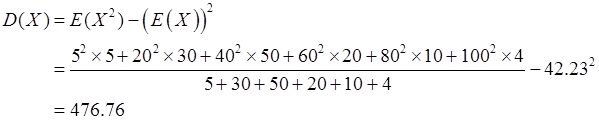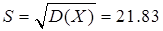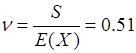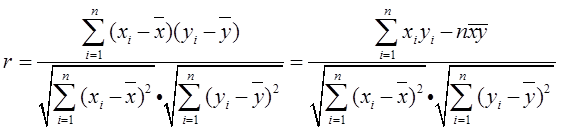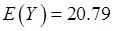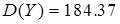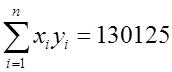一、单项选择题(在每小题给出的四个选项中,只有一个符合题目要求。) 三、计算与分析题(本大题共50分)1. 某商场服装的库存资料如下:

要求:计算该商场月平均库存。(保留整数)
时点指标是反映总体在某一特定时刻(瞬间)上的总量,商品库存是时点指标。某月平均库存量=(月初库存+月末库存)/2,本题中把下一个月的月初库存量当做上一个月的月末库存量。1月、2月的平均库存量为(208+210)/2=209,3、4、5、6月的平均库存量为(210+216)/2=213。在时间间隔不等的情况下,月平均库存的计算公式为:

即该商场月平均库存为220件。
2. 某企业近三年的实际产值分别为500万元、600万元、700万元,超额完成计划的百分比分别为5%、10%、15%,计算平均每年超额完成任务的百分比。(保留两位小数)
设近三年的计划完成量分别是a、b、c,实际产量为A、B、C,则有a(1+5%)=A=500;b(1+10%)=B=600;c(1+15%)=C=700。
由上可得:a=476.19,b=545.45,c=608.70。
故有平均每年超额完成任务的百分比为:
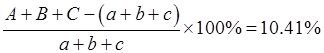
3. 甲、乙两个异地汽车经销商均出售某种汽车。根据记录,甲经销商该型号汽车的百辆月销量从参数为1的泊松分布,乙经销商该型号汽车的百辆月销量服从参数为2的泊松分布。两个经销商在同一个仓库提货。
问:该仓库每月应该准备多少辆汽车才能以不小于90%的概率保证顾客的需求。
泊松分布表 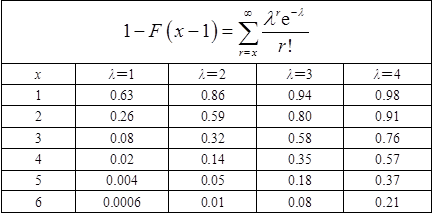
设X、Y分别表示甲乙两个经销商的销售数量,a表示满足要求时所需的库存量。则依题意有
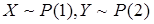
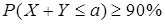
即

由泊松分布的可加性知:
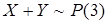
查泊松分布表可知,服从参数为3的泊松分布当x=6时,
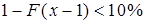
故库存量为a=x-1=5时满足要求。
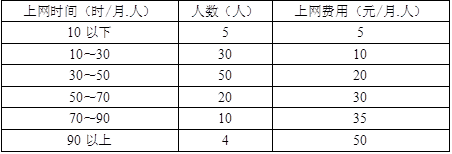
4. 计算该班学生上网时间的众数
上网时间的众数在组别30~50中,左右相邻组的频数(本题为上网人数)分别为30、20。
故由众数的的计算公式:众数=下组限
左相邻组的频数占左右相邻组总频数的百分比+上组限
右相邻组的频数占左右相邻组总频数的百分比。
可得众数为
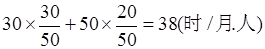
5. 计算该班学生上网时间的标准差及标准差系数
以组中值代表该组的平均水平,并设下开口组的组距为10,上开口组的组距为20,上网时间为X小时。则上网时间的均值为
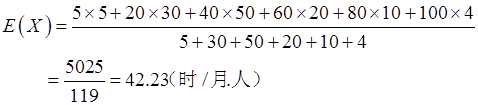
方差为
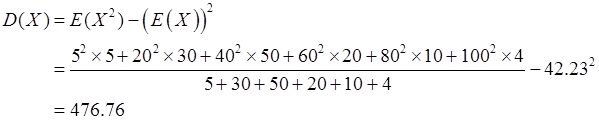
故标准差为
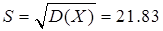
标准差系数为
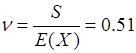
6. 计算每个学生上网时间和上网费用之间的相关系数
以组中值代表该组的平均水平,并设下开口组的组距为10,上开口组的组距为20,则上网时间为5,20,40,60,80,100(小时);设上网时间为X,上网费用为Y,则由相关系数的计算公式:
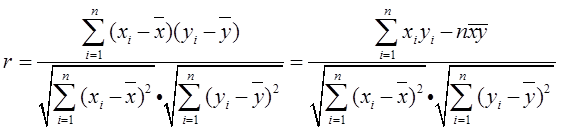
经计算得
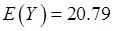
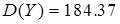
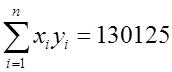
带入公式计算可得r=0.728。

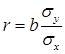
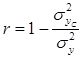
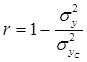
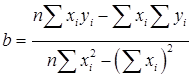
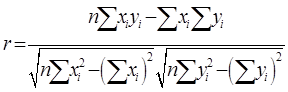
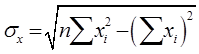
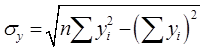
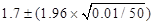
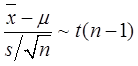
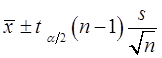
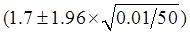
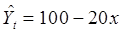
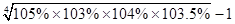
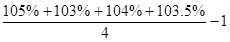
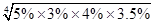
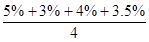
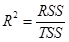
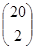 ,该事件包含的基本事件个数为
,该事件包含的基本事件个数为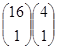 ,故概率为
,故概率为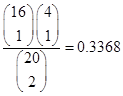
 的分布为______。
的分布为______。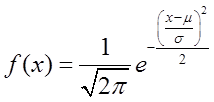
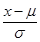 记为Y,则Y服从N(0,1)。
记为Y,则Y服从N(0,1)。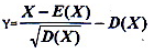
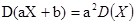
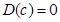
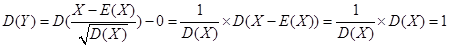
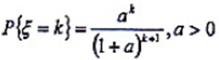 为常数,则ξ的期望是______。
为常数,则ξ的期望是______。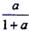

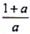
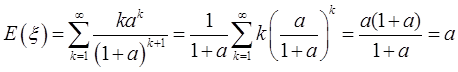
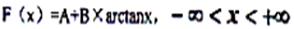
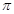
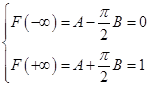
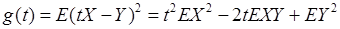
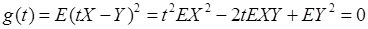
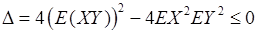
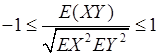
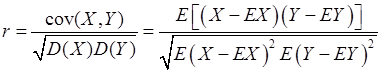
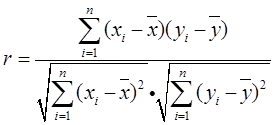
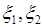 为两个试验,由其产生的基本事件空间(样本空间)分别是
为两个试验,由其产生的基本事件空间(样本空间)分别是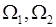 ,若对于任意的事件
,若对于任意的事件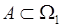 与任意的事件
与任意的事件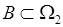 均有A事件与B事件相互独立,则称设
均有A事件与B事件相互独立,则称设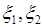 为两相互独立试验。
为两相互独立试验。

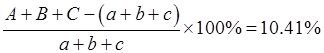
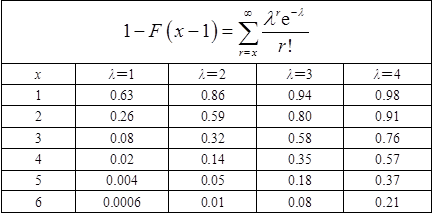
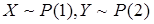
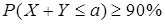

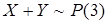
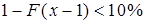
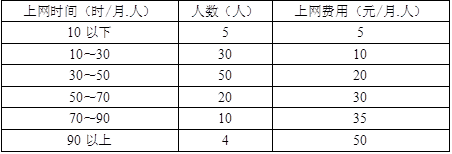
 左相邻组的频数占左右相邻组总频数的百分比+上组限
左相邻组的频数占左右相邻组总频数的百分比+上组限 右相邻组的频数占左右相邻组总频数的百分比。
右相邻组的频数占左右相邻组总频数的百分比。