一、选择题6. 已知F
1,F
2是椭圆
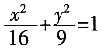
的两焦点,过点F
2的直线交椭圆于A,B两点。在△AF
1B中,若有两边之和是10,则第三边的长度为______。
A B C D
A
[解析] 根据椭圆定义,知△AF1B的周长为4a=16,故所求的第三边的长度为16-10=6。
7. 设等比数列{a
n}的前n项和为S
n,
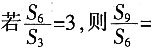
______。
A.2
B.
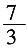
C.

D.3
A B C D
B
[解析] 设公比q,则
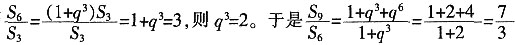
。
16. 若x
1,x
2是一元二次方程x
2+4x+3=0的两个根,则x
1x
2是______。
A B C D
B
[解析] 对于一元二次方程ax
2+bx+c=0(a≠0),若方程有两个实根x
1、x
2,则x
1+x
2=
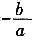
,x
1x
2=
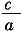
。由题意知x
1x
2=3。
17. 平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|=______。
A.
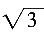
B.

C.4
D.12
A B C D
B
[解析] 由已知|a|=2,|a+2b|
2=a
2+4a·b+4b
2=4+4×2×1×cos60°+4=12,故|a+2b|=
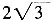
。
20. S
n为{a
n}前n项和,a
1=3,S
n+S
n+1=3a
n+1,则S
n=______。
- A.3n
- B.3n+1
- C.3×2n-1
- D.3×2n+1
A B C D
C
[解析] 因为S
n+S
n+1=3a
n+1 所以S
n+S
n+a
n+1=3a
n+1 S
n=a
n+1,S
n+1=2S
n S
1=a
1=3
S
2=2S
1=3×2
S
3=2S
2=3×2×2

所以S
n=3×2
n-1。
二、综合知识判断题3. 明知校舍或者教育教学设施有危险,而不采取措施,造成人员伤亡或者重大财产损失的,对直接负责的主管人员和其他直接责任人员,给予行政处分。
对 错
B
[解析] 明知校舍或者教育教学设施有危险,而不采取措施,造成人员伤亡或者重大财产损失的,对直接负责的主管人员和其他直接责任人员,依法追究刑事责任。
三、填空题1. 任取一个两位正整数N、对数log
2N是一个正整数的概率是______。
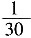
。
[解析] 两位正整数N可取10~99共90个数,log
2N为正整数,N可取16,32,64共3个数,故所求概率为
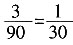
。
2. 设a>0,a≠1,则“函数f(x)=a
x在R上是减函数”是“函数g(x)=(2-a)x
3在R上是增函数”的______。
充分不必要条件。
[解析] p:“函数f(x)=ax在R上是减函数”等价于0<a<1;q:“函数g(x)=(2-a)x3在R上是增函数”等价于2-a>0,即0<a<2且a≠1,故p是q成立的充分不必要条件。
3. 已知抛物线y=x
2+2x+2,则该抛物线的顶点坐标是______。
4. 已知两个相似三角形的周长比是1:3,它们的面积比是______。
5. 已知正数x、y满足方程
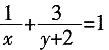
,则x+y的最小值是______。
[解析]
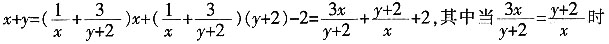
,该等式取得最小值为

。
6. 曲线y=x
3+x+1在点(1,3)处的切线方程是______。
4x-y-1=0
[解析] 由题意得即曲线y'=3x2+1,曲线y=x3+x+1在点(1,3)处切线的斜率为4,所以切线方程为y-3=4(x-1),即4x-y-1=0。
7. 两块一样重的合金,一块合金中铜与锌的比是3:7,另一块合金中铜与锌的比是2:3。现将两块合金合成一块,新合金中铜与锌的比是______。
8. 在Rt△ABC中,∠C=90°,sinA=
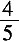
,则cosB的值等于______。
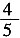
。
9. 在实数集内分解因式:a
4-1=______。
(a2+1)(a+1)(a-1)。
[解析] 利用平方差方式。
10. 6个大球与3个小球共重48克,6个小球与3个大球共重42克,则大球重______克。
6。
[解析] 由题意可知,9个大球与9个小球共重48+42=90克,则3个大球与3个小球共重90÷3=30克,所以1个大球重(48-30)÷3=6克。
四、解答题(共45分)1.
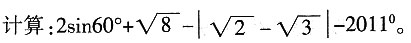
2. 二次函数的图象经过点(1,2)和(0,-1)且对称轴为x=2,求二次函数解析式。
设所求二次函数的解析式为:y=a(x-2)
2+k
由已知条件可得:
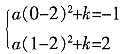
解得:
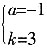
∴所求二次函数的解析式为:y=-(x-2)
2+3,
即y=-x
2+4x-1。
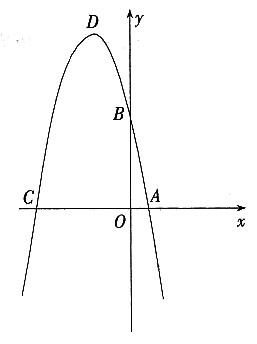
3. 如图,抛物线y=-x
2+bx+c与x轴的一个交点是A,与y轴的交点是B,且OA、OB(|OA<|OB|)的长是方程x
2-6x+5=0的两个实数根。
(1)求A、B两点的坐标;
(2)求出此抛物线的解析式及顶点D的坐标;
(3)求出此抛物线与x轴的另一个交点C的坐标;
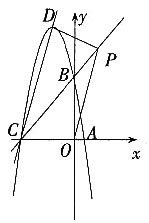
(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由。
(1)∵x
2-6x+5=0的两个实数根为x
1=1,x
2=5,
OA、OB(OA<OB)的长是方程x
2-6x+5=0的两个实数根,
∴OA=1,OB=5
∴A(1,0),B(0,5)。
(2)∵抛物线y=-x
2+bx+c与x轴的一个交点是A,与y轴的交点是B。
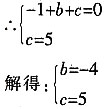
∴所求二次函数的解析式为:y=-x
24x+5。
顶点坐标为:D(-2,9)。
(3)此抛物线与x轴的另一个交点C的坐标为(-5,0)。
(4)直线CD的解析式为:y=3x+15,
直线BC的解析式为:y=x+5。
①若以CD为底,则OP∥CD,
直线OP的解析式为:y=3x。
于是有
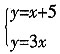
解得:
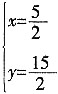
∴点P的坐标为
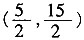
。
②若以OC为底,则DP∥CO。
直线DP的解析式为:y=9。
于是有

解得:
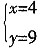
∴点P的坐标为(4,9)。
∴在直线BC上存在点P,使四边形PDCO为梯形且P点坐标为
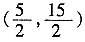
或(4,9)。
4. 已知:抛物线y=x
2+(b-1)x+c经过点P(-1,-2b)。
(1)求b+c的值;
(2)若b=3,求这条抛物线的顶点坐标;
(3)若b>3,过点P作直线PA⊥y轴,交y轴于点A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数关系式。
(1)依题意得:(-1)
2+(b-1)(-1)+c=-2b,
∴b+c=-2。
(2)当b=3时,c=-5,
y=x
2+2x-5=(x+1)
2-6,
抛物线的顶点坐标是(-1,-6)。
(3)当b>3时,抛物线对称轴x=
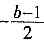
<-1,对称轴在点P的左侧。
因为抛物线是轴对称图形,P(-1,-2b)且BP=2PA。
∴B(-3,-2b)。
∴
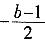
=-2,
∴b=5,
又b+c=-2,∴c=-7。
抛物线所对应的二次函数关系式y=x
2+4x-7。
5. 某中学要从甲、乙、内、]四名优秀学生中选2名去参加“全国中学生夏令营估动”,请你用画树状图(或列表)的方法,求出甲、乙两同学同时被选中的概率。
法1:树状图法
∴甲、乙两同学同时被选中的概率为
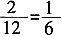
。
法2:列表法
|
|
甲
|
乙
|
丙
|
丁
|
| 甲
|
|
甲乙
|
甲丙
|
甲丁
|
| 乙
|
乙甲
|
|
乙丙
|
乙丁
|
| 丙
|
丙甲
|
丙乙
|
|
丙丁
|
| 丁
|
丁甲
|
丁乙
|
丁丙
|
|
∴甲、乙两同学同时被选中的概率为
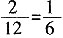
。
6. 已知:在Rt△ABC中,∠C=90°,∠A=2∠B,AB=6,求∠A,∠B的度数及边AC、BC的长。
∵∠C=90°
又∵∠A+∠B=90°
∴∠B=30°,∠A=60°,
∵sinA=
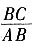
,
∴BC=AB·sinA=6sin60°=
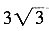
∵cosA=

,
∴AC=AB·cosA=6cos60°=3。
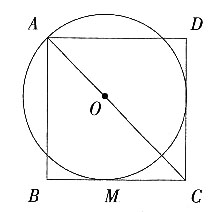
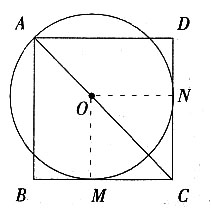
7. 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M。
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为1,求正方形ABCD的边长。
(1)过O作ON⊥CD于N,连结OM,则OM⊥BC。
∵AC是正方形ABCD的对角线,
∴AC是∠BCD的平分线。
∴OM=ON。
即圆心O到CD的距离等于⊙0半径,
∴CD与⊙O相切。
(2)由(1)易知△MOC为等腰直角三角形,OM为半径,
∴OM=MC=1
∴OC
2=OM
2+MC
2=1+1=2,
∴OC=
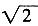
,
∴AC=AO+OC=1+
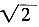
在Rt△ABC中,AB=BC,
由AC
2=AB
2+BC
2 ∴2AB
2=AC
2 ∴AB=
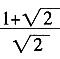
故正方形ABCD的边长为

。
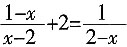 ,可知方程______。
,可知方程______。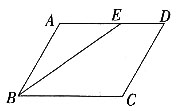

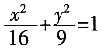 的两焦点,过点F2的直线交椭圆于A,B两点。在△AF1B中,若有两边之和是10,则第三边的长度为______。
的两焦点,过点F2的直线交椭圆于A,B两点。在△AF1B中,若有两边之和是10,则第三边的长度为______。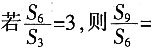 ______。
______。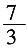

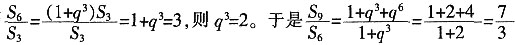 。
。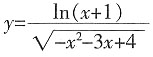 的定义域为______。
的定义域为______。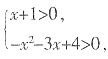 解得-1<x<1。
解得-1<x<1。
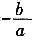 ,x1x2=
,x1x2=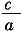 。由题意知x1x2=3。
。由题意知x1x2=3。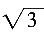

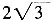 。
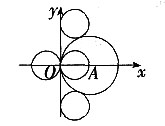
。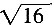 的算术平方根是______。
的算术平方根是______。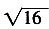 =4,4的算术平方根为2。
=4,4的算术平方根为2。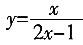 在点(1,1)处的切线方程为______。
在点(1,1)处的切线方程为______。
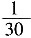 。
。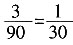 。
。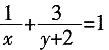 ,则x+y的最小值是______。
,则x+y的最小值是______。
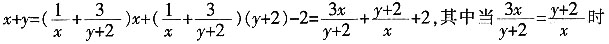 ,该等式取得最小值为
,该等式取得最小值为 。
。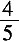 ,则cosB的值等于______。
,则cosB的值等于______。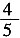 。
。

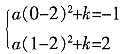
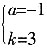
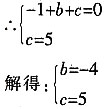
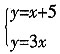 解得:
解得: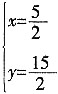
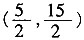 。
。 解得:
解得: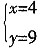
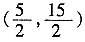 或(4,9)。
或(4,9)。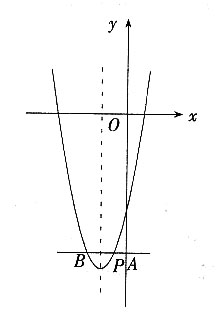
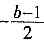 <-1,对称轴在点P的左侧。
<-1,对称轴在点P的左侧。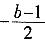 =-2,
=-2,
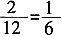 。
。
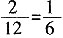 。
。
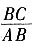 ,
,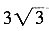
 ,
,
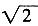 ,
,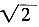
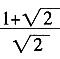
 。
。