论述题1. 在多电子的原子中,核外电子的排布应遵循哪些原则?
能量最低原理,Pauli不相容原理,Hund规则。
2. 试证明理想密排六方结构的轴比
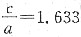
。
见下图,等边三角形的高
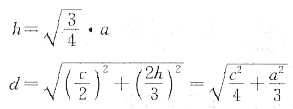
理想密排六方晶体结构中d=a,
故
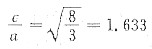
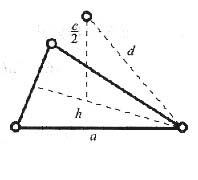
3. 试指出Cu和α-Fe两晶体易滑移的晶面和晶向,并求出他们的滑移面间距,滑移方向上的原子间及点阵阻力。(已知G
Cu=48.3GPa,G
α-Fe=81.6GPa,υ=0.3)。
Cu系fcc结构,其易滑移面为{111},易滑移方向为<110>。
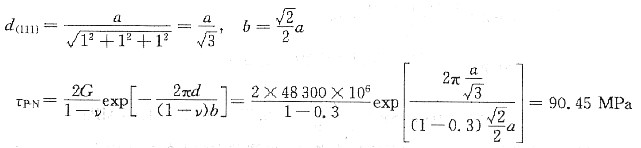
α-Fe系bcc结构,其滑移面为{110},易滑移方向为(111)。
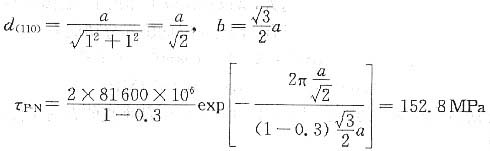
4. 设冷变形后位错密度为10
12/cm
2的金属中,存在着加热时不发生聚集长大的第二相微粒,其体积分数φ=1%,半径为1μm,问这种第二相微粒的存在能否完全阻止此金属加热时再结晶(已知G=10
5MPa,b=0.3nm,比界面能σ=0.5J/m
2)。
再结晶驱动力
F=Gb
2(ρ-ρ
0)≈Gb
2ρ=10
11×(3×10
-10)
2×10
16=9×10
7N/m
2 再结晶阻力
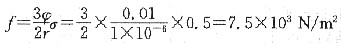
F>>f,故这种第二相微粒的存在不能完全阻止再结晶。
5. 一有机化合物,其组成的ω(C)为62.1%,ω(H)为10.3%,ω(O)为27.6%。试推断其化合物名称。
各组分的摩尔分数分别为:
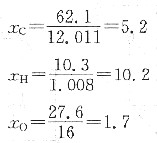
C:H:O=5.2:10.2:1.7≈3:6:1

故可能的化合物为CH
3COCH
3(丙酮)。
6. 在一个富碳的环境中对钢进行渗碳,可以硬化钢的表面。已知在1000℃下进行这种渗碳热处理,距离钢的表面1~2mm处,碳含量从x=5%减到x=4%。估计在近表面区域进入钢的碳原子的流入量J(原子数/(m
2·s))。(γ-Fe在1000℃的密度=7.63g/cm
3,碳在γ-Fe中的扩散系数D
0=2.0×10
-5m
2/s,激活能Q=142kJ/mol)。
首先,应把溶质碳原子的含量从原子分数转换为体积分数,故必须先求出溶剂铁原子的单位体积原子数,即
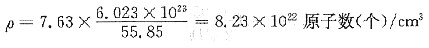
近似认为(碳原子数+铁原子数)=铁原子数,则有

根据菲克(Fick)第一定律:
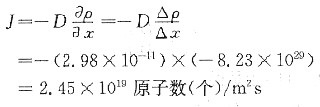
7. 分别解释柯氏气团(Cottrell atmosphere)和铃木气团(Suzuki atmosphere)在强化金属中的作用。
柯氏气团:BCC晶体(如碳钢)中,C、N等小尺寸原子优先分布于刃型位错的拉应力区,对位错产生钉扎作用。要使位错运动,必须从钉扎作用下撕脱出,需要增加额外的应力,从而提高了材料的强度。
铃木气团:FCC晶体(如不锈钢)中,Ni、Cr等合金元素优先分布于层错区,降低层错能,使扩展位错区扩大,要使该扩展位错运动,需要增加额外的应力,从而提高了材料的强度。
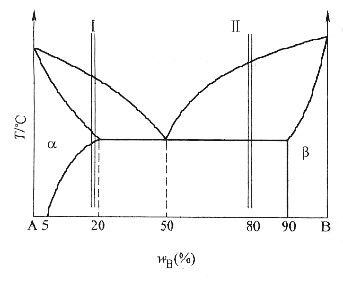
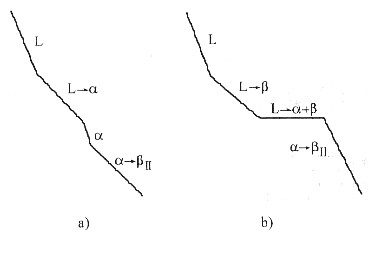
8. 分析合金Ⅰ、Ⅱ的平衡结晶过程,并绘出冷却曲线。
合金Ⅰ、Ⅱ的平衡结晶过程及冷却曲线分别如图3-11a和b所示。
9. 说明室温下Ⅰ、Ⅱ的相和组织是什么,并计算出相和组织的相对含量。
Ⅰ:α
初+β
Ⅱ,相组成与组织组成比例相同
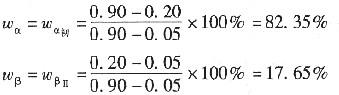
Ⅱ:β
初+ (α+β)
共,
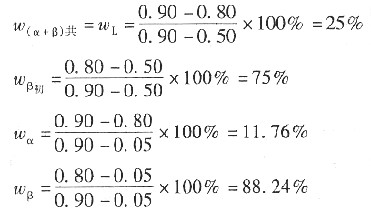
10. 如果希望得到共晶组织和5%的β
初的合金,求该合金的成分。
设所求合金成分为x
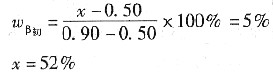
11. 分析在快速冷却条件下,Ⅰ、Ⅱ合金获得的组织有何不同。
Ⅰ合金在快冷条件下可能得到少量的共晶组织,且呈现离异共晶的形态,合金中的βⅡ量会减少,甚至不出现;Ⅱ合金在快冷条件下β初呈树枝状,且数量减少。共晶体组织变细小,相对量增加。