一、问题求解(在每小题的五个选项中选择一项)
6. 点A
1,A
2,A
3,…,A
n(n为正整数)都在数轴上.点A
1在原点O的左边,且A
1O=1;点A
2在点A
1的右边,且A
2A
1=2;点A
3在点A
2的左边,且A
3A
2=3;点A
4在点A
3的右边,且A
4A
3=4;…,依照上述规律,点A
2008,A
2009所表示的数分别为______
- A.2008,-2009
- B.-2008,2009
- C.1004,-1005
- D.1004,-1004
- E.2008,2009
A B C D E
C
[解析] 由题目可知:A2008是在原点右边的第1004个点处,所以为1004,A2009为原点左边的1005个点处,所以为-1005.
12. 若从1,2,3,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有______种.
A B C D E
D
[解析] 分以下三种情况:
(1)4个数全为奇数,有

种取法;
(2)4个数全为偶数,有

种取法;
(3)2个奇数和2个偶数,有

种取法.
则满足条件的取法共有

种.
综上所述,答案选择D.
二、条件充分性判断解题说明:本大题要求判断所给出的条件能否充分支持题干中陈述的结论.阅读条件(1)和(2)后选择.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和(2)联合起来也不充分.
1. 数列{a
n}是递增数列.
(1){a
n}是等比数列,a
1<a
2<a
3.
(2){a
n}是等差数列,a
1+a
3<a
2+a
4.
A B C D E
D
[解析] 对于条件(1),由{an}为等比数列,知an=a1qn-1,且a1<a2<a3,
可得a1<a1q<a1q2,即a1>0,q>1或a1<0,0<q<1,则数列{an}是递增数列.
故条件(1)充分.
对于条件(2),由{an}为等差数列,且a1+a3<a2+a4可得a1-a2<a4-a3,
即-d<d,d<0,则数列{an}是递增数列.故条件(2)充分.
综上所述,答案选择D.
3. 如图所示,在三角形ABC中,分别以AC,BC为边作正方形ACFG,BCED,则三角形CEF的面积是100.
(1)三角形ABC的面积是100.
(2)三角形ABC中:∠ACB=90°.
A B C D E
A
[解析] 三角形面积

由条件(1),

又AC=CF,BC=CE,∠ACB+∠ECF=180°,sin∠ECF=sin∠ACB,
所以S
△CEF=S
△ABC=100,条件(1)充分.
条件(2)无法推出结论,故条件(2)不充分.
综上所述,答案选择A.
5. a
1a
8<a
4a
5.
(1){a
n}为等差数列,且a
1>0.
(2){a
n}为等差数列,且公差d≠0.
A B C D E
B
[解析] a1a8-a4a5=a1(a1+7d)-(a1+3d)(a1+4d)=-12d2<0,
因此条件(1)不充分,条件(2)充分.综上所述,答案选择B.
6.

(1)将半径为R的球切割成一个长方体.则长方体的最大体积为a.
(2)将半径为R的球切割成一个圆柱体.则圆柱体的最大体积为a.
A B C D E
A
[解析] 对于条件(1),设长方体的长、宽、高分别为x,y,z,
则

当x=y=z时,xyz取最大值.
此时该长方体为正方体,则有

则条件(1)充分.
对于条件(2),设圆柱体的底面半径为r,高为h,
则加工为圆柱体体积最大时有4R
2=4r
2+h
2,

综上所述,答案选择A.
7. 甲、乙两人曾三次一同去买食盐,他们的买法不同.由于市场波动,三次食盐价格不相同.三次购买,甲购买的食盐平均价格要比乙低.
(1)甲每次购买一元钱的盐,乙每次购买1kg的盐.
(2)甲每次购买数量不等,乙每次购买数量恒定.
A B C D E
A
[解析] 设三次食盐价格分别为a,b,c元/kg,
由条件(1)甲的平均价格为

乙的平均价格为

由平均值不等式得甲的平均价格≤乙的平均价格(当a=b=c时取等号).
由条件(2)设甲每次购买m,n,pkg盐,甲的平均价格为

乙的平均价格为

取m=1,n=2,p=3,则甲的平均价格-乙的平均价格=

无法确定正负.
因此条件(1)充分,条件(2)不充分.
综上所述,答案选择A.
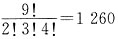 种排法.
种排法. 种;
种;
 (|x|-1)(|y|-1)=0
(|x|-1)(|y|-1)=0 |x|=1,|y|=1.表示边长为2的正方形,所以面积为4.
|x|=1,|y|=1.表示边长为2的正方形,所以面积为4.





 则小强今年16岁,叔叔今年28岁.
则小强今年16岁,叔叔今年28岁.




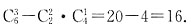
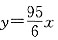
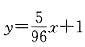
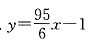
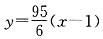
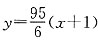
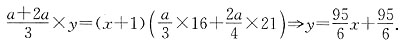

 种取法;
种取法; 种取法;
种取法; 种取法.
种取法. 种.
种. 解得
解得 即客轮的航速和水流速度分别为每小时27.5km和5.5km.
即客轮的航速和水流速度分别为每小时27.5km和5.5km.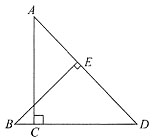
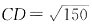 ,则
,则 ,于是
,于是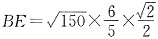 ,故△BDE的面积
,故△BDE的面积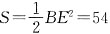 .
.





 当x=y=z时,xyz取最大值.
当x=y=z时,xyz取最大值. 则条件(1)充分.
则条件(1)充分.
 乙的平均价格为
乙的平均价格为 由平均值不等式得甲的平均价格≤乙的平均价格(当a=b=c时取等号).
由平均值不等式得甲的平均价格≤乙的平均价格(当a=b=c时取等号). 乙的平均价格为
乙的平均价格为 取m=1,n=2,p=3,则甲的平均价格-乙的平均价格=
取m=1,n=2,p=3,则甲的平均价格-乙的平均价格= 无法确定正负.
无法确定正负. ,则
,则



 联合解得
联合解得 故条件(1)充分.
故条件(1)充分.



 ,这3个数之和为M.
,这3个数之和为M. ,这3个数之和为M.
,这3个数之和为M. 可得7,8,9三个数满足条件,M=7+8+9=24成立,故条件(1)充分.
可得7,8,9三个数满足条件,M=7+8+9=24成立,故条件(1)充分. 可逐个验证三个数为2,7,11,则M=2+7+11=20,故条件(2)不充分.
可逐个验证三个数为2,7,11,则M=2+7+11=20,故条件(2)不充分.