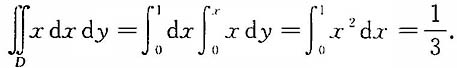银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
广东省专升本考试高等数学真题2019年
一、单项选择题
(每小题给出的四个选项，只有一项是符合题目要求的)
1. 函数
的间断点是______
A.x=-2和x=0
B.x=-2和x=1
C.x=-1和x=2
D.x=0和x=1
A
B
C
D
B
[解析] 因为
在x=-2和x=1处没有定义，
所以函数f(x)的间断点是x=-2和x=1．
2. 设函数
则
______
A.等于1
B.等于2
C.等于1或2
D.不存在
A
B
C
D
A
[解析] 因为
，所以
3. 已知∫f(x)dx=tanx+C，∫g(x)dx=2
x
+C，C为任意常数，则下列等式正确的是______
A．∫[f(x)g(x)]dx=2
x
tanx+C
B．
C．∫f[g(x)]dx=tan(2
x
)+C
D．∫[f(x)+g(x)]dx=tanx+2
x
+C
A
B
C
D
D
[解析] 由不定积分的可加性知，∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx=tanx+2
x
+C．
4. 下列级数收敛的是______
A．
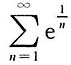
B．
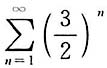
C．
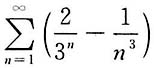
D．
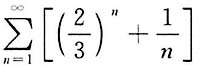
A
B
C
D
C
[解析] 因为
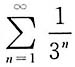
是公比为
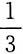
的等比级数，收敛；
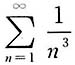
为p=3的p-级数，收敛，
所以级数
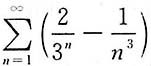
收敛．
5. 已知函数
在点x=-1处取得极大值，则常数a，b应满足条件______
A.a-b=0，b＜0
B.a-b=0，b＞0
C.a+b=0，b＜0
D.a+b=0，b＞0
A
B
C
D
B
[解析]
，因为f(x)在点x=-1处取得极大值，则
f'(-1)=a-b=0，f"(-1)=-2b＜0，即b＞0．
二、填空题
1. 曲线
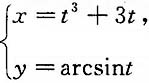
在t=0的对应点处的切线方程为y=______.
[解析] 当t=0时，x=0，y=0，切线斜率
=
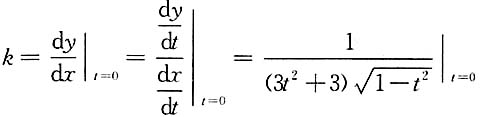
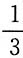
，所以切线方程为
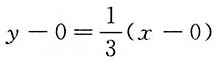
，即
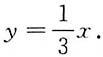
2. 微分方程ydx+xdy=0满足初始条件y|
x=1
=2的特解为y=______.
[解析] 方程分离变量得
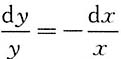
，两边积分得ln|y|=-ln|x|+C
1
，则xy=C，
又因为y|
x=1
=2，所以C=2，则特解为xy=2，即
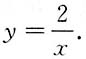
3. 若二元函数z=f(x，y)的全微分dz=e
x
sinydx+e
x
cosydy，则
=______.
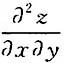
e
x
cosy
[解析] 由题意知，
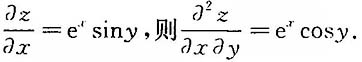
4. 设平面区域D={(x，y)|0≤y≤x，0≤x≤1}，则
=______.
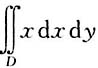
[解析]
5. 已知
，则
=______.
π
[解析]
三、计算题
(每小题6分，共48分)
1. 求
2. 设
，求
两边同时取对数，得
两边同时求导得
故
3. 求不定积分
4. 计算定积分
令
，则
，dx=tdt．当
时，t=0；当x=0时，t=1，故
5. 设x-z=e
xyz
，求
令F(x，y，z)=x-z-e
xyz
，则
F
x
=1-yze
xyz
，F
y
=-xze
xyz
，F
z
=-1-xye
xyz
，
当F
z
≠0时，有
6. 计算二重积分
，其中平面区域D={(x，y)|1≤x
2
+y
2
≤4}．
由被积函数及积分区域可知本题选用极坐标计算较为简便，令x=rcosθ，
y=rsinθ，则积分区域可表示为0≤θ≤2π，1≤r≤2，故
7. 已知级数
满足0≤a
n
＜b
n
，且
，判定级数
的收敛性．
因为b
n
＞0，所以
是正项级数，且
所以由比值审敛法可知级数
是收敛的，
又0≤a
n
＜b
n
，所以由比较审敛法可知级数
也是收敛的．
8. 设函数f(x)满足
，求曲线y=f(x)的凹凸区间．
由题意得df(x)=xde
-x
=-xe
-x
dx，即
f'(x)=-xe
-x
，f"(x)=(x-1)e
-x
，
f(x)在(-∞，+∞)上二阶可导，当x＞1时，f"(x)＞0；当x＜1时，f"(x)＜0．
故曲线y=f(x)的凹区间为(1，+∞)，凸区间为(-∞，1)．
四、综合题
(第1小题12分，第2小题10分，共22分)
已知连续函数φ(x)满足
1. 求φ(x)；
对等式
两边求导得，
对上式再求导得φ"(x)=-φ(x)，
令y=φ(x)，则y"+y=0，是二阶线性齐次微分方程，其对应的特征方程为r
2
+1=0，解得特征根为r
1
=i，r
2
=-i，
故方程通解为y=φ(x)=C
1
cosx+C
2
sinx，φ'(x)=-C
1
sinx+C
2
cosx．
又因为φ(0)=1，φ'(0)=1，所以C
1
=1，C
2
=1，
即φ(x)=cosx+sinx；
2. 求由曲线y=φ(x)和x=0，
及y=0围成的图形绕x轴旋转一周所得立体的体积．
所得立体的体积为
设函数f(x)=xln(1+x)-(1+x)lnx．
3. 证明：f(x)在区间(0，+∞)内单调减少；
由题意得
当x＞0时，f"(x)＞0，故f'(x)在(0，+∞)内单调递增，
则
，
因此可得f(x)在(0，+∞)内单调减少；
4. 比较数值2018
2019
与2019
2018
的大小，并说明理由.
由上小题可知，f(2018)＜f(3)=3ln4-4ln3=
＜ln1，因为
f(2018)=2018ln2019-2019ln2018
=ln2019
2018
-ln2018
2019
=
＜ln1，
所以
，即2019
2018
＜2018
2019
.
一、单项选择题
1
2
3
4
5
二、填空题
1
2
3
4
5
三、计算题
1
2
3
4
5
6
7
8
四、综合题
1
2
3
4
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
的间断点是______
在x=-2和x=1处没有定义，
则
______
，所以
是公比为
的等比级数，收敛；
为p=3的p-级数，收敛，
收敛．
在点x=-1处取得极大值，则常数a，b应满足条件______
，因为f(x)在点x=-1处取得极大值，则
在t=0的对应点处的切线方程为y=______.
=
，所以切线方程为
，即
，两边积分得ln|y|=-ln|x|+C1，则xy=C，
=______.
=______.
，则
=______.
，求
两边同时取对数，得
，则
，dx=tdt．当
时，t=0；当x=0时，t=1，故
，其中平面区域D={(x，y)|1≤x2+y2≤4}．
满足0≤an＜bn，且
，判定级数
的收敛性．
是正项级数，且
是收敛的，
也是收敛的．
，求曲线y=f(x)的凹凸区间．
两边求导得，
及y=0围成的图形绕x轴旋转一周所得立体的体积．
，
＜ln1，因为
＜ln1，
，即20192018＜20182019.
深色：已答题 浅色：未答题