一、单项选择题(每小题只有一项符合题目要求)1. 若当x→0时，(1+x
2)
a-1与1-cosx为等价无穷小，则a=______
A．0
B．
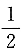
C．1
D．2
A B C D
B
[解析] 因为当x→0时，(1+x
2)
a-1与1-cosx为等价无穷小，所以
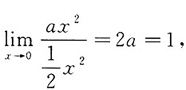
则
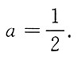
2. 设函数f(x)具有四阶导数，且
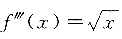
，则f
(4)(x)=______
A．
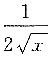
B．
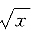
C．1
D．
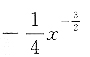
A B C D
A
[解析] 因为
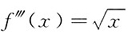
，所以
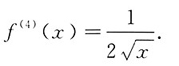
3. 设函数f(x)的一个原函数为ln2x+1，则∫f
'(2x)dx=______
A．ln2x+C
B．
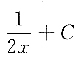
C．
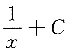
D．
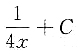
A B C D
D
[解析] 因为
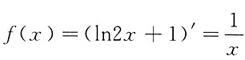
，所以
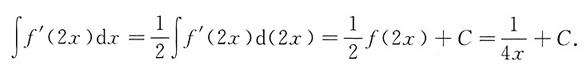
4. 函数z=f(x，y)在点(x
0，y
0)处的两个偏导数
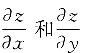
存在，则它在点(x
0，y
0)处______
A B C D
C
[解析] 偏导数存在不一定连续，只有存在连续的偏导数时，函数可微，进而连续，故选C．
5. 下列无穷级数收敛的是______
A．
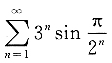
B．
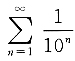
C．
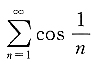
D．
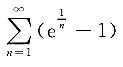
A B C D
B
[解析] A项中，
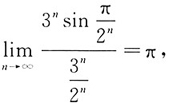
由比较审敛法的极限形式可知
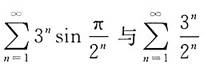
的敛散性相同，都是发散的；B项中，级数
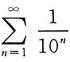
为公比
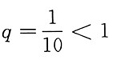
的等比级数，收敛；C项中，
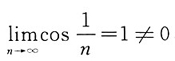
，因此
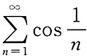
发散；D项中，由于当n→∞时，
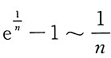
，而
发散，因此由比较审敛法的极限形式知级数
发散．
二、填空题1. 函数
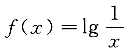
的连续区间为______．
(0，+∞)
[解析] 函数有意义需满足
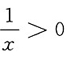
，即定义域为x＞0．因为初等函数在定义区间上是连续的，所以f(x)的连续区间为(0，+∞)．
2. 函数
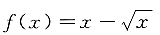
的单调减少区间是______．
[解析] 由题意可知，f(x)的定义域为[0，+∞)，
，令f
'(x)＜0，即
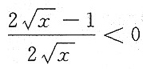
，解之得
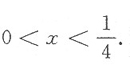
3. 反常积分
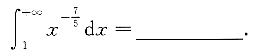
[解析]
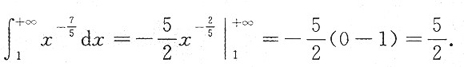
4. 微分方程
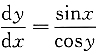
的通解是______．
siny+cosx=C
[解析] 方程分离变量可得cosydy=sinxdx，两边积分得siny=-cosx+C，即
siny+cosx=C．
5. 设平面区域D由直线y=x，y=-x及y=1所围成，则二重积分
．
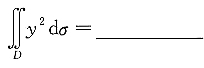
[解析] 由题意可知积分区域可表示为0≤y≤1，-y≤x≤y，故
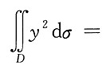
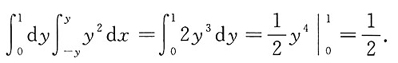
四、综合题(本大题共22分)1. 设平面x=1，x=-1，y=1和y=-1围成的柱体被坐标平面z=0和平面x+y+z=3所截，求截得的立体的体积．
由于所截得的立体是一个曲顶柱体，其曲顶为z=3-x-y，而其底为区域D：
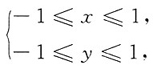
因此截得的立体的体积
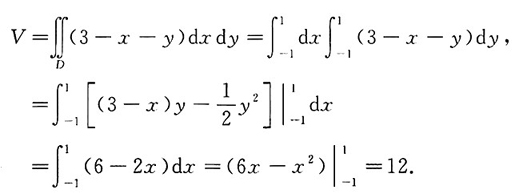
2. 常数a，b的值．
f(x)=ax
4+bx
3，f
'(x)=4ax
3+3bx
2，
因为f(x)在x=3处取得极值-27，所以f(3)=-27，f
'(3)=0，
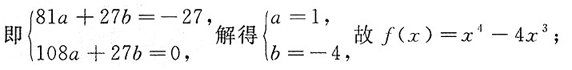
3. 曲线y=f(x)的凹凸区间与拐点．
f(x)的定义域为(-∞，+∞)，且f
'(x)=4x
3-12x
2，f
"(x)=12x
2-24x，令f
"(x)=0，得x
1=0，x
2=2．
列表得
所以曲线y=f(x)的凹区间为(-∞，0)和(2，+∞)，凸区间为(0，2)，拐点为(0，0)，(2，-16)．
确定函数y=y(x)，求
代入y，y'可得
的收敛性．
发散．
深色：已答题 浅色：未答题