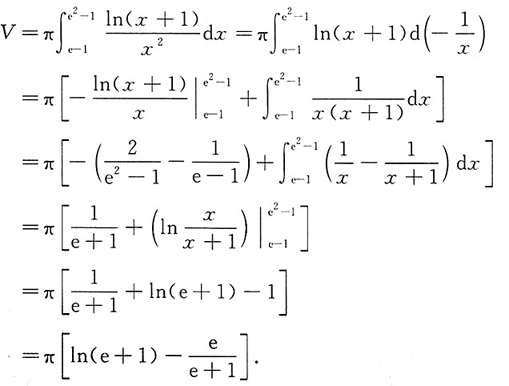银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
广东省专升本考试高等数学模拟7
一、单项选择题
(每小题只有一项符合题目要求)
1. 下列极限不存在的是______
A．
B．
C．
D．
A
B
C
D
A
[解析]
，极限不存在．
2. 如果f(x)的一个原函数为x-arcsinx，则∫f(x)dx=______
A．x+arcsinx+C
B．
C．x-arcsinx+C
D．
A
B
C
D
C
[解析] 由题意知∫f(x)dx=x-arcsinx+C．
3. 当x→0时，
是1-cosx的______
A.低阶无穷小
B.高阶无穷小
C.等价无穷小
D.同阶但不等价无穷小
A
B
C
D
C
[解析]
，即x→0时，
是1-cosx的等价无穷小，故选C．
4. 设区域D为x
2
+y
2
≤9，则
______
A.0
B.2
C.6
D.9
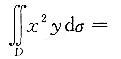
A
B
C
D
A
[解析] 因为积分区域关于x，y轴都对称，且被积函数x
2
y是关于y的奇函数，所以
．
5. 已知点P在曲线
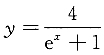
上，α为曲线在点P处的切线的倾斜角，则α的取值范围是______
A．
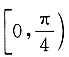
B．
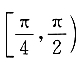
C．
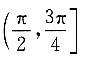
D．
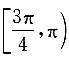
A
B
C
D
D
[解析]
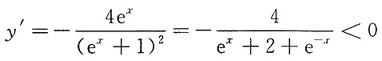
，又因为
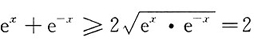
，所以1≤y
'
＜0，故1≤tanα＜0，解得
，故选D．
二、填空题
1. 设
有可去间断点x=1，则a=______．
1
[解析] 由于
有可去间断点x=1．故极限
存在，又
，故
，则a=1．
2. 定积分
[解析]
故
3. 微分方程
的通解为______．
ln
2
y=x
2
+C
[解析] 方程分离变量可得
，两边积分得
即ln
2
y=x
2
+C．
4. 设函数
，则
[解析]
5. 若
，则
2a
1
-S
[解析] 因为
，所以
三、计算题
(每小题6分，共48分)
1. 求极限
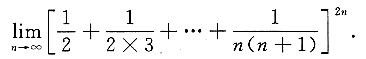
2. 若函数f(x)=(lnx)
x
(x＞1)，求f
'
(x)．
f(x)=(lnx)
x
=e
xln(lnx)
，则
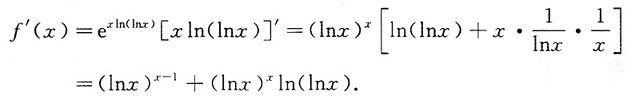
3. 求不定积分
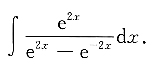
4. 计算定积分
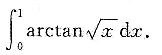
设
，则x=t
2
，当x=0时，t=0，当x=1时，t=1．于是
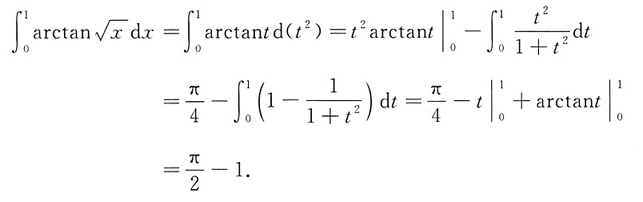
5. 设z=f(x，y)是由方程2xz-2xyz+ln(xyz)=0确定的隐函数，计算
设F(x，y，z)=2xz-2xyz+ln(xyz)．
则
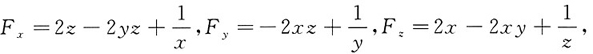
当F
z
≠0时，
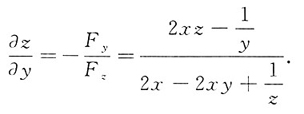
6. 计算二重积分
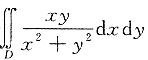
，其中区域D是由曲线
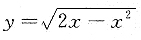
与直线y=x围成的闭区域．
积分区域如下图所示，则积分区域在极坐标系下可以表示为
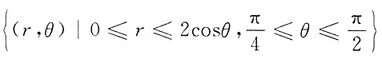
．所以
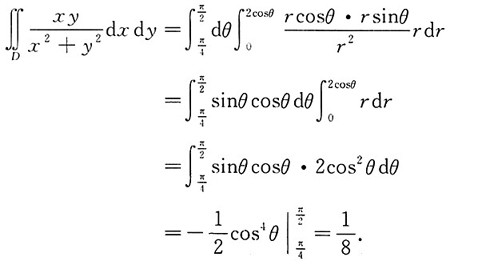
7. 求微分方程y
"
+25y=0满足初始条件y(0)=和y
'
(0)=-5的特解．
微分方程对应的特征方程为r
2
+25=0，解得特征根为r
1，2
=±5i，因此所给方程的通解为
y=C
1
cos5x+C
2
cos5x，
对上式求导，得y
'
=-5C
1
sin5x+5C
2
cos5x．
将初始条件y(0)=4，y
'
(0)=-5代入y，y
'
，得
解方程组，得C
1
=4，C
2
=-1．
于是所求特解为y=4cos5x-sin5x．
8. 判定级数
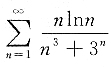
的收敛性．
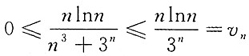
，对于级数
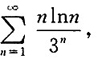
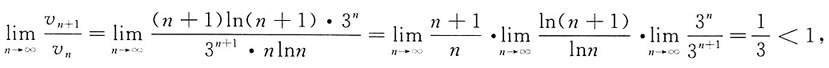
所以由比值审敛法知级数
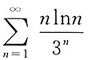
收敛，又由比较审敛法可知
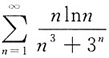
收敛．
四、综合题
(本大题共22分)
1. 已知某工厂生产x件产品的成本为
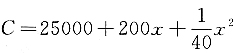
，产品的售价为每件500元，假设生产的产品能全部售出，要使利润最大，应该生产多少件产品?最大利润是多少?
利润函数
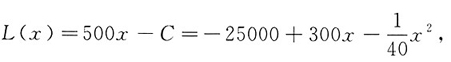
则
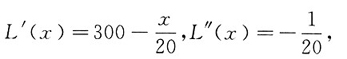
令L
'
(x)=0，得x=6000，
又
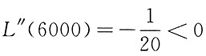
，故x=6000是极大值点，由于实际问题一定存在最值，且驻点唯一，故x=6000也为最大值点．
故要使利润最大，应该生产6000件产品，此时最大利润L(5000)=875000(元)．
设函数
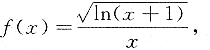
2. 求曲线y=f(x)的水平渐近线方程．
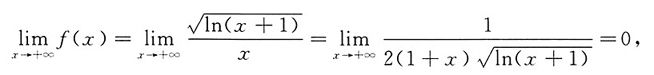
所以曲线的水平渐近线是y=0．
3. 求由曲线y=f(x)和直线x=e-1，x=e
2
-1及x轴所围平面图形绕x轴旋转一周所得旋转体的体积．
当x∈(e-1，e
2
-1)时，f(x)＞0，故所求旋转体的体积为
一、单项选择题
1
2
3
4
5
二、填空题
1
2
3
4
5
三、计算题
1
2
3
4
5
6
7
8
四、综合题
1
2
3
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
，极限不存在．
是1-cosx的______
，即x→0时，
是1-cosx的等价无穷小，故选C．
______
．
上，α为曲线在点P处的切线的倾斜角，则α的取值范围是______
，又因为
，所以1≤y'＜0，故1≤tanα＜0，解得
，故选D．
有可去间断点x=1，则a=______．
有可去间断点x=1．故极限
存在，又
，故
，则a=1．
故
的通解为______．
，两边积分得
即ln2y=x2+C．
，则
，则
，所以
，则x=t2，当x=0时，t=0，当x=1时，t=1．于是
，其中区域D是由曲线
与直线y=x围成的闭区域．
．所以
的收敛性．
，对于级数
收敛，又由比较审敛法可知
收敛．
，产品的售价为每件500元，假设生产的产品能全部售出，要使利润最大，应该生产多少件产品?最大利润是多少?
，故x=6000是极大值点，由于实际问题一定存在最值，且驻点唯一，故x=6000也为最大值点．
深色：已答题 浅色：未答题