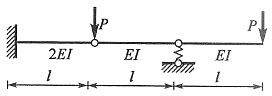
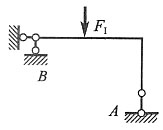
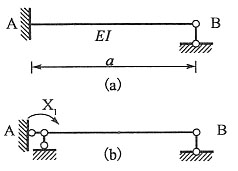
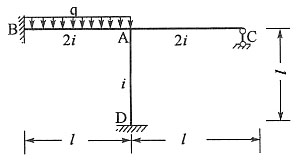
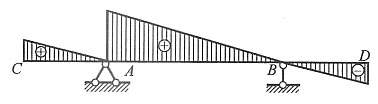
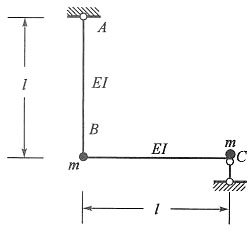
单项选择题28. 图示体系的自振频率为:______
A.
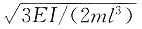
B.
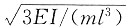
C.
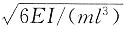
D.
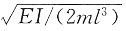
无
[解析] 图示结构为简支静定刚架,单自由度振动体系,M=2m,由图乘法可得水平向位移为
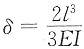
,可得体系自振频率为
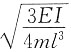
。
32. 一矩形混凝土梁b×h=250mm×600mm,h
0=530mm,混凝土C30(f
c=14.3MPa),主筋采用HRB400级钢筋(f
y=360MPa,ξ
b=0.518),按单筋计算时,此梁纵向受拉钢筋面积最大值为:______
- A.As,max=2317mm2
- B.As,max=2431mm2
- C.As,max=2586mm2
- D.As,max=2620mm2
A B C D
A
[解析] 为达到受拉钢筋截面面积最大,且不应超筋,即:
ξ=0.85ξ
b=0.85×0.518=0.44
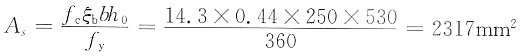
33. 矩形混凝土梁b×h=250mm×600mm,a
s=a'
s=40mm,混凝土C30(f
c=14.3MPa),主筋采用HRB335级钢筋(f
y=f'
y=300MPa,ξ
b=0.55),采用双筋截面,受拉筋A
s为
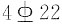
,受拉筋A'
s为
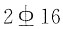
,K=1.2,试确定该梁所能承受的设计弯矩M是多少?______
- A.166.5kN·m
- B.170.3kN·m
- C.180.5kN·m
- D.195.6kN·m
A B C D
D
[解析] 根据SL 191—2008双筋矩形截面正截面受弯承载力计算公式:
f
cbx=f
yA
s-f'
yA'
s 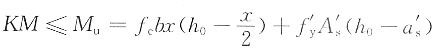
h
0=h-a
s=600-40=560mm
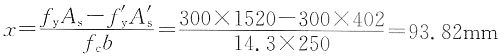
x<0.85ξ
bh
0=0.85×0.55×560=261.8mm
且
x>2a'
s=2×40=80mm
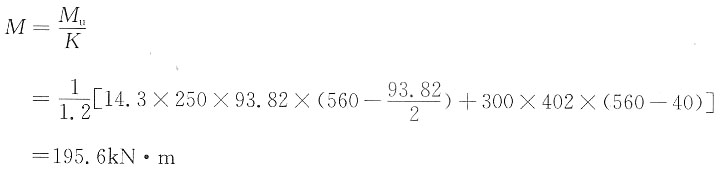
34. 已知一矩形混凝土梁,如图所示,箍筋采用HRB335(f
y=300MPa),箍筋直径为
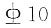
,混凝土C30(f
c=14.3MPa,f
t=1.43MPa),a
s=40mm,K=1.2,V=300kN,试确定该梁的箍筋间距s是多少?______
- A.100mm
- B.125mm
- C.150mm
- D.175mm
A B C D
C
[解析] 验算截面尺寸:
0.25f
cbh
0=0.25×14.3×250×560
=500.5kN>KV=1.2×300=360kN
截面尺寸满足要求。
验算是否按计算配箍:
V
c=0.7f
1bh
0 =0.7×1.43×250×560
=140.14kN<KV=1.2×300=360kN
需要按计算配箍。
由
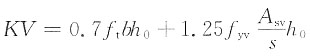
,带入数据得:
1.2×300×10
3=0.7×1.43×250×560+1.25×300×
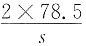
×560
算得s=150mm
37. 已知柱截面尺寸b×h=600mm×600mm,混凝土C60(f
c=27.5MP,f
t=2.04MPa),主筋采用HRB400级钢筋(f
y=f'
y=360MPa),ξ
b=0.518、a
s=a'
s=40mm,η=1.04,柱承受设计内力组合为M=±800kN·m(正反向弯矩),N=3000kN(压力),K=1.2,此柱配筋与下列值哪个最接近?______
- A.As=A's=1655mm2
- B.As=A's=1860mm2
- C.As=A's=1960mm2
- D.As=A's=2050mm2
A B C D
A
[解析] 判别大小偏心受压,由于采用对称配筋,故可按下式计算截面受压区高度:
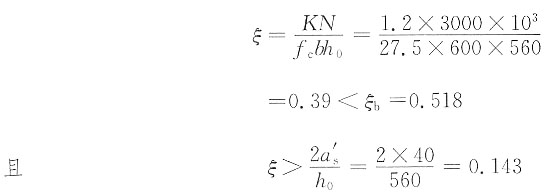
故属于大偏心受压构件。按矩形截面大偏心受压构件正截面受压承载力的基本公式,计算纵向受力钢筋截面面积:
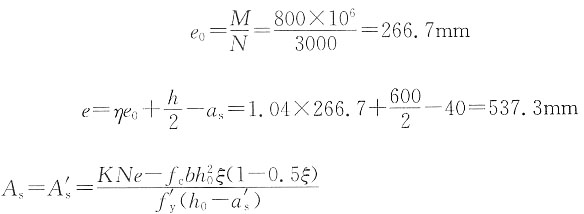
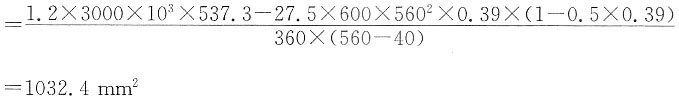
原题所给的4个选项有问题,只有选项A与题解结果最接近,符合原题“此柱配筋与下列值哪个最接近”的要求。按题意,原题有“M=±800kN·m(正反向弯矩)”的提示,且选项中有“A
s=A'
s”的提示,故只能采用对称配筋,而按对称配筋进行计算的正确答案只能是“1032mm
2”左右。
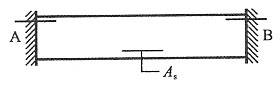
40. 两端嵌固的梁,承受均布荷载作用,跨中正弯矩配筋为A
s,支座A、B端的负弯矩配筋
分为三种情况:(1)2A
s;(2)A
s;(3)0.5A
s。以下哪种说法是正确的?______
- A.第(1)、(2)种情况可以产生塑性内力重分配,第(3)种情况下承载力最小
- B.第(2)、(3)种情况可以产生塑性内力重分配,第(3)种情况在A、B支座最先出现塑性铰,第(2)种情况支座出现塑性铰晚于第(3)种情况,第(1)种情况支座出现塑性铰时梁即告破坏,不存在塑性内力重分配
- C.第(2)、(3)种情况可以产生塑性内力重分配,第(2)种情况在支座处最先出现塑性铰
- D.第(1)、(2)、(3)种情况都可以产生塑性内力重分配,第(3)种情况在支座最先出现塑性铰,然后第(2)种情况支座产生塑性铰,最后第(1)种情况支座产生塑性铰
A B C D
B
[解析] 梁端嵌固的梁,在均布荷载q作用下,支座处产生
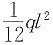
的负弯矩,跨中产生
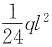
的正弯矩。可见支座处的弯矩为跨中的2倍。
(1)支座A、B端的负弯矩配筋2A
s时,恰好为跨中配筋的2倍,极限状态下,支座和跨中同时出现塑性铰,即告破坏,不存在内力重分布。
(2)支座A、B端的负弯矩配筋A
s时,极限状态下,支座A、B先出现塑性铰,存在内力重分布。
(3)支座A、B端的负弯矩配筋0.5A
s时,极限状态下,支座A、B先出现塑性铰,存在内力重分布,并且比(2)塑性铰出现的时间早。
故B项正确。
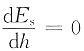 ,断面比能最小,弗劳德数Fr=1,水流为临界流。
,断面比能最小,弗劳德数Fr=1,水流为临界流。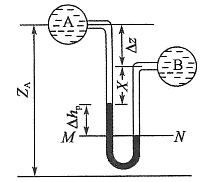
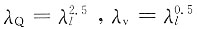 ,带入数据计算,得结果为D项。
,带入数据计算,得结果为D项。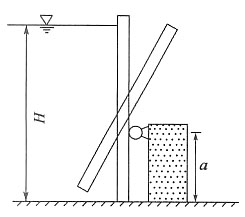
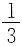 处,即为转轴高度,因此选B。
处,即为转轴高度,因此选B。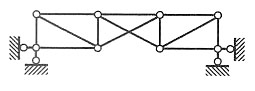
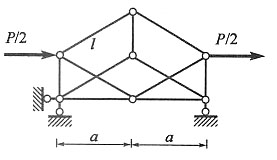
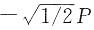
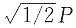
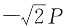




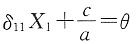
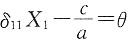
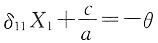
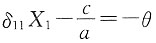
 。
。
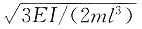
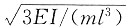
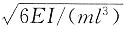
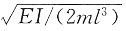
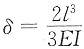 ,可得体系自振频率为
,可得体系自振频率为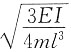 。
。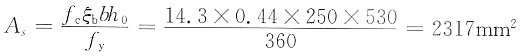
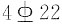 ,受拉筋A's为
,受拉筋A's为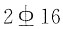 ,K=1.2,试确定该梁所能承受的设计弯矩M是多少?______
,K=1.2,试确定该梁所能承受的设计弯矩M是多少?______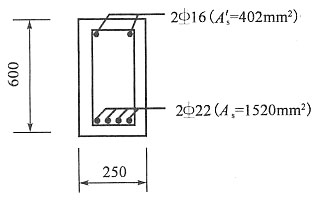
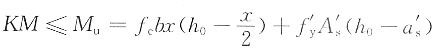
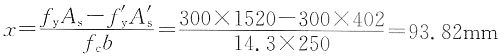
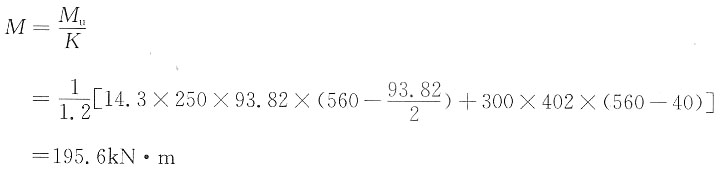
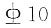 ,混凝土C30(fc=14.3MPa,ft=1.43MPa),as=40mm,K=1.2,V=300kN,试确定该梁的箍筋间距s是多少?______
,混凝土C30(fc=14.3MPa,ft=1.43MPa),as=40mm,K=1.2,V=300kN,试确定该梁的箍筋间距s是多少?______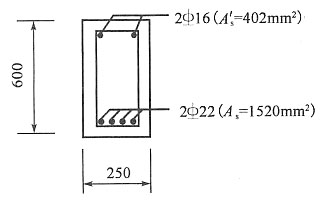
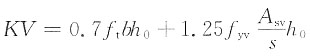 ,带入数据得:
,带入数据得: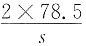 ×560
×560
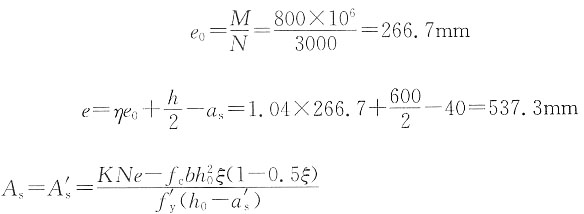
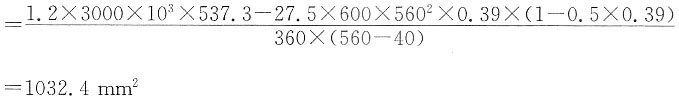
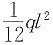 的负弯矩,跨中产生
的负弯矩,跨中产生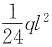 的正弯矩。可见支座处的弯矩为跨中的2倍。
的正弯矩。可见支座处的弯矩为跨中的2倍。