二、解答题1. 某饱和土样,测得含水量为31%,密度为1.95g/cm
3,试确定其相对密度、孔隙比、干重度。
设V=1cm
3 m=m
s+m
w=m
s(1+ω)=V·p=1.95g
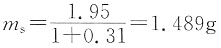
m
w=m-m
s=1.95-1.489=0.461g
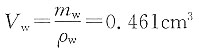
V
s=V-V
w=1-0.46=0.539
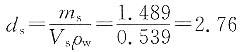
饱和土样,V
v=V
w 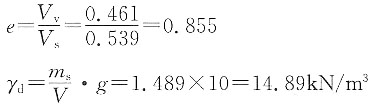
2. 某土样天然含水量34.5%,液限42%,塑限15%,试确定其塑性指数、液性指数、稠度状态。
I
p=ω
L-ω
p=42-15=27

为可塑状态。
3. 某砂土样天然孔隙比0.79,最大孔隙比0.95,最小孔隙比0.74,试确定其密实度。
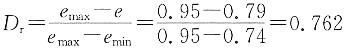
,为密实状态。
4. 某土样d
60=8.6mm,d
10=0.2mm,d
30=0.33mm,试确定其级配是否良好?
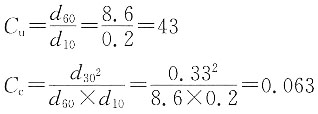
C
c<1,说明有粒径缺少现象,级配不良。
5. 某地基土层为两层,第一层为粉土,重度为18.5kN/m
3,厚度3.5m;第二层为砂土,饱和重度为20.5kN/m
3。地下水位位于第二层层顶,试计算6.8m处的自重应力。若地下水位下降至8.8m,6.8m处的自重应力变为多少?(第二层失水后天然重度为16.9kN/m
3)
地下水下降前:
σcz=γ1h1+γ'2h2=18.5×3.5+(20.5-10)×3.3=99.4kPa
地下水下降后:
σcz=γ1h1+γ2h2=18.5×3.5+16.9×3.3=120.52kPa
6. 某条形基础宽3.6m,地表以上荷载作用在距边缘1.4m处,大小为400kN/m,基础埋深1m,土层天然重度为16.9kN/m
3,试计算基底附加应力分布,并计算基础两个边缘下1.8m处的附加应力。
e=3.6/2-1.4=0.4m<3.6/6=0.6m,基底压力为梯形分布
F+G=400+3.6×1×1×20=472kPa
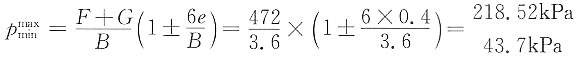
基底附加应力:p
0=p-γ·d
p
0min=26.80kPa,p
0max=201.62kPa
p
n=26.80kPa,p
t=201.62-26.80=174.82kPa
均布荷载下,基础两侧边缘下竖向应力相同,x/b=0,z/b=1.8/3.6=0.5,查表知,
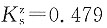
三角形分布荷载下,荷载偏向边缘下,x/b=1,z/b=0.5,查表知,
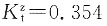
荷载偏离边缘下,x/b=0,z/b=0.5,查表知,

荷载偏向边缘下,附加应力为σ
z=0.479×26.80+0.354×174.82=74.72kPa
荷载偏离边缘下,附加应力为σ
z=0.479×26.80+0.125×174.82=34.69kPa
7. 矩形基础长6m,宽3.6m,其上作用200kPa的均布荷载,计算长边中点1.2m处的附加应力。
分为两个矩形:L/B=3.6/3=1.2,Z/B=1.2/3=0.4
查表知附加应力系数αc=0.242
附加应力:σz一αcp0×2=0.242×200×2=96.8kPa
8. 海底之下3m处取得某土样的先期固结压力为35kPa,海水深2m,土体饱和重度为20.5kN/m
3,试判断该土样的超固结性。
p0=γ'h=(20.5-10)×3=31.5kPa,而pc=35kPa,p0<pc,土为超固结土。
9. 某地基土体厚度4.5m,上下均为砂层。土的压缩系数a=0.60MPa
-1,初始孔隙比e=1.2,渗透系数k=2.5×10
-8cm/s,均布荷载p=180kPa,试计算加荷6个月后的沉降量。

双面排水,最大排水距离为层厚的一半,H=2.25m

由图中的曲线a=1,得相应的固结度U
t=61%,则S
t=S·U
t=0.135m
10. 某土样抗剪强度指标c=28kPa,φ=30°。土中某点应力为σ
z=250kPa,σ
x=100kPa,τ
zx=85kPa,试判断该点的应力稳定性。

σ
1>σ
1f,说明土体应力莫尔圆与抗剪强度线相割,土体已剪切破坏。
11. 某黄土地基各层的自重湿陷参数为:第一层,厚度2m,δ
sz1=0.018,第二层,厚度3m,δ
sz2=0.012,第三层,厚度2m,δ
sz3=0.016,试评价场地的自重湿陷性。
第二层,δsz2<0.015,不计入自重湿陷量计算
△zs=δsz1·h1+δsz3·3=0.018×2×100+0.016×2×100=6.8cm<7cm地基为非自重湿陷性场地。
12. 挡土墙墙高5m,墙背直立光滑,填土表面水平,填土c=10kPa,φ=20°,g=19kN/m
3,计算作用在挡土墙上的主动土压力与被动土压力。
采用朗肯土压力理论计算。
主动土压力:

墙底处:
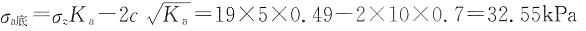
总主动土压力:
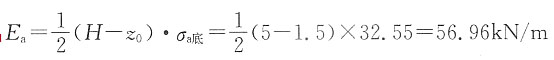
被动土压力:

墙顶处:

墙底处:

总被动土压力:

14. 利用极限荷载确定地基承载力,地基的破坏区有哪几个?
15. 有一条形基础宽b=2m,埋深d=1.0m,场地土层依次为填土,厚1.0m,重度γ=17kN/m
3,c=6kN/m
2,φ=15°;黏土,厚4.0m,重度γ=18kN/m
3,γ
sat=20kN/m
3,φ=26°,c=10kN/m
2;粉质砂土,未钻穿地下水位埋深1.0m。试计算地基的极限荷载(太沙基公式)和临界荷载
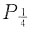
。
| φ | Nc | Nq | Nγ |
| 15° | 12.9 | 4.45 | 1.80 |
| 26° | 22.25 | 11.85 | 12.54 |
| |
| φ | Nc | Nq | 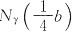 |
| 15° | 4.85 | 2.30 | 0.325 |
| 26° | 6.9 | 4.37 | 1.10 |
由(φ=26°,查表得,太沙基公式地基承载力系数:
N
c=22.25,N
q=11.85,N
γ=12.54
地形水位以下取有效重度,则:
p
u=γN
γ6/2+fN
x+qN
q =2×10×12.54/2+10×22.25+17×1×11.85=549.35kPa
由φ=26°,查表得,极限平衡区发展范围地基承载力系数:
N
c=6.9,N
q=4.37,Nγ=1.10
地形水位以下取有效重度,则:
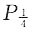
=γNγb+cN
c+qN
q =2×10×1.10+6.9×10+17×1×4.37=165.29kPa
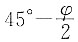 。
。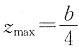 时,地基承载力应选择______。
时,地基承载力应选择______。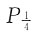
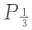
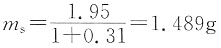
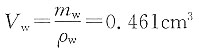
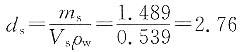
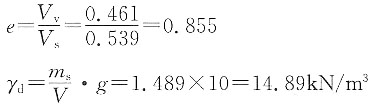

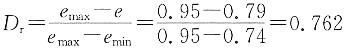 ,为密实状态。
,为密实状态。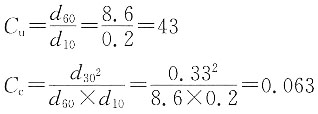
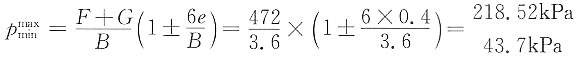
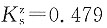
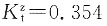





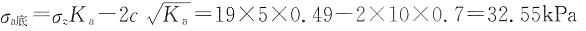
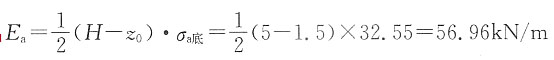




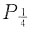 。
。 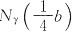
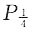 =γNγb+cNc+qNq
=γNγb+cNc+qNq