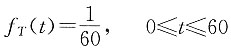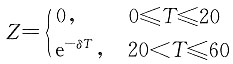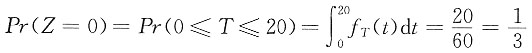计算题1. 下列哪些函数表达式可以作为生存函数?
(1)S(x)=exp[x-0.7(2
x-1)],x≥0
(2)

(3)S(x)=exp(-x
2),x≥0
解 作为生存函数的基本属性有:S(0)=1,函数是单调递减的,同时
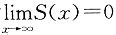
。
(1)由于S'(x)=exp[x-0.7(2
x-1)](1-0.7×2
x×ln2),S'(0)=0.5148>0,说明该函数不满足单调递减的性质。所以,它不能作为生存函数。
(2)由于
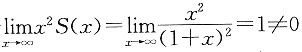
。该函数不可以作为生存函数。
(3)由于S(0)=1,S'(x)=(e
-x2)(-2x)<0,
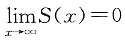
。该函数可以作为生存函数。
2. 如果
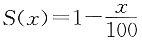
(0≤x≤100),请写出40岁的人剩余寿命变量的生存函数、死亡效力函数和密度函数形式。
解 由生命函数之间的关系,可以得出
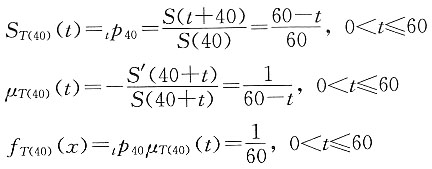
3. 已知
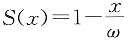
(0<x≤ω),且
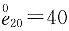
。计算Var[T(20)]。
解 由
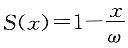
,可知X~U(0,ω),且有
T(20)~U(0,ω-20)
则

已知
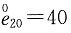
,即
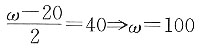
所以
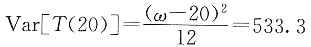
4. 已知
1|q
x+1=0.090,
2|q
x+1=0.170,q
x+3=0.250,计算q
x+1+q
x+2的值。
解 把q
x+3=0.250代入
2|q
x+1=0.170式中,得
2|q
x+1=p
x+1·p
x+2·q
x+3=0.170
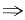
p
x+1p
x+2=0.680
上式与已知条件
1|q
x+1=p
x+1·q
x+2=0.090
联立求解,得
p
x+1=0.770,q
x+2=0.117
最后得
q
x+1+q
x+2=(1-p
x+1)+q
x+2=0.23+0.117=0.347
5. 设K是(97)的整数剩余寿命,试求Vat(K)。假设生命表如下:
x lx 97 150
98 100
99 40
100 0
解 方法一:
首先计算K的概率密度函数:
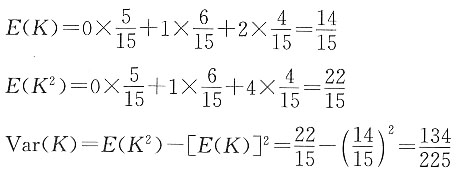
方法二:
首先计算K的生存函数:
则
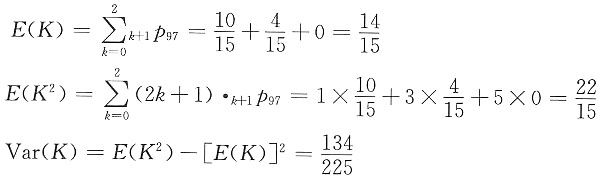
6. 已知
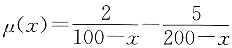
(40<x<100),试计算
30p
50。
解
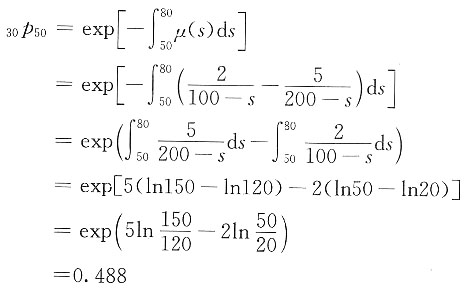
7. 某一人群,在出生时男女人数相等,且男性的死亡效力为μ
m(x)=0.09(x≥0),女性的死亡效力为μ
f(x)=0.07(x≥0)。求这个人群50岁的死亡概率q
50。
解 假设出生总人数是l
0,则男性能存活到50岁的人数为:
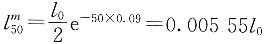
女性能存活到50岁的人数为:
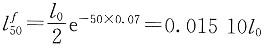
50岁时总存活人数为:
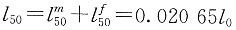
则50岁时男女人口结构比例分别为:
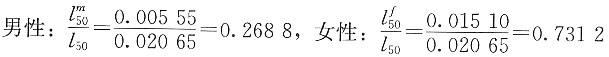
50岁时男女死亡概率分别为:
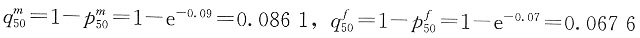
由全概率公式得这个人群50岁的死亡概率为:
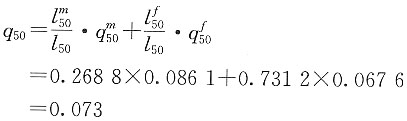
8. 证明下列不等式:
(1)

(2)
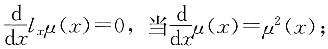
(3)
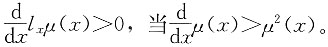
解
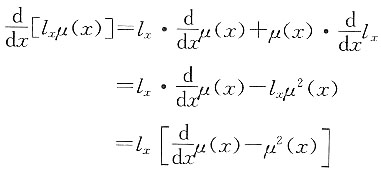
由此以上命题均成立。
9.

解

10.
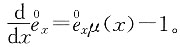
解
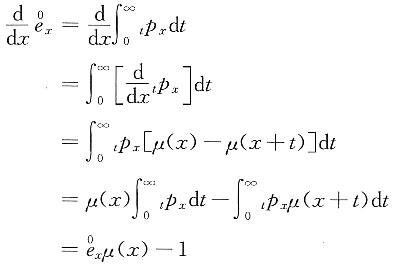
11. 已知
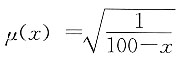
(0≤x<100),计算(40)剩余寿命的中位数。
解 令t
0.5代表剩余寿命的中位数,则
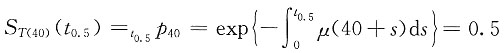
其中
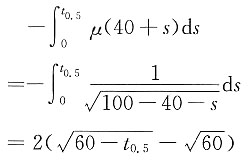
在
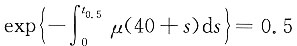
等式两边同时取对数,可得
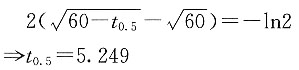
12. 已知T(x)是(x)剩余寿命随机变量,它的密度函数为f
T(t)=2e
-2t(t≥0)。计算:
(1)
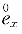
;
(2)Var[T(x)];
(3)剩余寿命的中位数。
解 根据剩余寿命T(x)的密度函数,可知T(x)服从λ=2的指数分布,因而
(1)

(2)
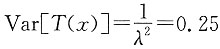
(3)
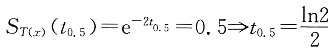
13. 已知
tp
x=(0.9)
t(t≥0),l
x+2=8.1,计算T
x+1。
解 由于
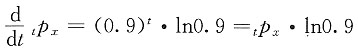
所以该剩余寿命服从常数死亡效力分布,μ=-ln0.9。
在常数死亡效力分布下,有

再根据
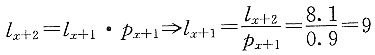
则有
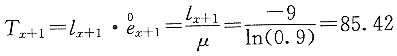
14. 相对于一个标准的生命表,另外一张生命表的死亡效力是它的2倍,即μ'(x)=2μ(x)。那么q'
x与2q
x具有怎样的大小关系?
解 因为
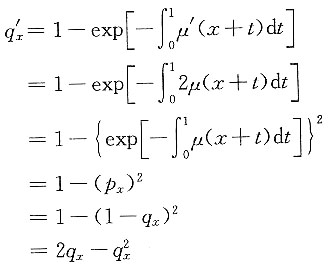
由此推出
q'
x<2q
x
15. 如下是一张选择期为2年的选择终极生命表:
[x] l
[x] l
x+2 x+2
82 … 6400 84
83 … 5080 85
84 … 3036 86
并且对于任意的x都有(1)3·q
[x]+1=4·q
[x+x];(2)4·q
x+2=5·q
[x+1]+1,计算l
[84]。
解
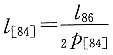
其中l
86已知,而
2p
[84]=p
[84]p
[84]+1=(1-q
[84])(1-q
[84]+1)
由已知条件推导出

则
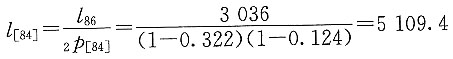
16. 在UDD假定下,用生命表函数表达
yq
x+t,假设0<t<1,0<y<1,且0<t+y<1。
解
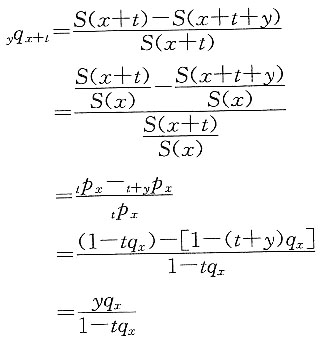
17. 已知q
70=0.40,q
71=0.50。f代表在死亡均匀分布假定下,(70)在70.5~71.5岁之间死亡的概率,g代表在CFM假定下,(70)在70.5~71.5岁之间死亡的概率,计算10000(g-f)。
解 (70)在70.5~71.5之间死亡的概率为:
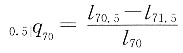
不妨假设l
70=100,则
l
71=l
70(1-q
70)=100×(1-0.4)=60
l
72=l
71(1-q
71)=60×(1-0.5)=30
在死亡均匀分布假定下,有

在CFM假定下,有
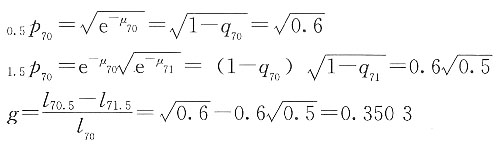
所以
10000(g-f)=3
18. 已知l
x=12,l
x+1=9。假设K为(x)在CFM假定下在前1/3年死亡的概率,L为(x)在死亡均匀分布假定下在后2/3年死亡的概率,试计算K+L的值。
解 在CFM假定下,有
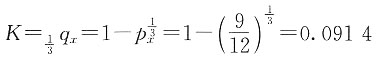
在死亡均匀分布假定下,有

则
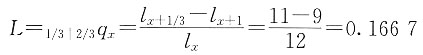
所以
K+L=0.0914+0.1667=0.2581
19. 已知
(1)μ(70.5)=0.01005;
(2)μ(71.5)=0.03046;
(3)μ(72.5)=0.05128。
假定死亡在分数时期服从均匀分布。计算一个70.5岁的人在2年内死亡的概率。
解 在均匀分布假定下,有
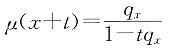
推导出
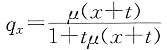
由题设条件可得
q
70=0.01,q
71=0.03,q
72=0.05
则
2q
70.5=1-
2p
70.5 =1-0.5p
70.5·p
71·
0.5p
72 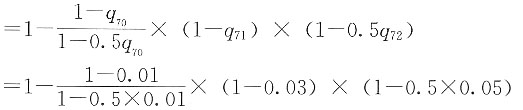
=0.059
20. 对于一个30岁的投保人,Z为终身寿险死亡即刻赔付1的现值变量。已知l
x=100-x(0≤x≤100),利息力恒定为0.05,计算f
Z(0.6)的值。
解 因为
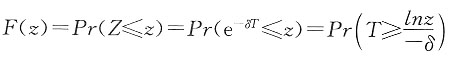
且由条件知剩余寿命服从de Moivre分布,即T~U(0,70),故
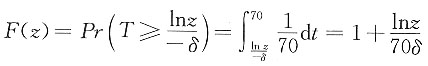
密度函数等于分布函数的导数
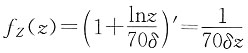
已知δ=0.05,z=0.6,代入上式得
f
Z(0.6)=0.48
21. 假设寿命X服从[0,110]上的均匀分布。对于一个40岁的投保人,Z为终身寿险死亡即刻赔付1的现值变量。已知年实质利率为2.5%,求Z的90%置信上限。
解 (40)的剩余寿命T服从均匀分布(0,70),其生存函数为:
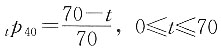
由题意,可得

Z的90%置信上限即为使F(z)=0.9的z值,即

解得
z=exp[(70-70×0.9)lnv]=0.84
22. 一个x岁的人投保死亡即刻赔付1的终身寿险,已知死亡力函数为常数μ,利息力恒定为0.05,趸缴净保费为0.6。保险公司经过对风险和利率的重新评估,决定将上述精算假设调整如下:
(1)μ
x(t)在原来的基础上增加0.02;
(2)利息力调整为0.04。
计算经过精算假设调整后的趸缴净保费。
解 在恒定死亡力和恒定利息力场合,容易验证趸缴净保费为:
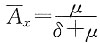
在调整以前有
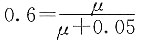
则求得
μ=0.075
调整以后
μ'=0.075+0.02=0.095,δ'=0.04
则调整后的趸缴净保费为:

23. z为(x)终身寿险死亡即刻赔付1的现值变量。已知剩余寿命T(x)的密度函数为
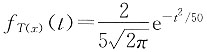
(t>0),利息力δ=0.05,求
和Var(z)的值。
解 (1)
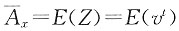
,则
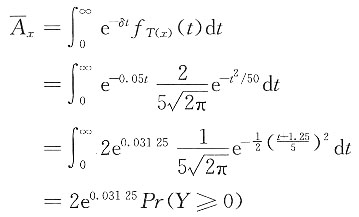
其中Y~N(-1.25,25),则
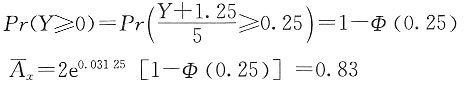
(2)因为
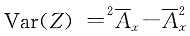
,其中

所以

24. (40)投保一终身寿险,Z为该终身寿险死亡即刻赔付的现值变量。已知
(1)给付金额b
t=1+0.2t;
(2)贴现v
t=(1+0.2t)
-2;
(3)
tp
40μ(40+t)=0.02(0≤t≤50)。
试计算Var(Z)。
解 给付函数和贴现函数都已知,容易得到现值函数为:
Z=b
tv
t=(1+0.2t)
-1 密度函数已知
f
T(t)=
tp
40μ(40+t)=0.02,0≤t≤50
则趸缴净保费为:
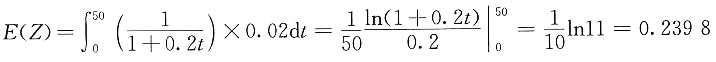
两倍利息力下,趸缴净保费为:
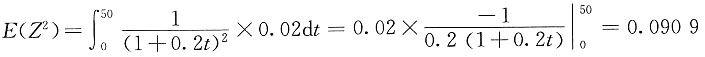
所以现值变量的方差为:
var(Z)=E(Z
2)-[E(Z)]
2=0.0909-0.2398
2=0.0334
25. 已知寿命服从ω=100的de Moivre分布,利息力恒定,且在该利息力下
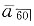
=40,终身寿险死亡即刻赔付1000元,求(40)的趸缴净保费。
解 一般情况下,如果剩余寿命T服从(0,ω-x)的均匀分布,即
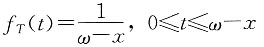
可以得到

本题中,T服从(0,60)的均匀分布,故所求的净保费为:
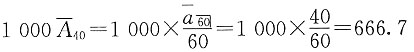
26. 一终身寿险的死亡即刻给付为1,并按δ=0.05的利息力返还趸缴净保费。若趸缴净保费是按恒定死亡力μ=0.06,恒定利息力2δ的净均衡原则计算,求趸缴净保费。
解 设死亡赔付现值变量为Z,趸缴净保费记作P。则根据题意,死亡即刻被保险人获得的受益金来自两个部分,一部分是死亡即刻给付的恒定受益金额1,另一部分是趸缴净保费P按照δ=0.05的利息力积累到死亡即刻的积累值Pe
δt,所以受益函数为:
b
t=1+Pe
δt,t≥0
贴现函数按照2δ利息力计量
v
t=v
t=e
-2δt,t≥0
死亡即刻赔付现值变量为:
Z=b
tv
t=(1+Pe
δt)e
-2δt=e
-2δt+Pe
-δt,t≥0
根据净均衡原则,有
P=E(Z)
又在死亡力恒定的条件下有
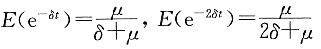
故
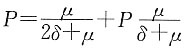
即
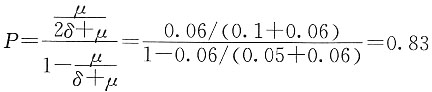
27. z
1是(x)投保死亡即刻赔付1的n年定期寿险的现值变量,z
2是(x)投保死亡即刻赔付1的n年定期两全险的现值变量。已知
(1)v
n=0.200;
(2)
np
x=0.450;
(3)E(z
2)=0.350;
(4)Var(z
2)=0.060。
试计算Var(z
1)。
解 令z
3为(x)投保期末赔付1的n年定期生存保险的现值变量,根据已知条件有
E(z
3)=v
n·
np
x=0.2×0.45=0.09
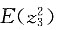
=v
2n·
np
x=0.04×0.45=0.018
根据定期两全险与定期寿险和定期生存险的关系,有
z
2=z
1+z
3 则
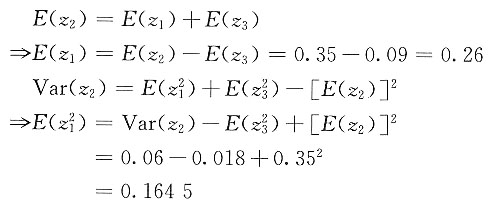
推导出
Var(z
1)=
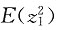
-[E(z
1)]
2=0.1645-0.26
2=0.0969
28. (40)投保死亡即刻赔付为1的20年延期终身寿险。已知l
x=100-x(0≤x≤100),利息力δ=0.05。设赔付现值变量为Z,求Z变量的重概率点和该点的概率值。
解 因为死亡服从de Moivre分布,故40岁的人剩余寿命的密度函数为:
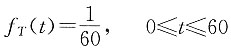
由于延期20年,所以赔付现值变量为:
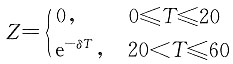
所以,z=0点为重概率点,该点概率值为:
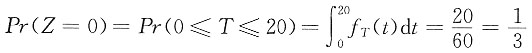

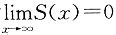 。
。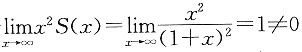 。该函数不可以作为生存函数。
。该函数不可以作为生存函数。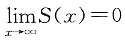 。该函数可以作为生存函数。
。该函数可以作为生存函数。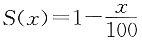 (0≤x≤100),请写出40岁的人剩余寿命变量的生存函数、死亡效力函数和密度函数形式。
(0≤x≤100),请写出40岁的人剩余寿命变量的生存函数、死亡效力函数和密度函数形式。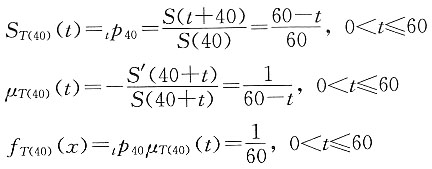
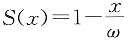 (0<x≤ω),且
(0<x≤ω),且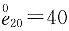 。计算Var[T(20)]。
。计算Var[T(20)]。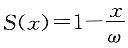 ,可知X~U(0,ω),且有
,可知X~U(0,ω),且有
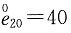 ,即
,即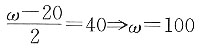
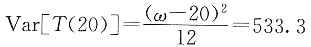
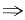 px+1px+2=0.680
px+1px+2=0.680
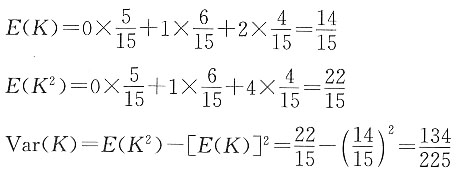

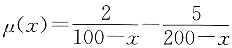 (40<x<100),试计算30p50。
(40<x<100),试计算30p50。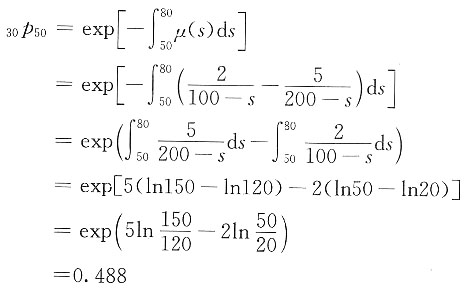
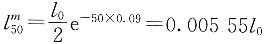
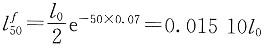
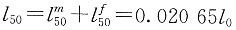
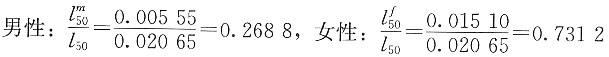
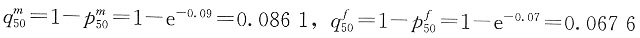
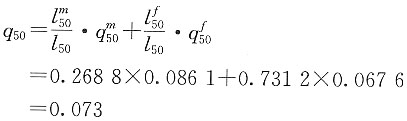

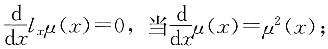
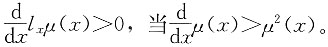
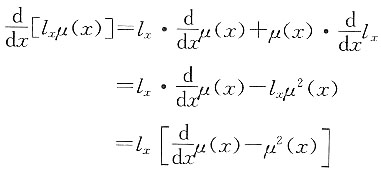


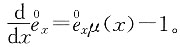
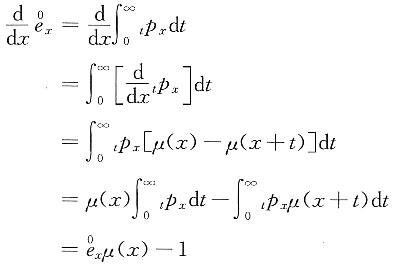
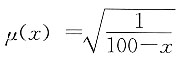 (0≤x<100),计算(40)剩余寿命的中位数。
(0≤x<100),计算(40)剩余寿命的中位数。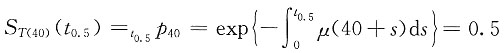
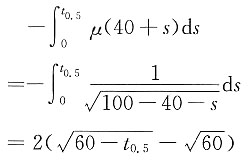
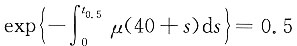 等式两边同时取对数,可得
等式两边同时取对数,可得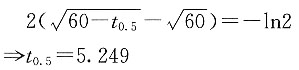
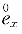 ;
;
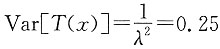
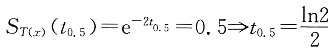
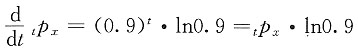

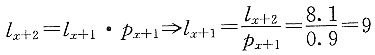
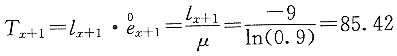
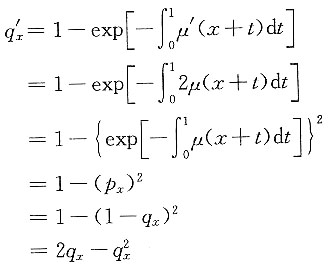
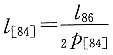

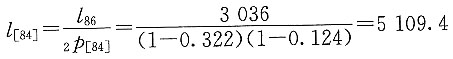
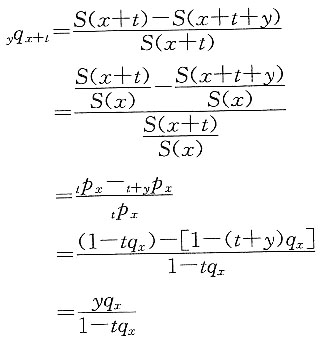
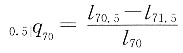

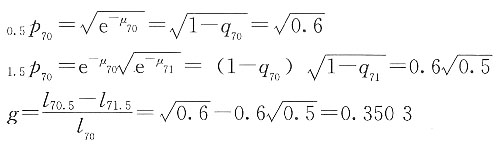
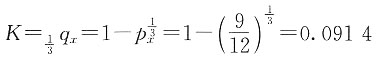

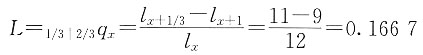
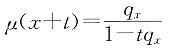
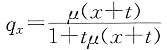
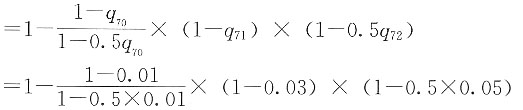
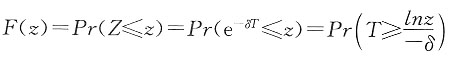
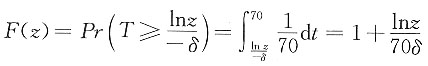
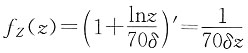
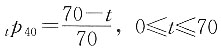


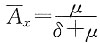
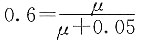

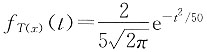 (t>0),利息力δ=0.05,求
(t>0),利息力δ=0.05,求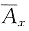 和Var(z)的值。
和Var(z)的值。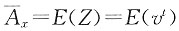 ,则
,则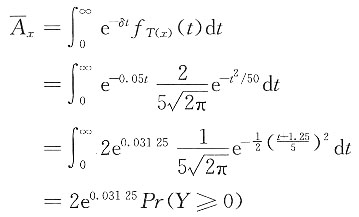
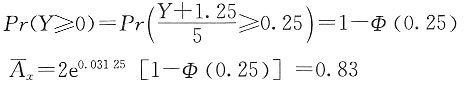
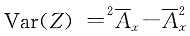 ,其中
,其中

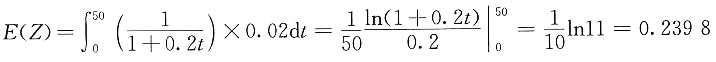
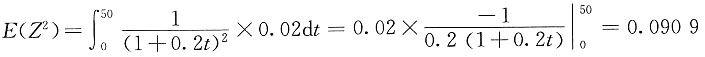
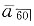 =40,终身寿险死亡即刻赔付1000元,求(40)的趸缴净保费。
=40,终身寿险死亡即刻赔付1000元,求(40)的趸缴净保费。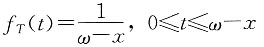

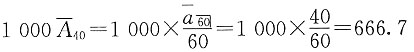
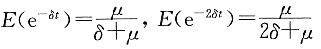
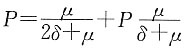
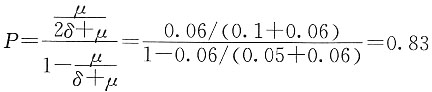
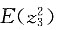 =v2n·npx=0.04×0.45=0.018
=v2n·npx=0.04×0.45=0.018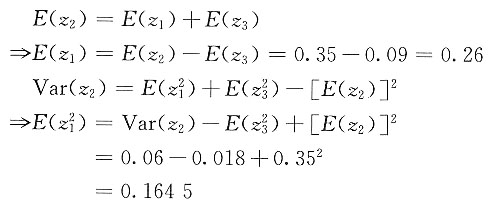
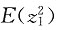 -[E(z1)]2=0.1645-0.262=0.0969
-[E(z1)]2=0.1645-0.262=0.0969