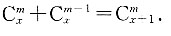一、选择题5. 已知函数f(x)=sin(2x+φ)，其中φ为实数，若
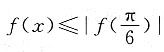
对x∈R恒成立，且
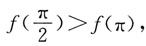
则f(x)的单调递增区间是______
A．
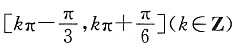
B．
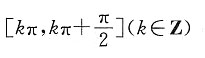
C．
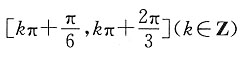
D．
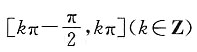
A B C D
C
[解析]
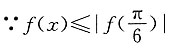
对x∈R恒成立，∴
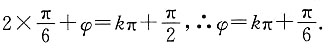
又
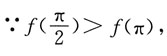
∴φ可取
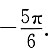
故
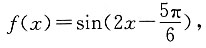
由
可得
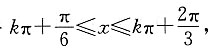
因此选C．
7. 已知|a+2b|+(c-a)
2=0，则代数式
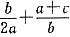
的值为_______．
A．
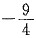
B．0
C．
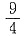
D．
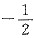
A B C D
A
[解析]本题主要考查代数式的运算．
由|a+2b|+(c-a)
2=0可知，a=-2b=c，则
．
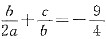
10. 复数
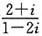
的共轭复数是______．
A．
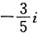
B．
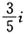
C．-i
D．i
A B C D
C
[解析]
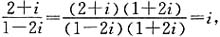
因此
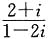
的共轭复数是-i．故选C．
二、填空题1.
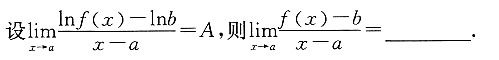
Ab
[解析] 由已知可补充定义f(a)=b，则有
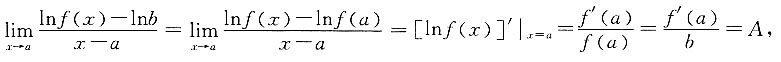
即f'(a)=Ab，于是
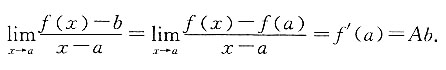
2. 已知
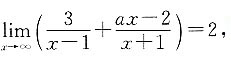
则a=______．
2
[解析]
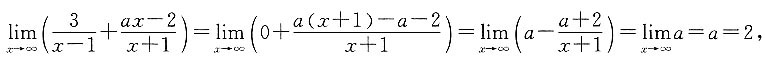
所以a=2．
3. 一物体(可视为质点)在力F=2i+3j-k的作用下由点A(-3，1，2)运动到点B(2，3，4)，则力做功为______焦耳．
14
[解析] 由题意可知位移
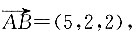
所以力做的功
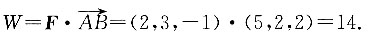
4. ______是依据数学教学目的和教学过程的客观规律而制定的指导数学教学工作的一般原理，它是数学教学经验的概括总结．
5. 在复平面内，O是坐标原点，
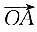
对应的复数为3-2i，将点A按向量a=1+i移动到点B，则移动后的向量
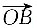
对应的复数为______．
4-i
[解析] (3-2i)+(1+i)=4-i，故平移后
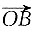
对应的复数为4-i．
三、解答题1. 小李在静止的河水中的游泳速度是2.5km/h，某河水流速度为2km/h．若该河宽400m，小李沿着河的正对岸游，想要正好游到河正对岸的便利店，问：小李能否到达目的地，若能则求出路程．若不能，小李到岸时距离目的地多远，给出能到达目的地的正确方案并求出路程．
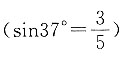
小李不能游到目的地，因为必须考虑水流的速度．
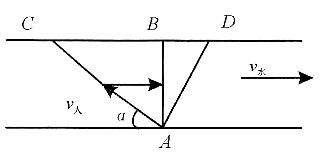
如图所示，设小李从A出发，B是便利店，因为水流的影响，小李实际到岸地点在便利店的下游D，则经过的路程为AD．
依题意知AB=400m，小李在河中游了
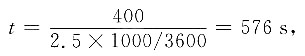
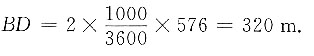
所以根据勾股定理可得
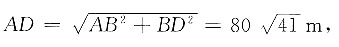
故小李实际经过的路程为
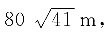
距离目的地320m；
要想到达便利店，小李应向上游方向游，如图所示，
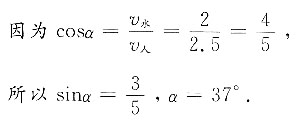
即应朝上游、与河岸成37°的方向游，才能正好到达便利店，此时经过的路程为400m．
2. 已知数列{a
n}为等比数列，数列{b
n}为等差数列，且满足
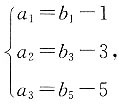
求等差数列{b
n}的公差d．
已知数列{b
n}为等差数列，设b
n=An+B．
数列{a
n}为等比数列，则
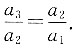
又因为
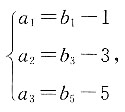
则
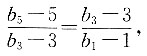
代入后可得
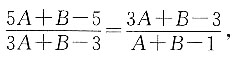
即(5A+B-5)(A+B-1)=(3A+B-3)
2，
化简可得A
2-2A+1=0，
解得A=1，
所以d=b
n-b
n-1=n+B-(n-1+B)=1，
即等差数列的公差d=1．
3. 求
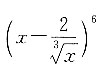
的展开式中有理项的系数和．
原式展开式的通项为
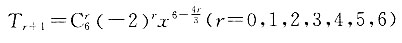
当r=0或3或6时，即第一项、第四项与第七项为有理项，
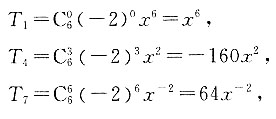
所以有理项的系数和为1-160+64=-95．
4. 此时汽车行驶了多长时间?
第一段路程，速度从0km/h到达80km/h所需要的时间为t
1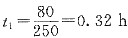 
；
第二段路程，汽车以80km/h匀速行驶0.5h，
t
2=0.5h；
第三段路程，汽车速度在12min内速度由80km/h均匀减为零，
则t
3=0.2h；
t
总=0.32+0.5+0.2=1.02h．
5. 此时汽车行驶的总路程是多少?
根据题干可画出速度关于时间的函数图象，则v和t的函数所围成的梯形的面积即为汽车行驶的总路程．
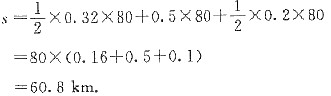
此时汽车行驶的总路程是60.8km．
6. 汽车修理好之后，若以38km/h的速度沿原路返回，则需要花多长时间?
，
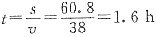
若以38km/h的速度沿路返回，则需1.6h．
7. 设
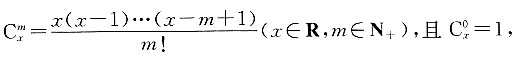
求证：
=______．
因为
所以
则B等于______
∴C=45°或C=135°，故B=105°或B=15°，故选D．
则
=______．
则|f(x)|在[-1，e]上最小值和最大值分别为______．
在[-1，1]上单调递减，在[1，e]上单调递增，所以最小值在x=1处取得，|f(1)|=0；|f(-1)|=4，|f(e)|=1，|f(-1)|＞|f(e)|，所以最大值为4，在x=-1处取得．
，可得
得证．
深色：已答题 浅色：未答题