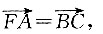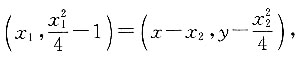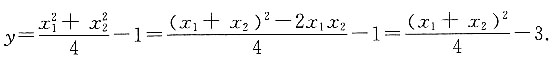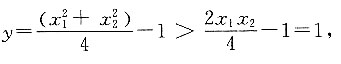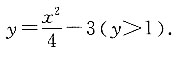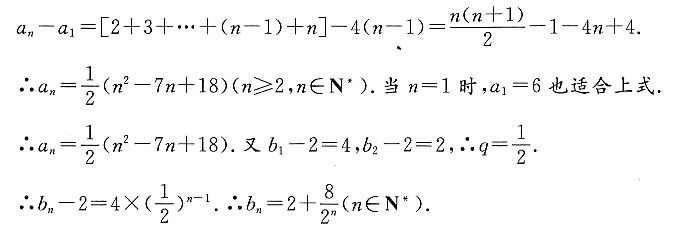一、选择题3. 现有练习本若干,分给甲、乙、丙、丁四个班,分法是:若分甲10本,则分乙8本;若分乙10本,则分丙8本;若分丙10本,则分丁8本.已知丁分得的练习本数比甲分得的练习本数的

少11本.由此可知,乙分得练习本______本.
A B C D
B
[解析] 各班分得的练习本数的比例关系如下:
甲:乙=5:4,乙:丙=5:4,丙:丁=5:4,所以,
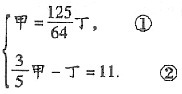
由①②得:丁=64,乙=
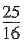
丁=
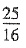
×64=100.
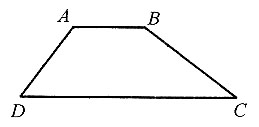
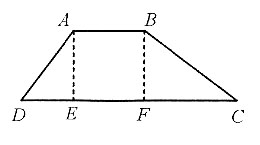
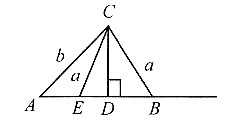
4. 如图,在梯形ABCD中,BC=6,CD=10,∠C=30°,∠D=45°,则AB=______.
A.
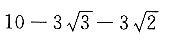
B.
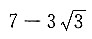
C.
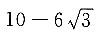
D.4
A B C D
B
[解析] 如图,作AE⊥DC交DC于E,BF⊥DC交DC于F,所以AE=BF=BC·sinC=3,
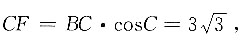
因为∠D=45°,所以DE=AE=3,则
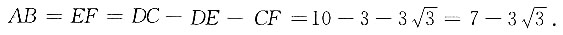
6. 一个球与它的外切圆柱、外切等边圆锥(圆锥的轴截面为正三角形)的体积之比______
- A.2:3:5
- B.2:3:4
- C.3:5:8
- D.4:6:9
A B C D
D
[解析] 作出轴截面,圆内切于一个正方形和一个等边三角形,易知正方形的边长等于圆的直径,圆心是等边三角形的中心,设球的半径为r,则外切圆柱的底面圆的半径为r,高为2r,外切圆锥的底面圆的半径为

高为3r,所以球的体积
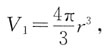
外切圆柱的体积V
2=πr
2×2r=2πr
3,外切等边圆锥的体积
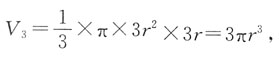
所以

所以选D.
二、填空题1. 若向量e
1,e
2不共线,且向量a=2e
1-2e
2,b=4e
1+2e
2,c=-3e
1-2e
2,则a可用b,c表示为a=______.
5b+6c
[解析] 设a=xb+yc,即2e
1-2e
2=x(4e
1+2e
2)+y(-3e
1-2e
2),
∴2e
1-2e
2=(4x-3y)e
1+(2x-2y)e
2,∵e
1,e
2不共线,
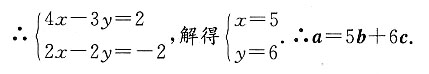
2. 二次函数y=ax
2+bx+c(x∈R)的部分对应值如下表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
则不等式ax
2+bx+c<0的解集是______.
{x|-2<x<3}
[解析] 由表可得方程ax2+bx+c=0的两根为-2,3,
∴y=ax2+6x+c=a(x+2)(x-3).将(-3,6)代入二次函数得a=1>0,
∴不等式ax2+bx+c<0的解集为{x|-2<x<3}.
3. 已知一圆心角为150°的扇形的周长为27,则该圆的半径为______.(圆周率取3)
6
[解析] 依题意知,扇形的周长
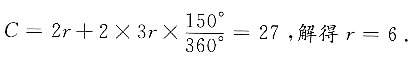
4. 现在需要制作一批道路交通标志牌,若甲单独完成,则3天可制作a个;若甲、乙共同完成,则5天可制作b个;若乙单独完成,完成(a+b)个需要______天.
[解析]本题主要考查代数式的实际应用.
依题意可知,甲的效率为
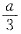
个/天;甲、乙共同的效率为
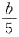
个/天,则乙的效率为
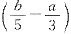
个/天.所以乙单独完成(a+b)个所需的时间为
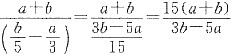
天.
5. 已知对数函数f(x)=lg(x
2+1)-1,则f[f(0)]=______.
-lg5
[解析] f(0)=lg1-1=-1,则f[f(0)]=f(-1)=lg2-1=-lg5.
三、解答题已知f(x)=x㏑x-ax,g(x)=-x2-2.1. 对一切x∈(0,+∞),f(x)≥g(x)恒成立,求实数a的取值范围;
对于一切x∈(0,+∞),f(x)≥g(x)恒成立.
即证
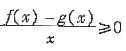
恒成立.即㏑x-a+x+
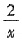
≥0恒成立.
令h(x)=㏑x-n+x+

,则
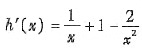
,令h′(x)=0,则h(x)的极小值点为x=1.
代入h(x),则㏑l-a+1+2≥0,即当a≤3时,对于一切x∈(0,+∞),f(x)-g(x)≥0恒成立.
2. 当a=-1时.求函数f(x)在[m,m+3](m>0)上的最小值.
当a=-1时,f(x)=x㏑x+x,f'(x)=㏑x+2,
令f'(x)=㏑x+2=0,则x=e-2.当x∈[e-2,+∞)时,f(x)为增函数,当x∈(0,e-2)时,f(x)为减函数.
若e-2∈[m,m+3],则f(x)最小值为f(e-2)=-e-2;
若e-2<m,则f(x)最小值为f(m)=m(㏑m+1);
若e-2>m+3,则f(x)最小值为f(m+3)=(m+3)[㏑(m+3)+1].
3. 若α=2β=60°,问该船有无触礁危险?如果没有,请说明理由:如果有,那么该船自B处向东航行多少距离有触礁危险?
解:作MC⊥AB,垂足为C,由已知α=60°,β=30°,所以∠ABM=120°.∠AMB=30°.
所以BM=AB=4,∠MBC=60°,所以MC=BM·sin60°=
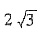
<3.5,所以该船有触礁的危险.设该船自B向东航行至点D有触礁危险,则MD=3.5,在△MBC中,BM=4,BC=2
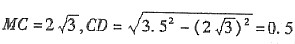
,所以,BD=1.5(km).
所以,该船自西向东航行1.5km会有触礁危险.
4. 当α与β满足什么条件时,该船没有触礁危险?
设CM=x,在△MAB中,由正弦定理得,
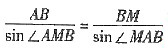
,
即
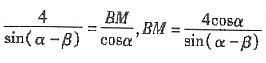
,
而
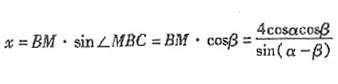
,
所以,当x>3.5,即
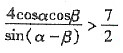
,
即
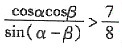
时,该船没有触礁危险.
5. 求证:
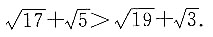
要证明
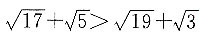
成立,只需证明
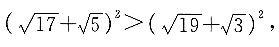
即证明

只需证明
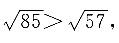
即证明85>57,这显然成立,
所以
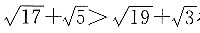
得证.
6. 已知函数
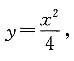
如图过点M(0,-1)作斜率为k的直线l交该函数图象于A,B两点.若该函数曲线的焦点F与A,B,C三点按图中顺序连接成平行四边形,求点C的轨迹方程.
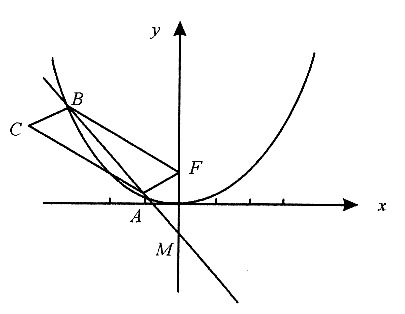
由题干可知,抛物线焦点坐标为F(0,1),
设A,B,C三点坐标分别为
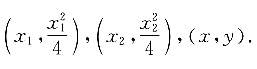
因为F(0,1),M(0,-1),
所以
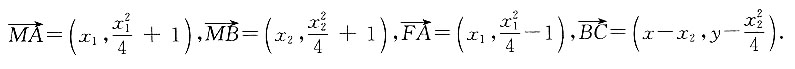
又因为M、A、B三点共线,
所以
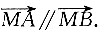
所以
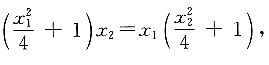
即x
1x
2(x
1-x
2)=4(x
1-x
2).
因为x
1≠x
2,
所以x
1x
2=4.
又因为四边形ACBF为平行四边形,
所以
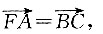
所以
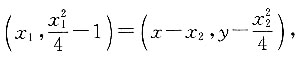
所以
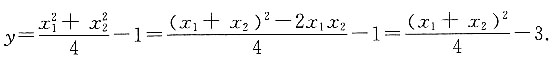
又因为x
1=x-x
2,即x=x
1+x
2,
所以x
2=4y+12.
又因为
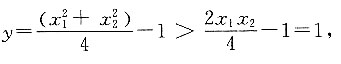
所以点C的轨迹方程是
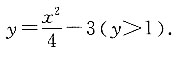
7. 设数列{a
n},{b
n}满足a
1=b
1=6,a
2=b
2=4,a
3=b
3=3,且数列{a
n+1-a
n}{n∈N
*)是等差数列,{b
n-2}是等比数列,求{a
n}和{b
n}的通项公式.
由已知a
2-a
1=-2,a
3-a
2=-1,d=-1-(-2)=1,
∴a
n+1-a
n=(a
2-a
1)+(n-1)d=-2+(n-1)×1=n-3,
即a
n-a
n-1=n-4(n≥2).
故a
n-a
n-1=n-4,
a
n-1-a
n-2=(n-1)-4,
…
a
3-a
2=3-4,
a
2-a
1=2-4.
以上各式左右分别相加得
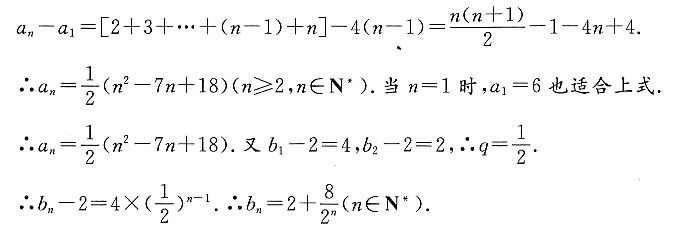
 少11本.由此可知,乙分得练习本______本.
少11本.由此可知,乙分得练习本______本.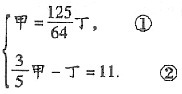
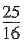 丁=
丁=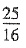 ×64=100.
×64=100.
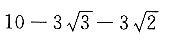
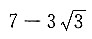
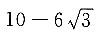
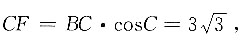 因为∠D=45°,所以DE=AE=3,则
因为∠D=45°,所以DE=AE=3,则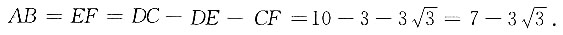

 高为3r,所以球的体积
高为3r,所以球的体积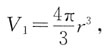 外切圆柱的体积V2=πr2×2r=2πr3,外切等边圆锥的体积
外切圆柱的体积V2=πr2×2r=2πr3,外切等边圆锥的体积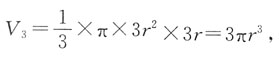 所以
所以 所以选D.
所以选D.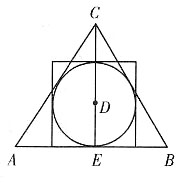
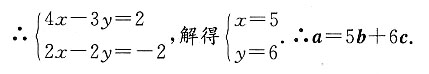
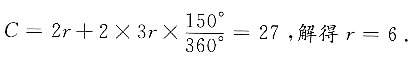
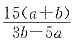
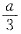 个/天;甲、乙共同的效率为
个/天;甲、乙共同的效率为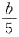 个/天,则乙的效率为
个/天,则乙的效率为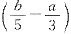 个/天.所以乙单独完成(a+b)个所需的时间为
个/天.所以乙单独完成(a+b)个所需的时间为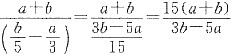 天.
天.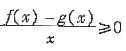 恒成立.即㏑x-a+x+
恒成立.即㏑x-a+x+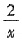 ≥0恒成立.
≥0恒成立. ,则
,则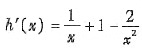 ,令h′(x)=0,则h(x)的极小值点为x=1.
,令h′(x)=0,则h(x)的极小值点为x=1.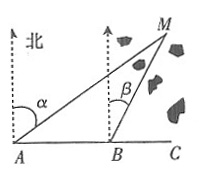
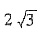 <3.5,所以该船有触礁的危险.设该船自B向东航行至点D有触礁危险,则MD=3.5,在△MBC中,BM=4,BC=2
<3.5,所以该船有触礁的危险.设该船自B向东航行至点D有触礁危险,则MD=3.5,在△MBC中,BM=4,BC=2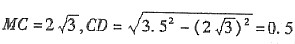 ,所以,BD=1.5(km).
,所以,BD=1.5(km).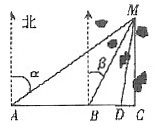
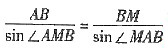 ,
,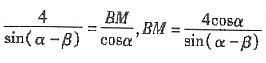 ,
,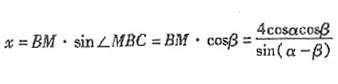 ,
,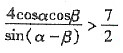 ,
,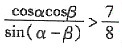 时,该船没有触礁危险.
时,该船没有触礁危险.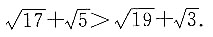
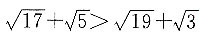 成立,只需证明
成立,只需证明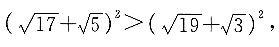 即证明
即证明
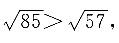 即证明85>57,这显然成立,
即证明85>57,这显然成立,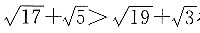 得证.
得证.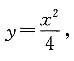 如图过点M(0,-1)作斜率为k的直线l交该函数图象于A,B两点.若该函数曲线的焦点F与A,B,C三点按图中顺序连接成平行四边形,求点C的轨迹方程.
如图过点M(0,-1)作斜率为k的直线l交该函数图象于A,B两点.若该函数曲线的焦点F与A,B,C三点按图中顺序连接成平行四边形,求点C的轨迹方程.
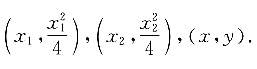
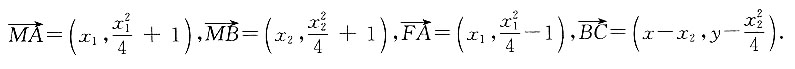
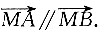
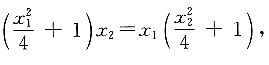 即x1x2(x1-x2)=4(x1-x2).
即x1x2(x1-x2)=4(x1-x2).