一、选择题3. 函数
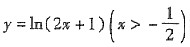
的反函数是______.
A.
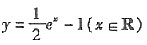
B.
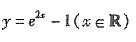
C.
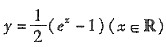
D.
A B C D
C
[解析] 由y=㏑(2x+1)反解得
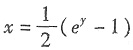
,所以
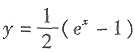
,又因为原函数定义域为
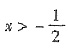
,y∈R,所以反函数定义域为x∈R,故选C.
4. 已知平面直角坐标系内有一个圆,其方程为
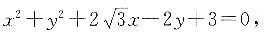
若直线
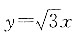
沿x轴平移后与圆相切,则移动后的直线在y轴上最小的截距为______.
A B C D
C
[解析] 圆的方程可以化简为
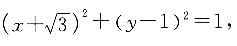
圆心为
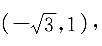
半径为1.设平移后的直线方程为
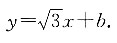
直线与圆相切,即与圆心的距离为半径,利用点到直线的距离公式可得,
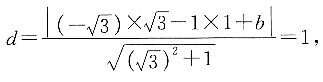
化简可得,|b-4|=2,解得b=2或b=6,要使截距最小,则取b=2.
5. 平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|=______.
A.
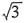
B.
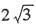
C.4
D.12
A B C D
B
[解析] a=(2,0),|a|=2,|b|=1,<a,b>=60°,
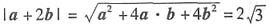
,故选B.
10. 定义在R上的任意函数f(x),都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,如果f(x)=lg(10
x+1),那么______.
A.g(x)=x,h(x)=lg(10
x+10
-x+2)
B.
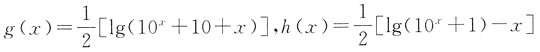
C.
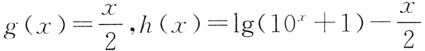
D.
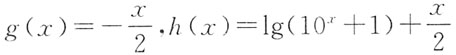
A B C D
C
[解析] f(-x)=lg(10
-x+1)=
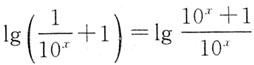
=lg(10
x+1)-lg10
x=lg(10
x+1)-x,A、B、D经过验证都不正确.对于选项C,g(x)+h(x)=lg(10
x+1)=f(x),g(x)显然为奇函数,
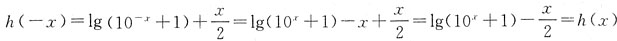
,即h(x)为偶函数,故选C.
二、填空题1. 用反证法证明命题“a,b∈N,ab可以被5整除,那么a,b中至少有一个能被5整除.”那么假设的内容是______.
a,b中没有一个能被5整除
[解析] “至少有n个”的否定是“最多有n-1个”.
2. 某次考试及格与不及格人数比为11:7,把及格与不及格人数分布情况制成扇形统计图,则表示及格人数的扇形圆心角的度数是______.
220°
[解析] 根据样本比例制作扇形统计图,则

所以表示及格人数的扇形圆心角的度数
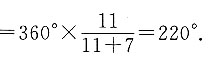
3. 已知奇函数y=f(x)的图象关于
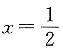
对称且周期为2,则f(1)+f(2)+…+f(9)+f(10)=______.
0
[解析] 因为y=f(x)为奇函数,则f(1)=-f(-1),f(x)是周期为2的周期函数,则f(x)=f(x+2),当x=-1时,f(-1)=f(1),所以f(-1)=-f(-1),即f(1)=f(-1)=0.已知函数关于
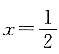
对称,则f(0)=f(1)=0,f(0)=f(2)=f(4)=f(6)=f(8)=f(10)=0,f(1)=f(3)=f(5)=f(7)=f(9)=0.所以原式=0.
4. 红、黄两个箱子内分别放有标有数字1,2,3的大小相同的球,现从两个箱子中各摸出一个球,则两球之和为偶数的概率为______.
[解析] 依题意,在两个箱子中各摸出一个球共有9种情况,两球之和为偶数的有5种情况,所以两球之和为偶数的概率为
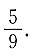
5. 若x
1,x
2,x
3的方差为2,则3x
1+5,3x
2+5,3x
3+5的方差为______.
18
[解析] x1,x2,x3的方差D(X)=2,则3x1+5,3x2+5,3x3+5的方差D(3X+5)=32D(X)=18.
三、解答题设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.1. 若∠BFD=90°,△ABD的面积为
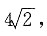
求p的值及圆F的方程;
由已知可得△BFD为等腰直角三角形,|BD|=2p,圆F的半径
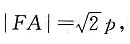
由抛物线定义可知A到l的距离
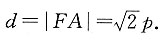
因为△ABD的面积为
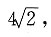
所以
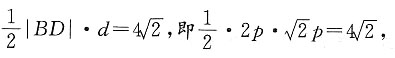
解得p=-2(舍去),或p=2.所以F(0,1),圆F的方程为x
2+(y-1)
2=8.
2. 若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
因为A,B,F三点在同一直线m上,所以AB为圆F的直径,∠ADB=90°.
由抛物线定义知

所以∠ABD=30°,m的斜率为

当m的斜率为
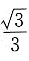
时,由已知可设
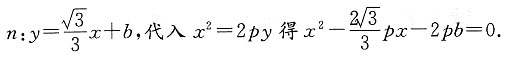
由于n与C只有一个公共点,故
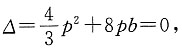
解得
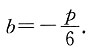
因为m的截距
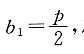
所以
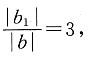
所以坐标原点到m,n距离的比值为3.
当m的斜率为
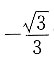
时,由图形的对称性可知,坐标原点到m,n距离的比值也为3.
3. 求抛物线的方程及焦点坐标;
已知点A(2,2)在抛物线上,
代入抛物线有2
2=2p×2=4p,故p=1,抛物线方程为y
2=2x.
焦点坐标为
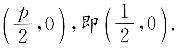
4. O为直角坐标系的原点,求线段OA的垂直平分线与抛物线的交点.
已知点A(2,2),O为坐标原点,
则线段OA的斜率为
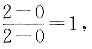
所以其垂直平分线的斜率为-1.
线段OA的中点坐标为(1,1),
故线段OA的垂直平分线的方程为y=-x+2.
要求线段OA的垂直平分线与抛物线的交点,则联立两方程得
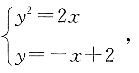
解得
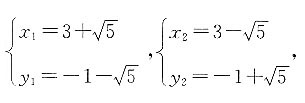
故交点分别为
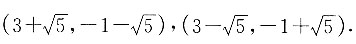

5. 求a
2,a
3;
因为
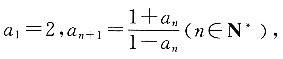
所以
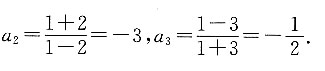
6. 求a
1·a
2·a
3…·a
1602.
由题意可知,
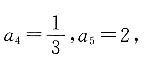
以此类推,可以发现数列{a
n}的周期为4,
且a
1=a
5,a
1·a
2·a
3·a
4=1,
所以a
1·a
2·a
3…a
1602=a
1601·a
1602=a
1·a
2=-6.
7. 已知方程x
2-ax+1=0至少有一个实根,求实数a的取值范围.
假设方程没有实数根,则需满足a2-4<0,即-2<a<2.所以方程至少有一个实根时,a的取值范围为(-∞,-2]∪[2,+∞).
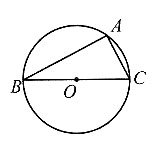
8. 直径所对应的圆周角是直角;
如图所示,BC为⊙O的直径,A为圆上不同于B、C的一点.
如图可知,
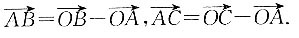
因为
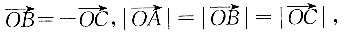
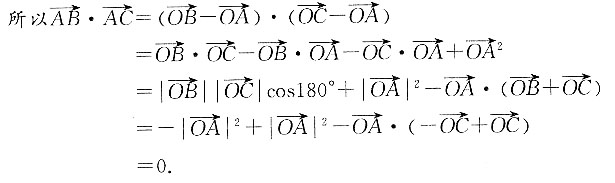
所以

即∠BAC=90°.
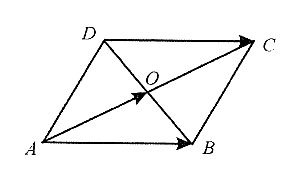
9. 平面上对角线互相平分的四边形是平行四边形.
如图所示,ABCD为四边形,O分别为AC、BD的中点.
由图可知,
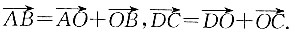
因为对角线相互平分,
所以
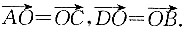
所以
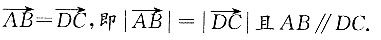
所以该四边形是平行四边形.