银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
教师公开招聘考试中学数学分类模拟题96
一、选择题
1. 我国最常用的教学组织形式是______．
A.班级教学
B.小组教学
C.个别教学
D.道尔顿制教学
A
B
C
D
A
[解析] 班级教学是指把学生按照年龄与知识程度编成固定的班级，教师按照固定的课程表和统一的进度，并主要以课堂讲授的方式分科对整个班级学生进行同样内容的教学，是我国最常用的教学组织形式．
2. 在
的展开式中的常数项是______．
A.-448
B.-1120
C.448
D.1120
A
B
C
D
D
[解析] 根据通项公式可得，
因为求常数项，故令8-2r=0，即r=4，所以
3. 已知函数f(x)=2x-5，h(x)=f
2
(x)-20，则h(x)=f(x)的解的个数为______．
A.0
B.1
C.2
D.3
A
B
C
D
C
[解析] h(x)=(2x-5)
2
-20=4x
2
-20x+5，h(x)=f(x)
4x
2
-20x+5=2x-5，解方程得
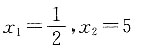
，所以解的个数为2，答案选C．
4. 当n→∞时，
为等价无穷小，则k=______．
A．
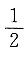
B．2
C．1
D．-2
A
B
C
D
B
[解析] 当n→∞时，
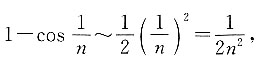
又因为当n→∞时，
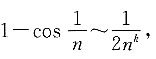
即当n→∞时，
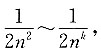
所以k=2．
5. 复数
表示的复平面内的点位于______
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
B
C
D
D
[解析]
它所表示的复平面内的点是
位于第四象限．
6. 设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于A，B两点，|AB|为C的实轴长的2倍，则C的离心率为______．
A．
B．
C．2
D．3
A
B
C
D
B
[解析] 由题意知
则
由离心率公式的
所以
故选B．
7. 己知
且
时
则y=______．
A．tan2x
B．
C．
D．
A
B
C
D
D
[解析]
又因为当
时，
即
解得
所以
8. 下列关于初中数学教学建议说法错误的是______．
A.数学教学活动要注重课程目标的整体实现
B.重视学生在学习活动中的主导地位
C.注重学生对基础知识、基本技能的理解和掌握
D.感悟数学思想，积累数学活动经验
A
B
C
D
B
[解析] 《义务教育数学课程标准》指出，数学教学活动要注重课程目标的整体实现；重视学生在学习活动中的主体地位；注重学生对基础知识、基本技能的理解和掌握；感悟数学思想，积累数学活动经验；关注学生情感态度的发展；合理把握“综合与实践”的实施等．因此本题选B．
9. 新课程的核心理念是______．
A.联系生活学数学
B.培养学生的学习兴趣
C.掌握知识培养能力
D.为了每一位学生的发展
A
B
C
D
D
[解析] 新课程的核心理念是以学生发展为本，让学生参与是新课程实施的核心．故选D．
10. “已知函数满足f(x-1)=f(x+1)，f(0)=1，求f(6)的值．求解过程为：因为当x=1时，f(0)=f(2)，当x=3时，f(2)=f(4)，当x=5时，f(4)=f(6)，故可得到：f(6)=f(4)=f(2)=f(0)=1．”上述问题的解答，利用的是函数的______．
A.定义域与值域
B.单调性
C.奇偶性
D.周期性
A
B
C
D
D
[解析] 根据题干可知，求值过程利用了函数的周期性，将f(6)与f(0)建立联系，进而求出f(6)的值．
二、填空题
1. 设等比数列的首项为a
1
，公比为q(q≠0)。要使此数列中奇偶项异号，则q______0(填“＞”“＜”或“=”)．
＜
[解析] 要使此数列中奇偶项异号，则只有公比为负的情况，即q＜0．
2. 若函数
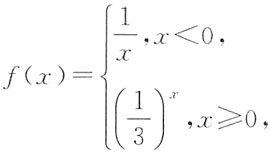
则不等式
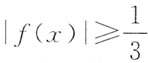
的解集为______．
[-3，1]
[解析] 依题可得
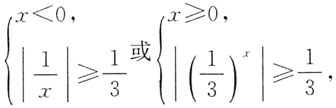
解之得-3≤x＜0或0≤x≤1，所以不等式
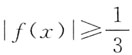
的解集为[-3，1]．
3. 一个底面边长为
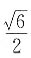
，侧棱长为
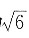
的正六棱柱的所有顶点都在一个球面上，则此球的体积为______．
[解析] 球的直径等于正六棱柱的体对角线长，设球的半径为R，由已知可得
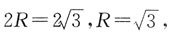
所以球的体积为
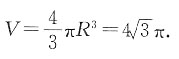
4. 设
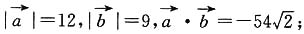
则
的夹角θ为______．
135°
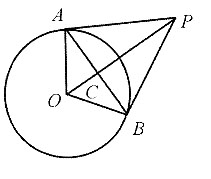
5. 圆外一点P与圆心O的距离是
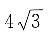
，过点P作圆的切线交圆于A、B两点，已知AB=6，则圆的半径r=______．
[解析] 如图所示，连接OP交AB于C，易知OP⊥AB，
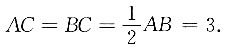
又因为PA、PB是圆的切线，所以∠PAO=∠PBO=90°，因此△AOP∽△COA，
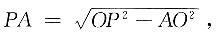
所以
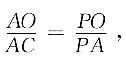
即
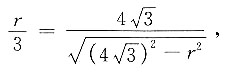
解得
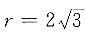
或r=6(r＞0)．因为圆外一点P与圆心O的距离是
故r=6不符合要求，所以
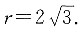
三、解答题
1. 如图所示，已知α∥β，γ∩α=n，γ∩β=b．证明：a∥b．
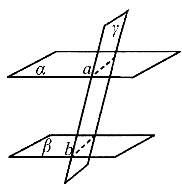
又因为
解方程组：
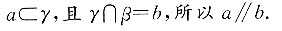
2.
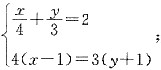
原方程组可化为
，
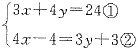
②-①可得x=7y-17③，
将③代入①中，可解得
．
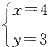
3.
原方程组可化为
，
整理可得
，
①-②，可解得
．
[解析]本题主要考查方程组的计算．
已知半径为R的圆球，放在一直径为
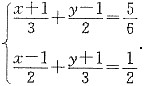
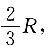高为R的空心无盖圆柱形容器上．(容器的厚度忽略不计)．
求：
4. 球的顶端到容器底面的距离L；
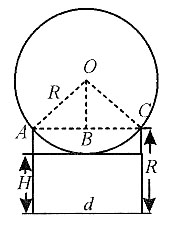
如图所示，沿圆柱的轴作切面，
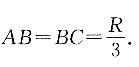
则在Rt△OBA中，
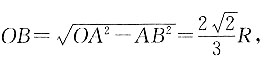
所以球的顶端到容器底面的距离
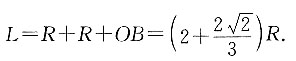
5. 向容器内注水，当水面刚好与球面相切时，水的体积．
由图可知，水面与球面相切时的高度为H，则
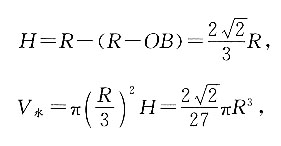
因此水面刚好与球面相切时，水的体积为
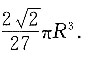
6. 计算积分
已知函数
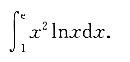
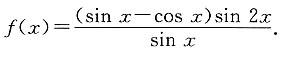
7. 求f(x)的定义域及最小正周期；
由sin x≠0得x≠kπ(k∈Z)，故f(x)的定义域为{x∈R|x≠kπ，k∈Z}．
因为
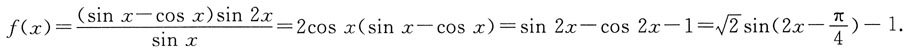
所以f(x)的最小正周期
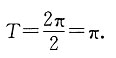
8. 求f(x)的单调递增区间．
函数y=sin x的单调递增区间为
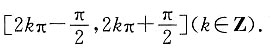
由
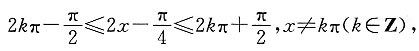
得
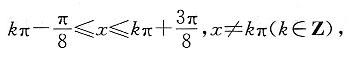
所以f(x)的单调递增区间为
一、选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
三、解答题
1
2
3
4
5
6
7
8
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
的展开式中的常数项是______．
因为求常数项，故令8-2r=0，即r=4，所以
4x2-20x+5=2x-5，解方程得
，所以解的个数为2，答案选C．
为等价无穷小，则k=______．
又因为当n→∞时，
即当n→∞时，
所以k=2．
表示的复平面内的点位于______
它所表示的复平面内的点是
位于第四象限．
则
由离心率公式的
所以
故选B．
且
时
则y=______．
又因为当
时，
即
解得
所以
则不等式
的解集为______．
的解集为[-3，1]．
，侧棱长为
的正六棱柱的所有顶点都在一个球面上，则此球的体积为______．
所以球的体积为
则
的夹角θ为______．
，过点P作圆的切线交圆于A、B两点，已知AB=6，则圆的半径r=______．
又因为PA、PB是圆的切线，所以∠PAO=∠PBO=90°，因此△AOP∽△COA，
所以
即
解得
或r=6(r＞0)．因为圆外一点P与圆心O的距离是
故r=6不符合要求，所以
，
．
，
，
．
高为R的空心无盖圆柱形容器上．(容器的厚度忽略不计)．
所以f(x)的最小正周期
得
深色：已答题 浅色：未答题