一、单项选择题2. 有一笔国债,5年期,溢价20%发行,票面利率10%,单利计息(复利折现),到期一次还本付息,其到期收益率是______。
- A.4.23%
- B.5.23%
- C.4.57%
- D.4.69%
A B C D
C
[解析] 本题的主要考核点是债券到期收益率的计算。债券的到期收益率是指债券的本金和利息流入的现值等于其购买价格时的折现率。由于在本题中属于溢价购买,所以,购买价格等于其面值×(1+20%)。计算到期收益率是求解含有折现率的方程,即:现金流出的现值=现金流入的现值。
假设面值为M,到期收益率为i,则有:M×(1+20%)=M×(1+5×10%)×(P/F,i,5)
(P/F,i,5)=1.2/(1+5×10%)=0.8
查表得i=4%,(P/F,4%,5)=0.8219
i=5%,(P/F,5%,5)=0.7835
则:
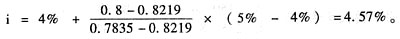
三、计算分析题A公司2017年3月4日发行公司债券,每张面值1000元,票面利率10%,5年期。A公司适用的所得税税率为25%。
要求通过计算回答下列互不相关的几个问题:1. 假定每年3月3日付息一次,到期按面值偿还。发行价格为1060元/张,发行费用为6元/张,计算该债券的税后资本成本。
假设债券的税前资本成本为r,则有:NPV=1000×10%×(P/A,r,5)+1000×(P/F,r,5)-(1060-6)
当r=8%,NPV=1000×10%×(P/A,8%,5)+1000×(P/F,8%,5)-1054=100×3.9927+1000×0.6806-1054=25.87(元)
当r=10%,NPV=1000×10%×(P/A,10%,5)+1000×(P/F,10%,5)-1054=100×3.7908+1000×0.6209-1054=-54.02(元)

债券的税后资本成本=8.65%×(1-25%)=6.49%
2. 假定每年3月3日付息一次,到期按面值偿还。发行价格为1000元/张,假设不考虑发行费用,计算该债券的税后资本成本。
由于平价发行,同时又不考虑发行费用,所以直接用简化公式即可计算。债券的税后资本成本=10%×(1-25%)=7.5%
3. 假定每年3月3日付息一次,到期按面值偿还。B公司2020年3月4日按每张1120元的价格购入该债券并持有到期,计算该债券的到期收益率。
NPV=1000×10%×(P/A,r,2)+1000×(P/F,r,2)-1120
当r=3%,NPV=1000×10%×(P/A,3%,2)+1000×(P/F,3%,2)-1120=100×1.9135+1000×0.9426-1120=13.95(元)
当r=5%,NPV=1000×10%×(P/A,5%,2)+1000×(P/F,5%,2)-1120=100×1.8594+1000×0.907-1120=-27.06(元)

4. 假定每年付息两次,每间隔6个月付息一次,到期按面值偿还。B公司2020年3月4日按每张1020元的价格购入该债券并持有到期,计算该债券的报价年到期收益率和有效年到期收益率。
NPV=1000×5%×(P/A,r,4)+1000×(P/F,r,4)-1020
当r=4%,NPV=1000×5%×(P/A,4%,4)+1000×(P/F,4%,4)-1020=50×3.6299+1000×0.8548-1020=16.30(元)
当r=5%,NPV=1000×5%×(P/A,5%,4)+1000×(P/F,5%,4)-1020=50×3.5460+1000×0.8227-1020=-20(元)
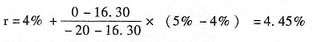
债券的报价年到期收益率=4.45%×2=8.9%
债券的有效年到期收益率=(1+4.45%)
2-1=9.1%
5. 假定每年3月3日付息一次,到期按面值偿还,报价折现率为12%。B公司2019年3月4日购入该债券并持有到期,计算确定当债券价格低于什么水平时,B公司才可以考虑购买。
债券价值=1000×10%×(P/A,12%,3)+1000×(P/F,12%,3)=100×2.4018+1000×0.7118=951.98(元)
所以,当债券价格低于951.98元时,B公司才可以考虑购买。
6. 假定每年付息两次,每间隔6个月付息一次,到期按面值偿还。年折现率为12%,B公司2019年3月4日购入该债券并持有到期,计算确定当债券价格低于什么水平时,B公司才可以考虑购买。
债券价值=1000×5%×(P/A,6%,6)+1000×(P/F,6%,6)=50×4.9173+1000×0.7050=950.87(元)
所以,当债券价格低于950.87元时,B公司才可以考虑购买。
7. 假定到期一次还本付息,单利计息,复利折现,折现率为12%。B公司2019年3月4日购入该债券并持有到期,计算确定当债券价格低于什么水平时,B公司才可以考虑购买。
债券价值=1000×(1+5×10%)/(1+12%)3=1067.67(元),所以,当债券价格低于1067.67元时,B公司才可以考虑购买。
要求:8. 计算投资A、B、C三只股票构成的投资组合的β系数和风险报酬率。
投资组合的β系数=20%×1.2+45%×1.9+35%×2=1.80
投资组合的风险报酬率=1.80×(16%-4%)=21.6%
9. 计算投资A、B、C三只股票构成的投资组合的必要报酬率。
投资组合的必要报酬率=4%+21.6%=25.6%
10. 分别计算A、B、C三只股票的必要报酬率。
A股票的必要报酬率=4%+1.2×(16%-4%)=18.4%
B股票的必要报酬率=4%+1.9×(16%-4%)=26.8%
C股票的必要报酬率=4%+2×(16%-4%)=28%
11. 分别计算A、B、C三只股票目前的市场价值。
A股票的价值=0.4/18.4%=2.17(元/股)
B股票的价值=0.6×(1+5%)/(26.8%-5%)=2.89(元/股)
C股票的价值=0.7×(1+18%)/(1+28%)+0.7×(1+18%)2/(1+28%)2+[0.7×(1+18%)2×(1+6%)/(28%-6%)]/(1+28%)2=4.11(元/股)
12. 若按照目前市价投资于A股票,估计2年后其市价可以涨到10元/股,若持有2年后将其出售,计算A股票的持有期报酬率。
假设A股票的持有期报酬率为i,则:
NPV=0.4×(P/A,i,2)+10×(P/F,i,2)-8
当i=18%,NPV=0.4×(P/A,18%,2)+10×(P/F,18%,2)-8=0.4×1.5656+10×0.7182-8=-0.19(元)
当i=16%,NPV=0.4×(P/A,16%,2)+10×(P/F,16%,2)-8=0.4×1.6052+10×0.7432-8=0.07(元)
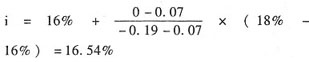
13. 若按照目前市价投资于B股票,并长期持有,计算其期望报酬率。
B股票的期望报酬率=0.6×(1+5%)/10+5%=11.3%
要求:14. 根据单期二叉树期权定价模型,计算一份该股票的看涨期权的价值。
股价上升百分比=(32-25)/25=28%,股价下降百分比=(18-25)/25=-28%

将r=5%,u=1.28,d=1-0.28=0.72,
C
u=(32-28)×100=400(元),C
d=0代入上式
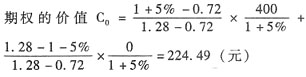
15. 假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变,若把6个月的时间分为两期,每期3个月,若该股票报酬率的标准差为0.35,计算每期股价上升百分比和股价下降百分比。

d=1-下降百分比=1/u=1/1.1912=0.8395,下降百分比=16.05%
16. 结合上一小题分别根据套期保值原理、风险中性原理和两期二叉树期权定价模型,计算一份该股票的看涨期权的价值。
①根据套期保值原理:
S
uu=25×(1+19.12%)
2=35.47(元)
S
ud=25×(1+19.12%)×(1-16.05%)=25(元)
C
uu=(35.47-28)×100=747(元)
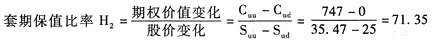
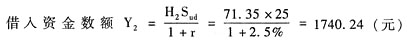
S
u=25×(1+19.12%)=29.78(元)
C
u=购买股票支出-借款=H
2S
u-Y
2=71.35×29.78-1740.24=384.56(元)
S
d=25×(1-16.05%)=20.99(元)
C
d=0
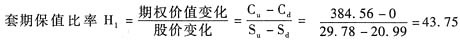
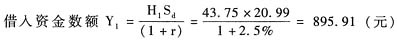
C
0=购买股票支出-借款=H
1S
0-Y
1=43.75×25-895.91=197.84(元)
| 期数
|
0
|
1
|
2
|
| 股票价格
|
25
|
29.78
|
35.47
|
|
|
20.99
|
25
|
|
|
|
17.62
|
| 期权价格
|
197.84
|
384.56
|
747
|
|
|
0
|
0
|
|
|
|
0
|
②根据风险中性原理:
期望报酬率=上行概率×股价上升百分比+下行概率×股价下降百分比=上行概率×股价上升百分比+(1-上行概率)×股价下降百分比
即:2.5%=上行概率×19.12%+(1-上行概率)×(-16.05%)
上行概率=0.5274
期权价值6个月后的期望值=0.5274×747+(1-0.5274)×0=393.97(元)
C
u=393.97(1+2.5%)=384.36(元)
期权价值3个月后的期望值=0.5274×384.36+(1-0.5274)×0=202.71(元)
期权的价值=202.71/(1+2.5%)=197.77(元)
③根据两期二叉树期权定价模型:
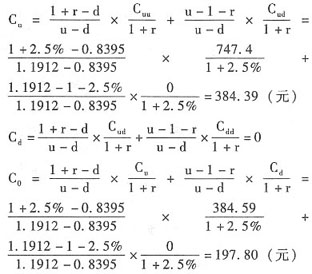
注:三种方法计算结果差异为尾数差异导致。
17. B公司是一家服装制造公司,2016年的每股销售收入为12.4元,每股收益为3.10元,每股资本支出为1元,每股折旧为0.6元。预期该公司在今后5年内高速增长,预期销售收入增长率为30%,净利润、资本支出、折旧和经营营运资本与销售收入同比例增长,β值为1.3,2016年经营营运资本为销售收入的20%。5年后公司进入稳定增长期,预期销售收入增长率为6%,即每股收益和每股经营营运资本按6%的速度增长,资本支出可以由折旧来补偿。β值为1,该公司发行在外的普通股共3000万股,长期政府债券利率为7.5%,市场平均风险溢价为5%。假设净负债比率60%可以一直保持不变。
要求:计算该公司的股权价值。
(1)估计高速成长期每股股权现金流量:股权现金流量=净利润-(资本支出-折旧)×(1-净负债比率)-经营营运资本净增加×(1-净负债比率)
每股股权现金流量2017=3.10×(1+30%)-(1-0.6)×(1+30%)×(1-60%)-[12.4×20%×(1+30%)-12.4×20%]×(1-60%)=4.03-0.21-0.30=3.52(元)
每股股权现金流量2018=3.52×(1+30%)=4.58(元)
每股股权现金流量2019=4.58×(1+30%)=5.95(元)
每股股权现金流量2020=5.95×(1+30%)=7.74(元)
每股股权现金流量2021=7.74×(1+30%)=10.06(元)
(2)估计公司高速成长期的股权资本成本:rs=7.5%+1.3×5%=14%
(3)计算公司高速成长期每股股权现金流量的现值:
公司高速成长阶段股权现金流量的现值=3.52×(P/F,14%,1)+4.58×(P/F,14%,2)+5.95×(P/F,14%,3)+7.74×(P/F,14%,4)+10.06×(P/F,14%,5)=3.52×0.8772+4.58×0.7695+5.95×0.6750+7.74×0.5921+10.06×0.5194=20.44(元)
(4)估计第6年的每股股权现金流量:
2021年每股经营营运资本=12.4×20%×(1+30%)5=9.21(元)
2022年每股经营营运资本=9.21×(1+6%)=9.76(元)
2022年经营营运资本净增加=9.76-9.21=0.55(元)
每股股权现金流量2022=3.1×(1+30%)5×(1+6%)-0.55×(1-60%)=12.20-0.22=11.98(元)
(5)计算公司稳定增长期的股权资本成本:
rs=7.5%+1×5%=12.5%
(6)计算公司稳定增长期每股股权现金流量的现值:
稳定增长期股权现金流量的现值=11.98/(12.5%-6%)×(P/F,14%,5)=95.73(元)
(7)计算公司股权自由现金流量现值总和:
V=(20.44+95.73)×3000=348510(万元)
18. 某公司2016年每股销售收入30元,每股经营营运资本10元,每股净利润6元,每股资本支出4元,每股折旧与摊销1.82元。资本结构中净负债占40%,可以保持此目标资本结构不变。
预计2017年—2021年的销售收入增长率保持在10%的水平上。该公司的资本支出、折旧与摊销、净利润与销售收入同比例增长,经营营运资本占收入的20%,可以持续保持5年。到2022年及以后股权现金流量将会保持5%的固定增长速度。
2017年—2021年该公司的β值为1.5,2022年及以后年度的β值为2,长期政府债券的利率为6%,市场组合的收益率为10%。
要求:计算该公司股票的每股价值。
单位:元
|
| 年度
|
2017年
|
2018年
|
2019年
|
2020年
|
2021年
|
| 每股净利润
|
6.6
|
7.26
|
7.99
|
8.79
|
9.67
|
| 每股销售收入
|
33
|
36.3
|
39.93
|
43.92
|
48.3l
|
| 经营营运资本
|
6.6
|
7.26
|
7.99
|
8.78
|
9.66
|
| 经营营运资本净增加
|
-3.4
|
0.66
|
0.73
|
0.79
|
0.88
|
| 资本支出
|
4.4
|
4.84
|
5.32
|
5.85
|
6.44
|
| 减:折旧与摊销
|
2
|
2.2
|
2.42
|
2.66
|
2.93
|
| 净经营资产增加
|
-1
|
3.3
|
3.63
|
3.98
|
4.39
|
| 本期股东权益增加
|
-0.6
|
1.98
|
2.18
|
2.39
|
2.63
|
| 股权现金流量
|
7.2
|
5.28
|
5.81
|
6.4
|
7.04
|
[考点] 本题的主要考核点是企业价值评估的现金流量折现法的应用。
[解析] 股权现金流量=净利润-(1-负债率)×(资本支出-折旧与摊销)-(1-负债率)×经营营运资本净增加=净利润-(1-负债率)×净经营资产增加=净利润-本期股权增加
2017年—2021年该公司的股权资本成本=6%+1.5×(10%-6%)=12%
2022年及以后年度该公司的股权资本成本=6%+2×(10%-6%)=14%

[注意] 本题直接给出的是“2022年及以后股权现金流量将会保持5%的固定增长速度”,所以,D
0×(1+g)=D
1。
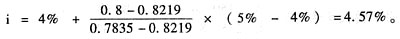
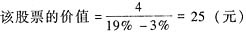
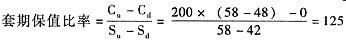


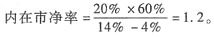

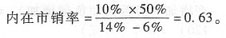
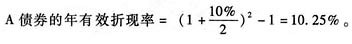


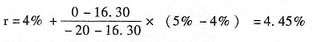
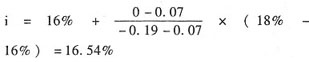

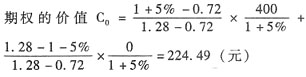

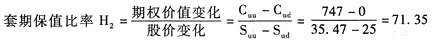
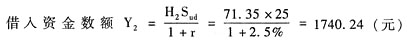
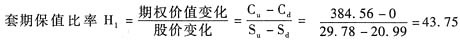
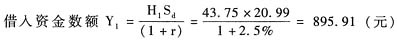
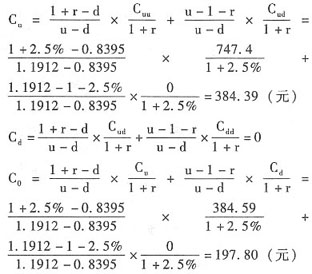



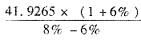 ×(P/F,8%,5)=24×0.9259+18.9×0.8573+20.79×0.7938+22.869×0.7350+41.9265×0.6806+2222.1045×0.6806=1612.6359(万元)
×(P/F,8%,5)=24×0.9259+18.9×0.8573+20.79×0.7938+22.869×0.7350+41.9265×0.6806+2222.1045×0.6806=1612.6359(万元)