一、填空题1. 运动副与一般的刚性连接的根本区别在于______。
2. 从约束数目看,______个平面高副相当于一个平面低副。
3. 某构件若已知某两点的速度和加速度,则其余点的速度和加速度可利用______法求得。
4. 在一个六杆机构中,绝对瞬心有______个。
5. 某连杆机构极位夹角为30°,若输出件工作行程需时7s,则空回行程需时______。
6. 在凸轮机构从动件常用的多项式运动规律中,______规律存在柔性冲击。
7. 在滑块行程较______的曲柄滑块机构中,往往将曲柄做成偏心轮。
8. 棘轮机构能将主动件的______运动变换成从动件的单向间歇运动。
9. 凡是反行程能够自锁的蜗杆蜗轮机构,其正行程的啮合效率必定较______。
10. 在曲柄摇杆机构的四个杆件中,______必定是最短杆。
四、计算题1. 计算下图所示机构的自由度。如有复合铰链、局部自由度、虚约束需说明。
F=3n-2P
L-P
H=3×8-2×11-1=1;如下图所示,H、J处为复合铰链、C处为局部自由度、FG杆连同两个铰链为虚约束,去掉。
2. 将下图所示杆组组合成两种形式的六杆机构(画出机构简图),并计算自由度。
3. 已知一摆动导杆机构(下图),已知L
AB=100mm,L
BC=60mm,AB连线为铅垂线,曲柄以匀角速度顺时针方向转动。
(1)以长度比例尺
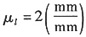
作该机构的极限位置图,并求极位夹角θ。
(2)假设ω
1=10rad/s,试用矢量方程图解法求导杆在右极限位置时的角速度ω
3和角加速度α
3(速度比例尺μ
v和加速度比例尺μ
a自行选择)。
(1)该机构的极限位置如下图a所示,极位夹角θ=φ。
(2)速度分析
取比例尺μ
v=v
B1/35=17.142
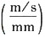
,作机构在右极限时的速度多边形,如图b所示。
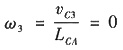
加速度分析
取比例尺μ
a=a
B1/40=0.15
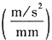
,作机构在右极限时的加速度多边形,如图c所示。
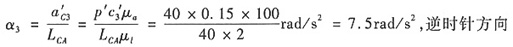
4. 如图所示刚性转子,径宽比>5,原质量m=30kg,为使圆盘平衡,在位置Ⅰ挖去质量m
1=1kg,在位置Ⅱ挖去质量m
2=0.8kg,形成两通孔,r
1=r
2=30mm。求该转子原来的不平衡质径积mr,以及原质心偏移量与偏位角α;指出现质心位置在何处。
在位置Ⅰ挖去质量m
1=1kg,在位置Ⅱ挖去质量m
2=0.8kg,相当于在反方向存在两不平衡质量,如下图所示。由偏心质量m
1产生的惯性力为
F
1=m
1r
1ω
2 由偏心质量m
2产生的惯性力为F
2=m
2r
2ω
2 刚性转子的力平衡条件为m
1r
1+m
2r
2+mr=0
取比例尺
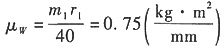
作质径积图,如图b所示。
该转子原来的不平衡质径积如图a所示,有
mr=51.22μ
W=38.415kg·mm
mr的反方向即为原不平衡质径积me的方向。
由已知m=30kg得:质心偏移量e=1.28mm,偏位角α=128.66°。
现质心位置在圆心。
5. 某曲柄摇杆机构已知部分尺寸如图所示
,曲柄AB
1和AB
2分别对应于摇杆极限位置DC
1和DC
2,试用作图法求摇杆长度L
CD、连杆长度L
BC和机架长度L
AD。
求解过程如下图所示。
由图量得:摇杆长度L
CD=34mm,连杆长度L
BC=52mm,机架长度L
AD=43mm。
6. 对于如图所示偏心圆凸轮机构(请将该机构画到答题纸上,尺寸从图上量取):
(1)画出其基圆和理论轮廓。
(2)画出此时的高副低代机构,并说出该高副低代机构的名称。
(3)问凸轮从此位置逆时针方向转多少角度后机构的压力角最大?
(4)用反转法确定在最大压力角位置时,凸轮实际轮廓上与滚子相接触点D并标出压力角α
max。
7. 如图所示轮系中,已知z
1=2(右旋蜗杆),转向如图所示,z
2=40,z
3=60,z
4=z'
4=z
5=z
6=20,z
4=100,试求传动比i
16及齿轮6的转向。
(1)分析:轮系是一个复合轮系。4-4',5、H、6,3,7为周转轮系;1、2为定轴轮系。
(2)分别列式
由定轴轮系1、2得
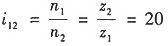
由周转轮系4-4',5、H、6,3,7得
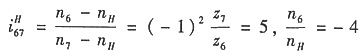
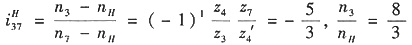
(3)联立求解,代入已知条件n
7=0,n
2=n
H,得
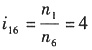
由蜗杆的转向,知蜗轮的转向箭头向上;
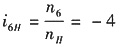
,齿轮6与行星架H转向相反(箭头向下)。
8. 1.(学术型)机构如图1所示,图中虚线为摩擦圆,滑块与导路的摩擦角为φ,F为驱动力,Q为生产阻力,试分别在图1a、b两图中画出运动副中的总反力R
12、R
32、R
41、R
43的方向。
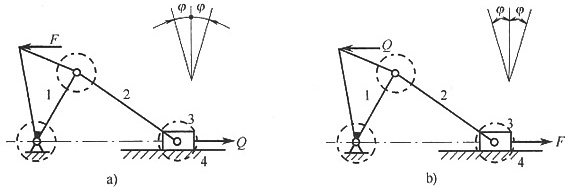 图1
图1 2.(专业型)画出图2所示机构的运动简图(尺寸不必精确)。
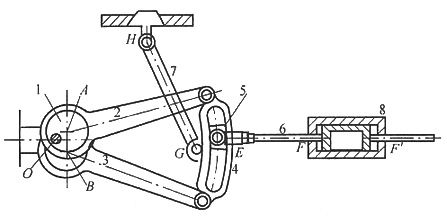 图2
图2
如图3、图4所示。
1.(学术型)
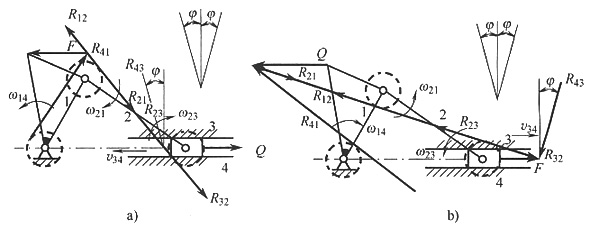 图3
图3 2.(专业型)
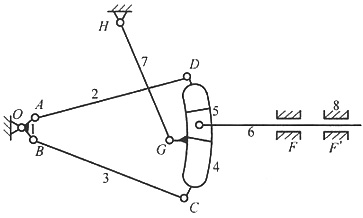 图4
图4