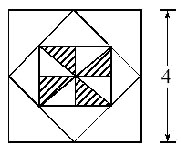
银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
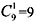 种吃法;3天吃完,有
种吃法;3天吃完,有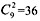 种吃法;4天吃完,有
种吃法;4天吃完,有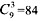 种吃法;5天吃完,有
种吃法;5天吃完,有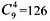 种吃法;6天吃完,有
种吃法;6天吃完,有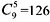 种吃法;7天吃完,有
种吃法;7天吃完,有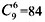 种吃法;8天吃完,有
种吃法;8天吃完,有 种吃法;9天吃完,有
种吃法;9天吃完,有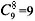 种吃法;10天吃完,有1种吃法。故共有512种不同吃法。
种吃法;10天吃完,有1种吃法。故共有512种不同吃法。
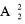 种排法;且正好间隔两辆车,从剩下的6-2=4辆车中选2辆插入甲车和乙车之间,有
种排法;且正好间隔两辆车,从剩下的6-2=4辆车中选2辆插入甲车和乙车之间,有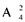 种排法,最后把剩下的两辆车排在队头和队尾有
种排法,最后把剩下的两辆车排在队头和队尾有 种排法,分步完成,所以共有
种排法,分步完成,所以共有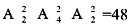 种不同的排法,选择A。
种不同的排法,选择A。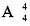 种排法,因为甲车和乙车不在队头或队尾,且正好间隔两辆车,所以只能排在第2或5位置上,有
种排法,因为甲车和乙车不在队头或队尾,且正好间隔两辆车,所以只能排在第2或5位置上,有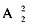 种排法,分步完成,所以共有
种排法,分步完成,所以共有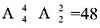 种不同的排法,选择A。
种不同的排法,选择A。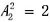 种方法,甲不和领队相邻,只能在305、306号房间,有2种方法,剩余的2人在剩余的2间房排列有
种方法,甲不和领队相邻,只能在305、306号房间,有2种方法,剩余的2人在剩余的2间房排列有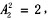 分步进行的,故有8种方法;
分步进行的,故有8种方法;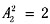 种方法,甲不和领队相邻,只能在301、306号房间,有2种方法,剩余的2人在剩余的2间房排列有
种方法,甲不和领队相邻,只能在301、306号房间,有2种方法,剩余的2人在剩余的2间房排列有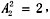 分步进行的,故有8种方法;
分步进行的,故有8种方法;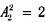 种方法,甲不和领队相邻,只能在301房间,有1种方法,剩余的2人在剩余的2间房排列有
种方法,甲不和领队相邻,只能在301房间,有1种方法,剩余的2人在剩余的2间房排列有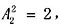 分步进行的,故有4种方法;
分步进行的,故有4种方法;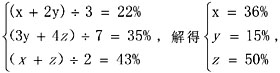 所求为(36%×5+15%×4+50%×1)÷10=29%。
所求为(36%×5+15%×4+50%×1)÷10=29%。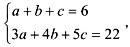 解得a-c=2,根据题意a=3,c=1,所以b=2。此题选A。
解得a-c=2,根据题意a=3,c=1,所以b=2。此题选A。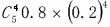


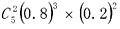

| 甲仓库 | 乙仓库 | ||||||||||||||||
| 原有 | 63 | 33 | |||||||||||||||
| 第一天 | 30 | 66 | |||||||||||||||
| 第二天 | 60 | 36 | |||||||||||||||
| 第三天 | 24 | 72 | |||||||||||||||
| 第四天 | 48 | 48 |
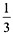 ,乙的初期投资额是丙的2倍。最终甲获得的收益比丙多2万元。则乙应得的收益为多少万元?______
,乙的初期投资额是丙的2倍。最终甲获得的收益比丙多2万元。则乙应得的收益为多少万元?______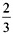 ,又乙丙投资总额占总投资的
,又乙丙投资总额占总投资的 ,则乙占总投资的
,则乙占总投资的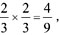 丙占
丙占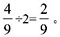 甲乙丙收益之比与投资额之比相同,为
甲乙丙收益之比与投资额之比相同,为 现已知甲比丙多收益2万元,对应收益比中的“1份”,故乙应得收益为4×2=8万元。选择C。
现已知甲比丙多收益2万元,对应收益比中的“1份”,故乙应得收益为4×2=8万元。选择C。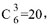 选C。
选C。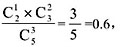 选B。
选B。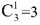 种方法;
种方法; 种方法;
种方法;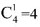 种方法。
种方法。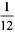 车速+人速=
车速+人速=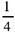
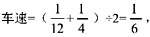 即发车间隔为6分钟。
即发车间隔为6分钟。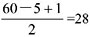 张票时能保证当选,故甲至少再得28-15=13张票。
张票时能保证当选,故甲至少再得28-15=13张票。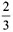 ,则小张当月工资为4500×25%×2÷
,则小张当月工资为4500×25%×2÷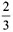 =3375元,选择A。
=3375元,选择A。 ,然后从剩下的6人中选取2人到第二个下级单位去,记作
,然后从剩下的6人中选取2人到第二个下级单位去,记作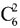 。分步用乘法
。分步用乘法
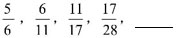
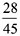
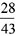
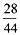
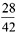
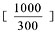 ×100+280=1580元, [ ]内数字取整数部分。
×100+280=1580元, [ ]内数字取整数部分。 ×100%≈1280÷1600=80%,相当于打了八折。答案为D。
×100%≈1280÷1600=80%,相当于打了八折。答案为D。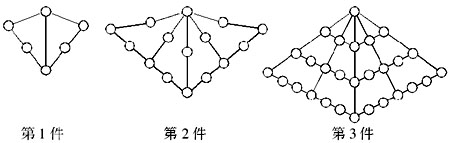
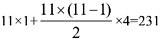 颗。
颗。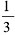 ,第二个人中奖几率为(1-
,第二个人中奖几率为(1-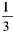 )×
)×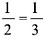 ,第三个人中奖几率为
,第三个人中奖几率为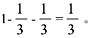 所以一样大。
所以一样大。