一、填空题1. 经过动平衡的转子一定能保证静平衡,这是因为______。
2. 衡量转子平衡优劣的指标有______,______。
3. 刚性转子平衡精度A的表达方式是______。
4. 符合静平衡条件的回转构件,其质心位置在______;静不平衡的回转构件,由于重力矩的作用,必定在______位置静止,由此可确定应加上或除去平衡质量的方向。
5. 刚性转子静平衡的力学条件是______,而动平衡的力学条件是______。
6. 平面连杆机构惯性力的平衡条件是______。
通过机构质心的总惯性力F和总惯性力偶矩M分别为零(F=0,M=0)
7. 用假想的集中质量的惯性力及惯性力矩来代替原机构的惯性力及惯性力矩,该方法称为______。
8. 回转体的不平衡可分为两种类型,一种是______,其质量分布特点是______;另一种是______,其质量分布特点是______。
静不平衡 在同一回转面上 动不平衡 不在同一回转面上
9. 作转子静平衡时,应选______个平衡平面;而动平衡时,应选______个平衡平面。
10. 研究机械平衡的目的是部分或完全消除构件在运动时所产生的______,减小或消除在机构各运动副中所引起的______,减轻有害的机械振动,改善机构工作性能和延长使用寿命。
11. 回转构件进行平衡时,应在______加(或减)平衡质量,平衡试验方法有______、______。
12. 机构总惯性力在机架上平衡的条件是平面机构总质心______。
13. 对于绕固定轴回转的构件,可以采用______或______的方法,使构件上所有质量的惯性力形成平衡力系,达到回转构件的平衡。若机构中存在作往复运动或平面复合运动的构件,则应采用______或______方法,方能使作用在机架上的总惯性力得到平衡。
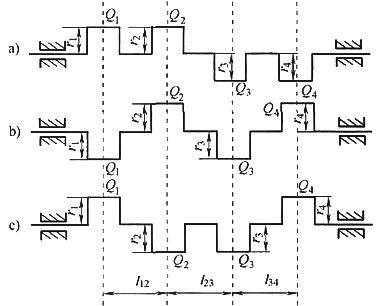
15. 如图所示a、b、c三根曲轴,已知Q
1=Q
2=Q
3=Q
4,r
1=r
2=r
3=r
4=r,L
12=L
23=L
34=l,其中______轴已达到静平衡,而______既达到静平衡又达到动平衡。
16. 具有______的等效构件的动能等于原机构的动能,而作用于其上的______瞬时功率等于作用在原机构上的所有各外力在同一瞬时的功率。
17. 机器产生速度波动的主要原因是______。速度波动的类型有______和______两种。前者一般采用的调节方法是______,后者一般采用的调节方法是______。
输入功不等于输出功 周期性 非周期性 飞轮 调速器
18. 计算等效力(或力矩)的条件是______;计算等效转动惯量(或质量)的条件是______。
20. 在电动机驱动的冲床上加了飞轮之后,选用的电机功率比原先的______。
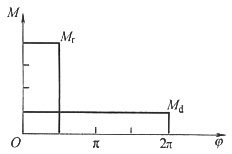
21. 如图所示为某机器的等效驱动力矩M
d(φ)和等效阻力矩M
r(φ)的线图,其等效转动惯量为常数,该机器在主轴位置角φ等于______时,主轴角速度达到ω
max,在主轴位置角φ等于______时,主轴角速度达到ω
min。
2π
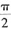
22. 用飞轮进行调速时,若其他条件不变,则要求的速度不均匀系数越小,飞轮的转动惯量将越______,在满足同样的速度不均匀系数条件下,为了减小飞轮的转动惯量,应将飞轮安装在______轴上。
23. 在建立机械系统的等效动力学模型时,其等效的条件是______和______;等效力和等效质量与机构的真实运动速度的大小______。
24. 机器等效动力学模型中的等效质量(转动惯量)是根据系统总动能______的原则进行转化的,因而它的数值除了与各构件本身的质量(转动惯量)有关外,还与构件的______有关。
25. 当机器中仅包含速比为______机构时,等效动力学模型中的等效质量(转动惯量)是常数;当机器中包含______自由度的机构时,等效质量(转动惯量)是机构位置的函数。
26. 若已知机械系统的盈亏功为ΔW
max,等效构件的平均角速度ω
m,系统许用速度不均匀系数为[δ],未加飞轮时,系统的等效转动惯量的常量部分为J
e,则飞轮转动惯量J
F≥______。
27. 若不考虑其他因素,单从减轻飞轮的重量上看,飞轮应安装在______轴上。
28. 若机构中的所有构件作______运动,则等效构件上的等效转动惯量或等效质量与机构位置无关;在计算等效转动惯量或等效质量时______知道机器的真实运动。
29. 机器作变速稳定运转的条件是______,其运转不均匀系数δ可表达成______。
在J和M的公共周期内驱动功等于阻抗功 δ=(ωmax-ωmin)/ωm
四、计算题1. 如图所示盘状转子上有两个不平衡的质量:m
1=1.5kg,m
2=0.8kg,r
1=140mm,r
2=180mm,相位如图所示。现用去重法来平衡,求所需挖去的质量的大小和相位(设挖去质量处的半径r
b=140mm)。
m
1r
1=1.5×0.14=0.21kg·m,m
2r
2=0.8×0.18=0.144kg·m
m
1r
1+m
2r
2+m
br
b=0
取
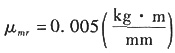
画惯性力矢量多边形,如下图所示。
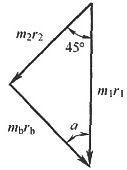
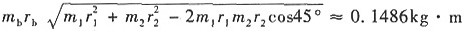
m
b=1.061kg
α=arcsin(m
2r
2sin45°/m
br
b)=43.26°
在图上轴心左上方与垂线成43.26°的140mm半径处挖去1.061kg质量。
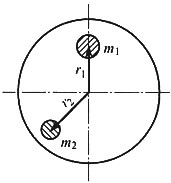
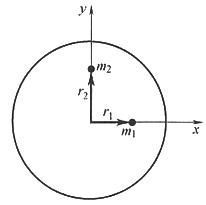
2. 如图所示圆盘绕O点旋转。若已知圆盘上的平衡质量m
b=0.06kg,平衡半径r
b=50mm,不平衡质量m
1=0.2kg,不平衡半径r
1=20mm;不平衡质量m
2=0.25kg,试求r
2的大小和方位。又问:若圆盘转速为1000r/min,在未加平衡质量前,轴承处动反力为多大?
m
br
b=3kg·mm,m
1r
1=4kg·mm,m
br
b+m
1r
1+m
2r
2=0
取
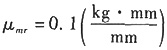
画质径积矢量多边形,如下图所示。
m
2r
2=5kg·mm
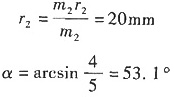
r
2与Y轴成126.9°。
轴承处动反力
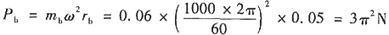
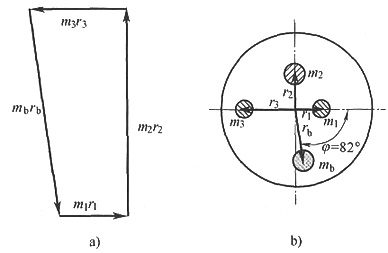
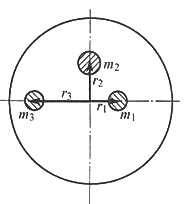
3. 如图所示盘形回转件上存在三个偏置质量,已知m
1=10kg,m
2=15kg,m
3=10kg,r
1=50mm,r
2=100mm,r
3=70mm,设所有不平衡质量分布在同一回转平面内,问应在什么方位上加多大的平衡质径积才能达到平衡?
这是一个刚性转子的静平衡问题。
各偏心质量的质径积分别为
m
1r
1=10×50kg·mm=500kg·mm
m
2r
2=15×100kg·mm=1500kg·mm
m
3r
3=10×70kg·mm=700kg·mm
平面汇交力系的平衡条件
m
1r
1+m
2r
2+m
3r
3+m
br
b=0
取比例尺
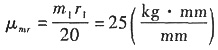
作质径积多边形图,如下图a所示。
m
br
b=60.02×μ
mr=1501kg·mm
取r
b=100mm,m
b=15.01kg,方位角φ=82°,如图b所示。
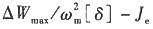
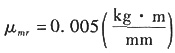 画惯性力矢量多边形,如下图所示。
画惯性力矢量多边形,如下图所示。
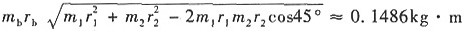
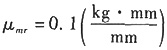 画质径积矢量多边形,如下图所示。
画质径积矢量多边形,如下图所示。
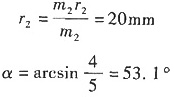
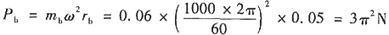
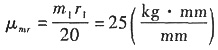 作质径积多边形图,如下图a所示。
作质径积多边形图,如下图a所示。