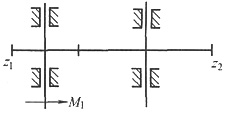
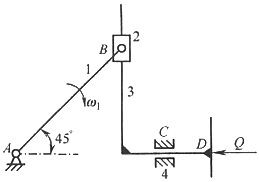
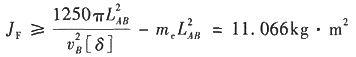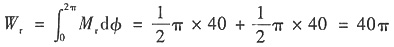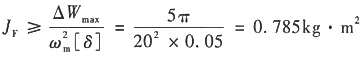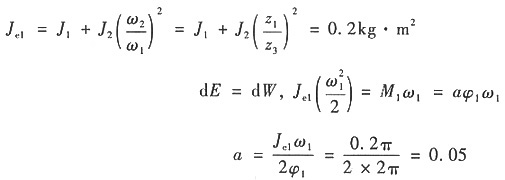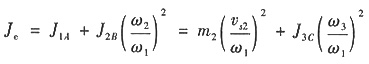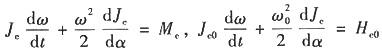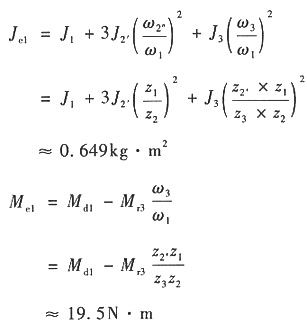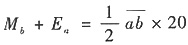一、填空题1. 槽轮机构运动系数k的取值范围是______。
2. 在齿式棘轮机构中,为保证棘爪能顺利进入棘轮轮齿的根部,应满足的条件是______。
3. 棘轮的标准模数m等于棘轮的______直径与齿数z之比。
5. 槽轮机构是由______、______、______组成的。对于原动件转一周,槽轮只运动一次的槽轮机构来说,槽轮的槽数应不小于______;槽轮机构的运动特性系数总小于______。
6. 槽轮机构中,为避免刚性冲击,设计时应保证______。
7. 一外槽轮机构,其槽数z=4,拨盘上有一个拨销,则该机构的运动系数k=______。
8. 在单万向铰链机构中,主、从动轴传动比i
31=ω
3/ω
1的变化范围是______,其变化幅度与______有关。
9. 欲将一构件的匀速回转运动转换成从动件的单向间歇回转运动,可采用______、______、______机构。
四、计算题1. 有一外啮合槽轮机构,槽轮的槽数z=6,槽轮运动时间和停歇时间分别为2s和1s。求该机构运动系数及所需的圆销数目。
k=td/t=2/3
k=n(1/2-1/z),n=2
2. 某装配工作台有六个工位,每个工位在工作静止时间t
j=10s内完成装配工序。转位机构采用单销外槽轮机构。试求:
(1)该槽轮机构的运动系数k。
(2)主动件拨盘的转速ω
1。
(3)槽轮的转位时间t
d。
(1)因工作台为六工位,所以槽轮槽数z=6。
k=td/t=1/2-1/z=1/3
(2)由k=td/t=(t-tj)=1/3得
t=15s,ω=2π/t=0.419rad/s
(3)td=t-tj=5s
3. 某牛头刨床工作台的横向进给丝杠,已知其导程l=5mm,与丝杠轴联动的棘轮齿数z=40,问棘轮的最小转动角度和该刨床的最小横向进给量各为多少?
棘轮最小转动角δ=360°/z=9°
该刨床最小横向进给量

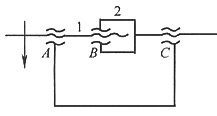
4. 如图所示螺旋机构中,螺旋A、B、C均为右旋,导程分别为l
A=6mm,l
B=6mm,l
C=6mm。试求当构件1按图示方向转一圈时,构件2的轴向位移s
2及转角φ
2。
因螺旋副均为右旋,所以螺杆1转一圈时,若构件2不转动,其相对位移s'2=lA-lB,方向向右;构件2同时还有转动,转动方向应与构件1转动方向相反,设转角为φ2,其相对机架位移s2=lCφ22π,方向向左;转角φ2引起构件2相对构件1的位移为lBφ22π,方向向左。
s2=lCφ22π=(lA-lB)-LBφ2/2π
φ2=2π(lA-lB)/(lC+lB)=π/5 与n1反向,
s2=lCφ22π=2.4mm 方向向左。
5. 如图所示为一微动调节的差动螺旋机构,构件1与机架3组成螺旋副A,其导程l
A为2.8mm,右旋。构件2与机架3组成移动副C,2与1还组成螺旋副B,现要求当构件1转一圈时,构件2向右移动0.2mm,问螺旋副B的导程l
B为多少?右旋还是左旋?
由s2=lB-lA=0.2得:lB=3.0mm;螺旋副B为右旋。
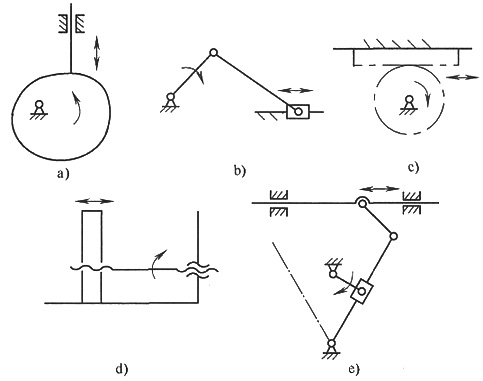
6. 在机电产品中,一般均采用电动机作为动力源,为了满足产品的运动要求,经常需要把电动机输出的旋转运动进行变换(例如改变转速的大小和方向,或改变运动形式),以实现产品所要求的运动形式。现要求把电动机的旋转运动变换为直线运动,请列出5种实现该运动变换的传动形式,并画出机构示意图。若要求机构的输出件能实现复杂的直线运动规律,则该采用何种传动形式?
五种传动机构形式为:
1)直动从动件盘形凸轮机构(尖顶、滚子、平底均可)(下图a)。
2)曲柄滑块机构(下图b)。
3)齿轮齿条机构(下图c)。
4)螺旋传动机构(下图d)。
5)摆动导杆滑块机构(下图e)。
若要求输出件实现复杂的直线运动规律,应选用移动从动件盘形凸轮机构。
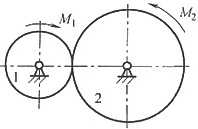
7. 如图所示齿轮机构,z
1=20,z
2=40,J
1=0.01kg·m
2,J
2=0.04kg·m
2,作用在齿轮1上的驱动力矩M
1=10N·m,齿轮2上的阻力矩M
2=4N·m,齿轮2以角速度ω
2从零等加速上升到100rad/s时,所需的时间t为几秒?
选取齿轮2为等效构件,则等效转动惯量
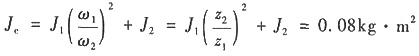
等效力矩
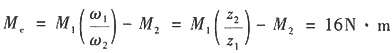
因为J
eα=M
e,所以
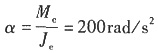
,则
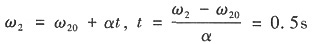
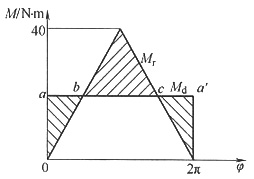
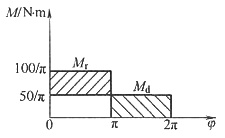
8. 一机组主轴在稳定运动循环中等效驱动力矩M
d和等效阻力矩M
r变化曲线如图所示,各块面积值见下表,单位:N·m。主轴的平均转速n
m=800r/min,许用运动不均匀系数[δ]=0.02,忽略其他构件的质量。求:
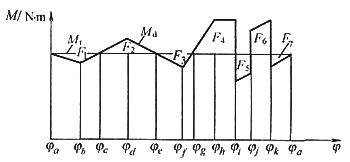
(1)需装在主轴上飞轮的转动惯量J
F。
(2)主轴在哪个位置角转速最高?最高转速n
max为多少?
| F1 | F2 | F3 | F4 | F5 | F6 | F7 |
| 340 | 810 | 600 | 910 | 555 | 470 | 695 |
(1)Ee=Ea-F1=Ea-340N·m,Ee=Ee-F2=Ea+470N·m
Eg=Ee-F3=Ea-130N·m,Ei=Eg+F4=Ea+780N·m
Ej=Ek-F5=Ea+225N·m,Ek=Ei+F6=Ea+659N·m
Ea=Ek-F7=Ea(N·m)
ΔWmax=Emax-Emin=ΔEi-ΔEe=1120N·m
(2)mn=(nmax+nmin)/2,nmax+nmin=1600r/min
δ=(nmax-nmin)/nm,nmax-nmin=nmδ=16r/min
得nmax=808r/min
主轴在φ转角处动能最大,转速最高。
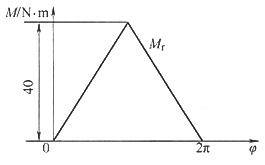
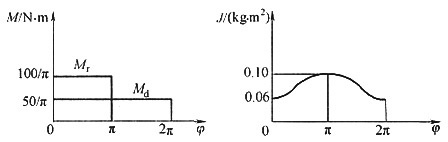
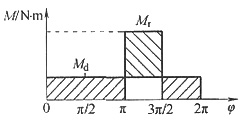
9. 某机器的主轴为等效构件,等效驱动力矩、等效阻抗力矩和等效转动惯量的变化规律如图所示。
(1)判断该机器能否作周期性的变速稳定运转,说明理由。
(2)在运转周期的初始位置,φ=0,ω
0=100rad/s,求出主轴的最大角速度ω
max与最小角速度ω
min的值及其对应的转角位置。
如下图所示。
(1)在一个运动周期(2π)内

W
d=W
r,即在一个周期的始末,驱动功等于阻抗功,动能增量为零(ΔE=0),故该机器能够作周期性变速稳定运转。
(2)机器在φ=0时的动能
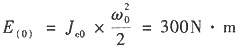
在φ=π时的动能

在φ=2π时的动能
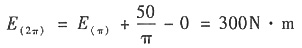
因此,机器主轴转角为0及2π时,动能最大;主轴转角为π时动能最小。又由题中J-φ图知,主轴转角为0及2π时,转动惯量J最小;主轴转角为π时,转动惯量J最大。
由
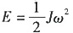
得
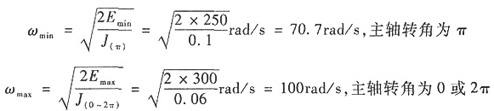
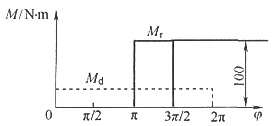
10. 一机器作稳定运转,其中一个运动循环中的等效驱动力矩M
d和等效阻力的M
r的变化如图所示。机器的等效转动惯量J=1kg·m
2,在运动循环开始时,等效构件的角速度ω
0=100rad/s,试求:
(1)等效构件的最大、最小角速度ω
max和ω
min。
(2)机器运转速度不均匀系数δ。
(1)如下图所示
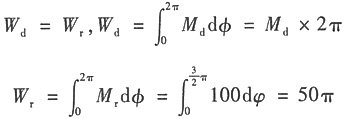
所以M
d=25N·m
等效构件在各位置角时的动能:
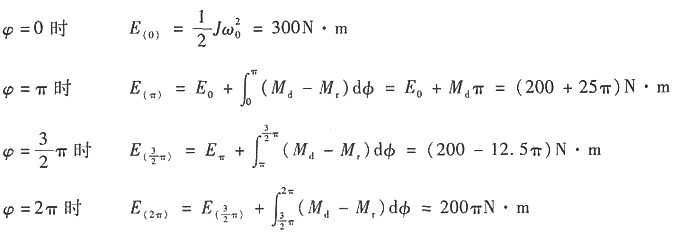
等效构件转角为π时,能量最大;而在
时,能量最小。
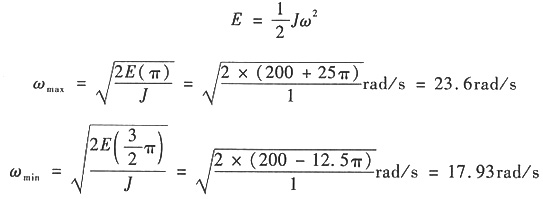
(2)
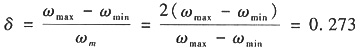
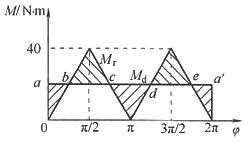
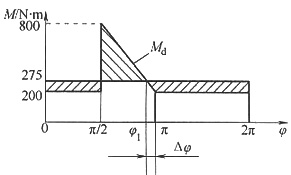
11. 如图所示为作用在机器主轴上一个工作循环内驱动力矩M
d的变化规律。设阻力矩M
r为常数,平均转速n
m=1000r/min,试求
(1)阻力矩M
r。
(2)最大盈亏功ΔW
max。
(3)若速度不均匀系数为δ=0.05,应装在主轴上飞轮的转动惯量J
F。
(1)W
d=W
r 
W
r=W
r×2π
阻力矩W
r=W
d/2π=275N·m
(2)如下图所示,
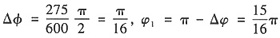
设主轴转角φ=0的动能为E
0,则

△W
max=E
max-E
min=114.844πN·m=360.8N·m
(3)J
F≥ΔW
max/(

[δ])=900ΔW
max/(π
2n
2[δ])≈0.66kg·m
2
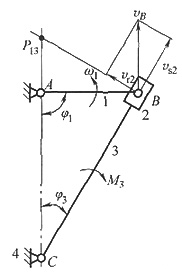
12. 如图所示导杆机构中,已知L
AB=100mm,加在导杆3上的力矩M
3=100N·m,导杆对轴C的转动惯量J
B=0.0006kg·m
2,试求:
(1)当φ
1=90°,φ
3=30°时,由M
3转化到构件1上的等效阻矩M
er及转化到轴A的等效转动惯量J
e1。
(2)当∠ABC=90°时,转化到轴A上的等效转动惯量J
e1及阻力矩M
er。
如下图所示。
(1)构件1、3的瞬心P
13为过B点的BC垂线与CA延长线交点。
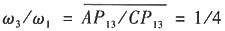
,M
er=M
3ω
3/ω
1=25N·m
J
e1=J
s(ω
3/ω
1)=0.006×
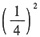
=0.000375kg·m
2 (2)当∠ABC=90°时,ω
3=0,M
er=0,J
e1=0。
13. 正弦机构的位置如图所示。已知:作用在构件3上阻力Q=400N,构件1的角速度ω
1=10rad/s。长度比例尺
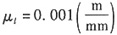
。
(1)试用瞬心法构件3上D点的速度。
(2)若以构件1为等效构件,试求该瞬时位置机构的等效阻力矩M
r。
如下图所示。
(1)P
14在A点,P
12在B点,P
23在过B点的导轨垂线上无穷远处,P
34在导轨垂线上无穷远处,P
13在P
14P
34与P
12P
23交点处。
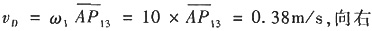
(2)M
r=Q(cos180°)(v
D/ω
1)=15.2N·m
14. 如图所示,将机组的力和质量都等效到曲柄AB上的B点。在机组稳定运动时,它的一个运动循环对应于轴的一转。已知切向等效阻力F
r是点曰行程S
B的函数,即F
r=F
r(S
B)(如图所示);切向等效驱动力F
d在稳定运动中为常数;机组各构件质量的等效质量m=150kg为常量;等效点的平均速度v
B=2.5m/s;曲柄的长度L
AB=100mm。求:
(1)保证不均匀系数δ≤0.05的飞轮转动惯量J
F。
(2)飞轮的最大角加速度α
max。
(1)W
d=W
r 
设a点处动能为E
a,则
E
b=E
A+ΔW
1=E
a+

×5000=(E
a+625x)N·m
E
c=E
b-ΔW
2=(E
a-625x)N·m,E
d=E
c+ΔW
3=(E
a+312.5x)N·m
E
e=E
d-ΔW
4=(E
a-312.5x)N·m,E
f=E
e+ΔW
5=(E
a-312.5x)N·m
E
g=E
f-ΔW
6=(E
a-312.5x)N·m,E'
a=E
g-ΔW
7=0
ΔW
max=E
max-E
min=E
b-E
c=1250xN·m
因为

其中

所以
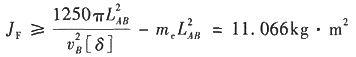
(2)α=M/J,M
max=(F
d-F
rmin)L
AB,J=J
F+J
e 
15. 某机械在稳定运动的一个周期中,作用在等效构件上的等效阻力矩M
r的变化规律如图所示,等效驱动力矩M
d为常数,平均角速度ω
m=20rad/s,要求运转速度不均匀系数δ=0.05,忽略除飞轮以外构件的等效转动惯量。试求:
(1)等效驱动力矩M
d。
(2)最大盈亏功ΔW
max。
(3)应在等效构件上安装的飞轮转动惯量J
F。
如下图所示。
(1)因为W
d=W
r,W
d=W
d×2π
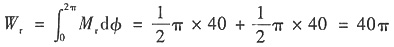
所以W
d=20N·m
(2)设a点的动能为E
a,则

△W
max=E
max-E
min=5π
(3)
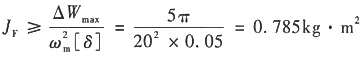
16. 如图所示的一对齿轮传动中,齿数z
1=30,z
2=60,转动惯量J
1=0.1kg·m
2,J
2=0.4kg·m
2,齿轮1上受驱动力矩M
1=aφ
1,其中a为比例常数,φ
1为齿轮1转角。已知该对齿轮由静止起动,当轮1转过1周时,其角速度ω
1=πrad/s,求a。
以齿轮1为等效构件
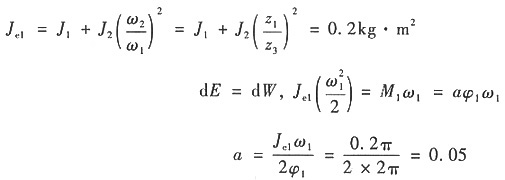
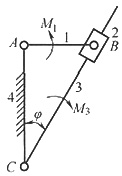
17. 如图所示为导杆机构的起动装置,已知φ=30°,J
1A=0.12kg·m
2,J
2B=0.12kg·m
2,m
2=1kg,J
3C=0.2kg·m
2,M
1=5N·m,M
3=8N·m,L
AB=0.1mm。求在起动瞬时,杆1的角加速度α
1的大小和方向。(A、B、C分别是构件1、2、3的质心)。
由上图得

取杆1为等效构件
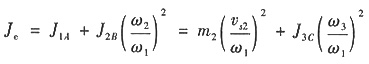
其中

起动时

等效力矩

起动瞬时t=0,ω
0=0
由
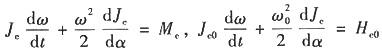
即J
e0α
1=M
e0 则α
1=M
e0/J
e0=3/0.1475rad/s
2=20.34rad/s
2 其方向与M
1方向一致(逆时针方向)。
18. 如图所示为一起重装置。蜗杆为右旋,蜗杆头数z
1,蜗轮齿数z
2。轴Ⅰ组件的转动惯量为J
1,轴Ⅱ组件的转动惯量为J
2,重物的重量为G,卷筒直径为D。
(1)试确定提升重物时,蜗杆的转向。
(2)设施加在轴Ⅰ上的驱动力矩为常数M
d,不计运动副和蜗杆蜗轮啮合的摩擦,要使重物在ts内,由静止达到上升速度v,试确定M
d的大小。
(1)提升重物,蜗轮转向箭头向上,右旋蜗杆的转向应为逆时针方向。
(2)选Ⅱ轴为等效构件

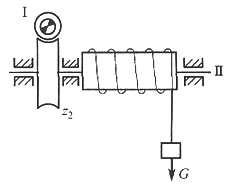
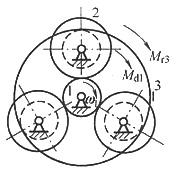
19. 如图所示为一齿轮减速装置。已知各齿轮的齿数分别为:z
1=z
2'=20,z
2=40,z
3=80,齿轮1的转动惯量J
1=0.196kg·m
2。齿轮2与2'为双联齿轮,其数量k=3,每一对双联齿轮对其轴心的转动惯量J
22'=0.588kg·m
2,内齿轮3的转动惯量J
3=0.78kg·m
2。作用在齿轮1上有常值驱动力矩M
d1=98.1N·m,而齿轮3上作用有常值阻力矩M
r3=941N·m。若选齿轮1为等效构件,试确定该机构的等效转动惯量J
e1和等效力矩M
e1。
20. 某机械在转化构件上作用的等效阻力矩M
r,在一个工作循环中的变化规律如图所示,等效驱动力矩M
d为常数,试求:
(1)等效驱动力的值。
(2)最大盈亏功。
如下图所示。
(1)

可得M
d=20N·m
(2)设a点处机械的动能为E
a,则


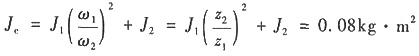
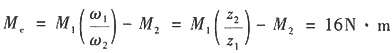
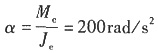 ,则
,则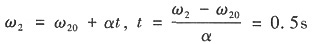


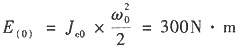

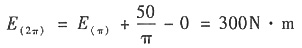
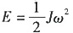 得
得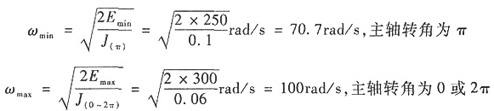
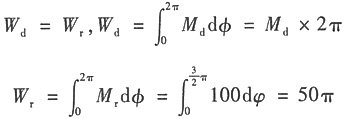
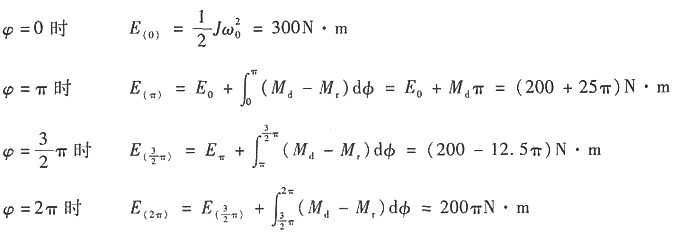 等效构件转角为π时,能量最大;而在
等效构件转角为π时,能量最大;而在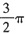 时,能量最小。
时,能量最小。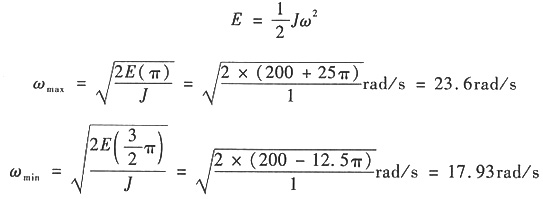
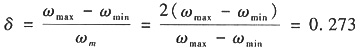


 [δ])=900ΔWmax/(π2n2[δ])≈0.66kg·m2
[δ])=900ΔWmax/(π2n2[δ])≈0.66kg·m2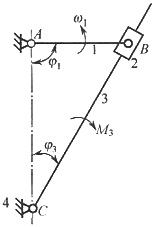
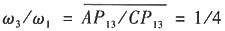 ,Mer=M3ω3/ω1=25N·m
,Mer=M3ω3/ω1=25N·m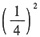 =0.000375kg·m2
=0.000375kg·m2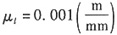 。
。

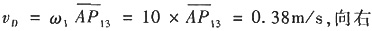


 ×5000=(Ea+625x)N·m
×5000=(Ea+625x)N·m