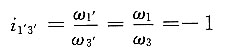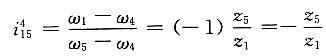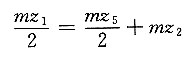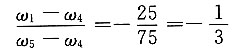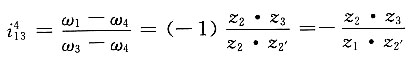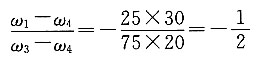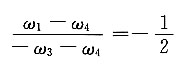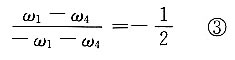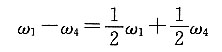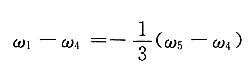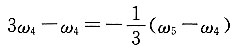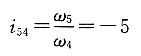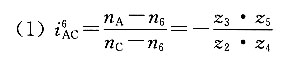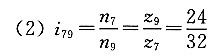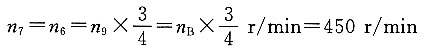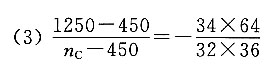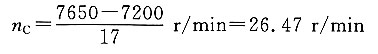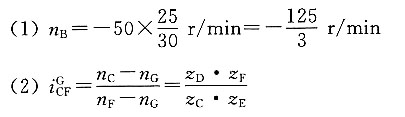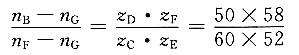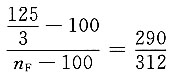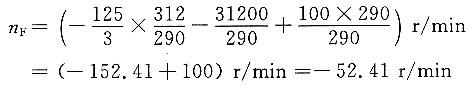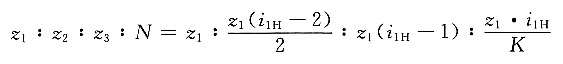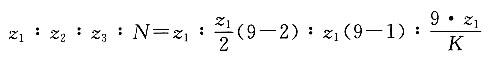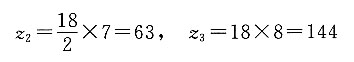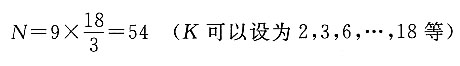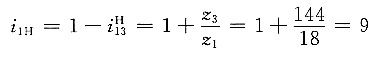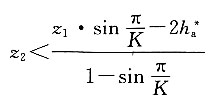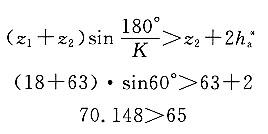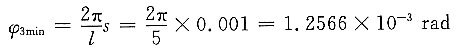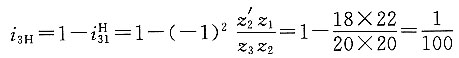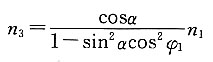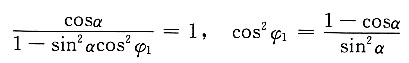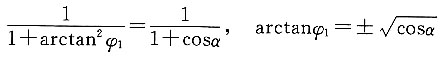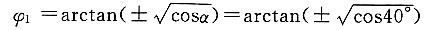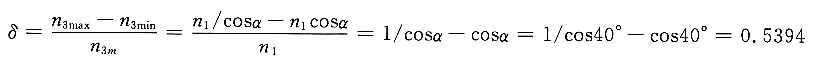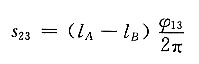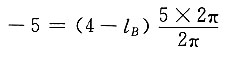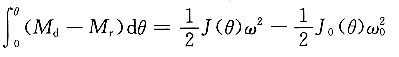计算题1. 求如图所示轮系的传动比i
14,已知z
1=z
2'=25,z
2=z
3=20,z
H=100,z
4=20。
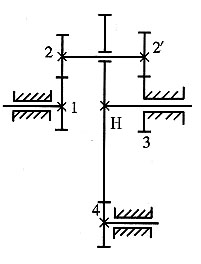
解题要点: (1)图示为一复合轮系。
(2)由齿轮1、2、2'、3和行星架H组成行星轮系,其传动比为
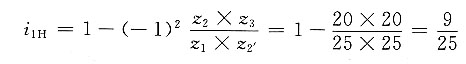
(3)由齿轮4和行星架H组成定轴轮系,其传动比为
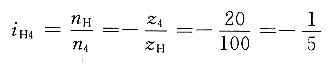
(4)传动比
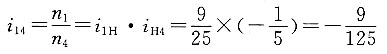
齿轮1和齿轮4的转向相反。
2. 在如图所示的轮系中,各齿轮均为标准齿轮,并已知其齿数分别为z
1=34,z
2=22,z
4=18,z
5=35。试求齿数z
3及z
6,并计算传动比i
1H2。

解题要点: (1)图示轮系为一复合轮系,由两个周转轮系组合而成。
(2)求齿数z
3、z
6。
z
3=z
1+2z
2=34+2×22=78
z
6=z
4+2z
5=18+2×35=88
(3)由齿轮1、2、3及行星架H。组成行星轮系。
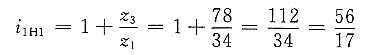
(4)由齿轮4、5、6及行星架H
2组成行星轮系。
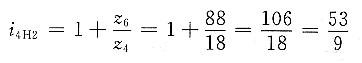
(5)求i
1H2。
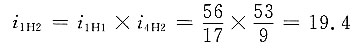
3. 求如图所示卷扬机减速器的传动比i
1H。若各轮的齿数为z
1=24,z
2=48,z
2'=30,z
3=60,z
3'=20,z
4=40,z
4'=100。
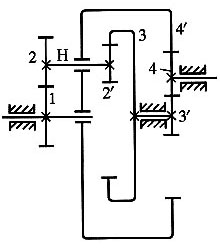
解题要点: (1)图示轮系为一复合轮系,由齿轮1、2、2'、3和行星架H组成差动轮系;由齿轮3'、4、4'组成定轴轮系。
(2)定轴轮系的传动比为
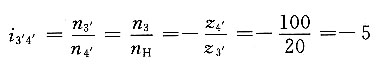
所以 n
3=-5n
H (3)差动轮系的转化机构的传动比为
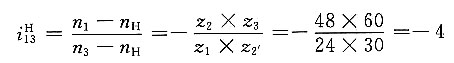
(4)由上式得 n
1-n
H=4n
H-4n
3 n
1=5n
H-4n
3=5n
H-4(-5n
H)=25n
H 所以
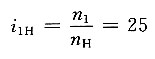
齿轮1与卷扬机筒的转向相同。
4. 在如图所示的电动三爪卡盘传动轮系中,已知各轮齿数为z
1=6,z
2=z
2'=25,z
3=57,z
4=56,试求传动比i
14。
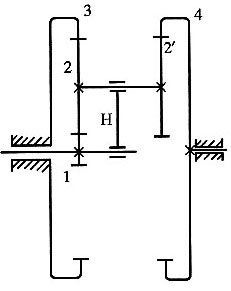
解题要点: (1)三爪卡盘传动轮系是一个行星轮系,它可以看做由两个简单的行星轮系组成。第一个行星轮系由齿轮1、2、3和行星架H所组成;第二个行星轮系由齿轮3、2、2'、4和行星架H组成。
(2)这两个行星轮系通过双联行星齿轮(2和2')复合在一起。
(3)第一个行星轮系的传动比为
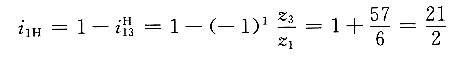
(4)第二个行星轮系的传动比为
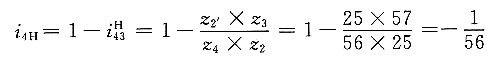
(5)所求传动比为
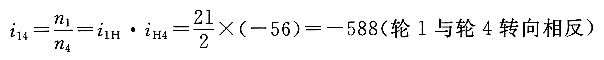
5. 在如图所示的轮系中,轮1与电动机轴相连,n
1=1440r/min,z
1=z
2=20,z
3=60,z
4=90,z
5=210,求n
3=?
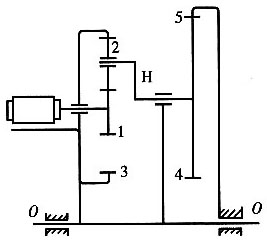
解题要点: (1)给整个轮系一个一n
3绕OO轴线转动,构件3就转化成为固定构件。此时,该轮系为一复合轮系,并由两部分组成。
(2)1-2-3-H转化为普通行星轮系
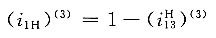
即
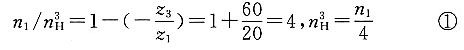
(3)轮4、5转化为定轴轮系,有
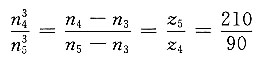
由于n
4=n
H,n
5=0,上式化为
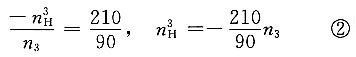
(4)将①、②两式联立求解,得
n
3=-90n
1/(4×210)=-154.29r/min
轮3与电动机转向相反。
6. 在如图所示的轮系中,设各轮的模数均相同,且为标准传动,若已知其齿数z
1=z
2'=z
3'==z
6'=20,z
2=z
4=z
6=z
7=40,试问:
(1)齿轮3、5的齿数应如何确定?
(2)当齿轮1的转速n
1=980r/min时,齿轮3、5的运动情况各如何?
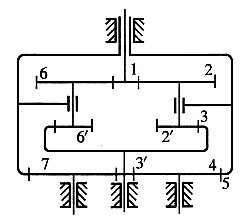
解题要点: (1)确定齿数。
根据同轴条件,可得
z
3=z
1+z
2+z
2'=20+40+20=80
z
5=z
3'+2z
4=20+2×40=100
(2)计算齿轮3、5的转速。
①图示轮系为封闭式轮系,在作运动分析时应划分为如下两部分来计算。
②在1-2(2')-3-5组成的差动轮系中:
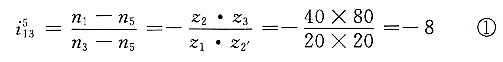
③在3'-4-5组成的定轴轮系中:
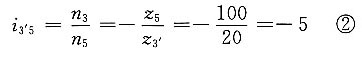
④联立式①及式②,得
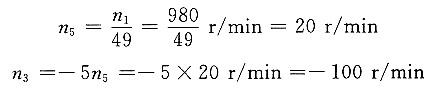
故n
3与n
1反向,n
5与n
1同向。
7. 用于自动化照明灯具上的一周转轮系如图所示。已知输入轴转速n
1=19.5r/min,组成轮系的各齿轮均为圆柱直齿轮。各轮齿数为:z
1=60,z
2=z
2'=30,z
3=40,z
4=40,z
5=120。试求箱体的转速。
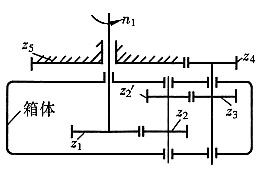
解题要点: (1)

(2)n
1-n
H=-2×(n
5-n
H)
19.5-n
H=2n
H 所以
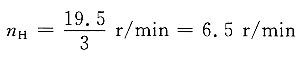
箱体的转向与n
1的转向相同。
8. 如图所示为THK6355型数控自动换刀镗床的刀库转位装置。齿轮4与刀库连接成一体,内齿轮3与机架固联,各轮齿数为:z
1=24,z
2=z
2'=28,z
3=80,z
4=78(变位齿轮)。试计算油马达与刀库间的转速关系。
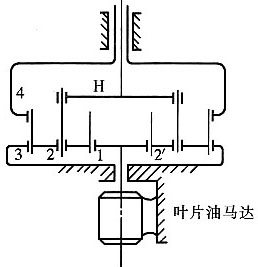
解题要点: 
9. 在如图所示的双重周转轮系中,已知各轮的齿数,试求其传动比i
1H。
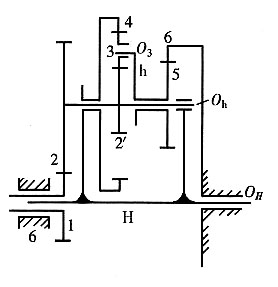
解题要点: (1)双重周转轮系的特点是它的主周转轮系的行星架内有一个副周转轮系,因此至少有一个行星轮同时绕着三个轴线转动。
(2)图示的双重周转轮系包含了两个主周转轮系(行星轮系5-H-6和差动轮系1-2-H-6,它们共有一个行星架H)和一个副周转轮系(差动轮系2'-3-4-h-6)。行星轮3同时绕三个轴线O
3、O
h及O
H转动。
(3)对于行星轮系5-H-6,有
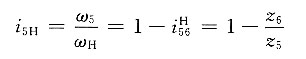
(4)对于差动轮系1-2-H-6,有
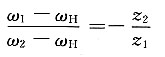
即
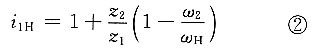
(5)对于差动轮系2'-3-4-h-6,有
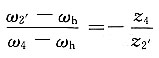
因ω
2'=ω
2,ω
h=ω
5及ω
4=ω
H,故上式可写成
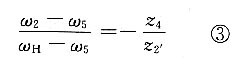
(6)将式①代入式③得
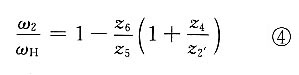
(7)再将式④代入式②得
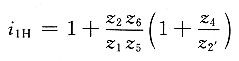
10. 在如图所示的轮系中,已知各齿轮的齿数分别为z
1=28,z
2=78,z
4=24,z
6=80,若已知n
1=2000r/min。当分别将轮3或轮6刹住时,试求行星架的转速n
H。
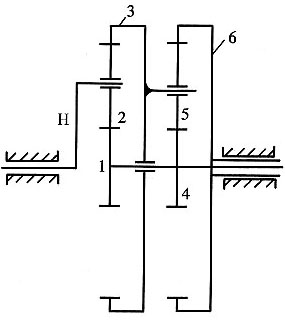
解题要点: (1)当轮3被刹住时
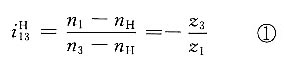
因n
3=0,得
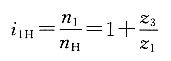
所以
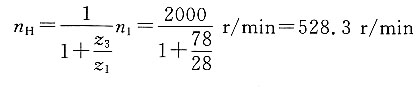
(2)当轮6被刹住时
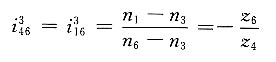
因n
6=0,得
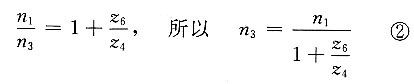
(3)将式②代入式①得
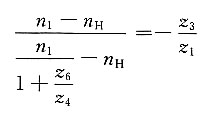
(4)解上式得
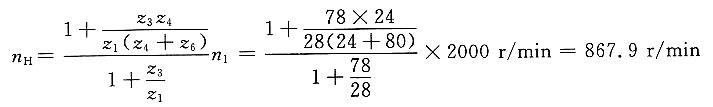
11. 在如图所示的轮系中,已知z
5=z
2=25,z
2'=20且各轮模数相同,求传动比i
54。
解题要点: (1)区分基本轮系。
先区分周转轮系,再区分定轴轮系。
①由1-2-2'-3-4组成差动轮系。
②由1-2-5-4组成差动轮系。
③由5-2-2'-3-4组成差动轮系。
④由齿轮1'-6-3'组成定轴轮系。
由于三个周转轮系不是完全独立的,因此任取两个周转轮系求解,其结果是相同的。
(2)分别列出传动比方程式。
①定轴轮系1'-6-3'的传动比为

(传动比的正负用画箭头的方法确定)
图示定轴轮系部分是对称的,轮1'和轮3'的轴线在一直线上,且同时与轮6啮合,故其大小应相等,即z
1'=z
3',故
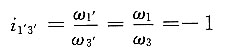
即 ω
1=-ω
3 ②差动轮系1-2-5-4的转化机构的传动比为
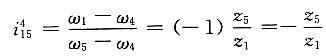
因轮1和轮5轴线重合,因此r
1=r
5+2r
2,而题设各轮模数相同,即
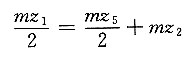
所以 z
1-z
5+2z
2=25+2×25=75
故
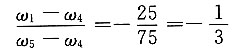
③差动轮系1-2-2'-3-4的转化机构的传动比为
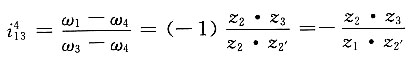
同理,因轮5和轮3的轴线在一直线上,且各轮模数相同,故
r
5+r
2=r
2'+r
3 所以 z
3-z
5+z
2-z
2'=25+25-20=30
故
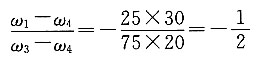
教材在推导转化机构的传动比方程式时,是假定ω
1、ω
3和ω
4的转向相同,故式中ω
1、ω
3和ω
4均为正号。但在本题所示的轮系中,当轮6的转向一定后,轮1'和轮3'的转向恒相反,即轮1和轮3的转向恒相反。因此上式中ω
1和ω
3的转向是不同的,故一个取正号,另一个须取负号,故上式应写成
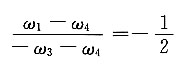
而|ω
1|=|ω
3|,故得
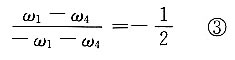
(3)联立求解i
54。
由式③得
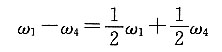
所以 ω
1=3ω
4 ④
由式②得
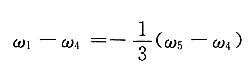
故
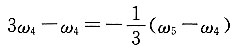
即 5ω
4=-ω
5 所以
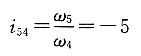
由于5、4同属周转轮系中的组成部分,且轴线重合,故i
54的符号有意义,表示齿轮5与行星架4转向相反。
12. 在如图所示的轮系中,轴A按图示方向以1250r/min的转速回转,而轴B按图示方向以600r/min的转速回转。试确定轴C的转速大小和方向。
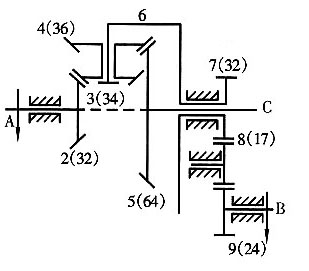
解题要点: 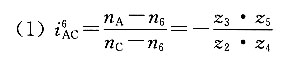
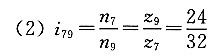
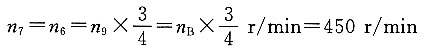
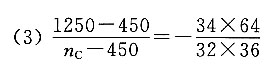
7200=-17n
C+7650
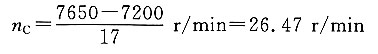
转向与n
A一致。
13. 在如图所示的轮系中,B、C和D、E做成一体,并分别空套在行星架上。齿轮A的转速为50r/min,行星架的转速为100r/min,它们的转向如图所示。试问此时齿轮F的转速和转向如何。
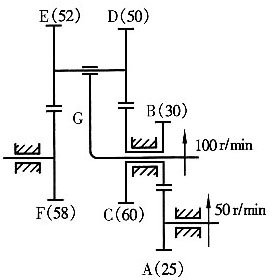
解题要点: 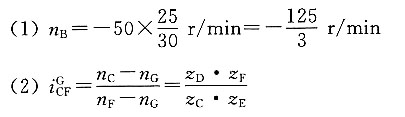
因 n
C=n
B 所以
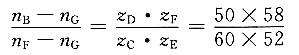
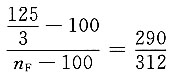
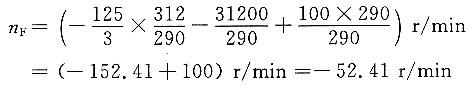
转向与n
A相反。
14. 已知2K-H行星轮系如图所示,其i
1H=9±5%,求各轮的齿数。
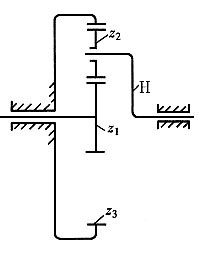
解题要点: (1)据配齿公式。
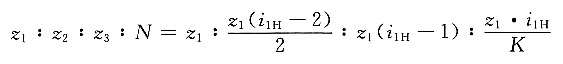
得
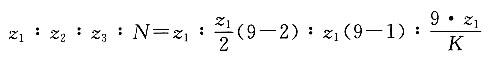
因为z
1>z
min,所以取z
1=18,故
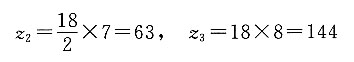
(2)求N。
设K=3,则
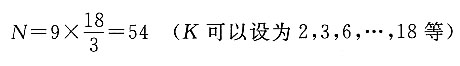
(3)验算传动比误差。
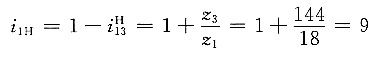
满足要求。
(4)校验邻接条件。
因为
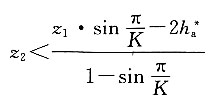
即
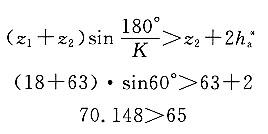
满足要求。
15. 某装配自动线上有一工作台转位机构,工作台要求有六个工位,每个工位在工作台静止时间t
j=10s内完成装配工序。当采用单销外槽轮机构时,试求:
(1)该槽轮机构的运动系数k;
(2)装圆柱销的主动构件(拨盘)的转速ω;
(3)槽轮的转位时间t
d。
解题要点:
(1)明确槽轮机构运动系数的定义及计算方法;
(2)了解槽轮机构的运动过程。
解:因为工作台要求有六个工位,所以槽轮的槽数为6,即z=6。
(1)计算槽轮机构的运动系数k。
设一个运动循环的时间为t,由槽轮机构运动系数的计算公式得
k=td/t=(t-tj)/t=1/2-1/z=1/2-1/6=1/3
(2)计算主动构件的转速ω。
由上式得 tj=t(1-1/2+1/z)=(2π/ω)(1/2+1/z)
则 ω=(2π/tj)(1/2+1/z)=(2π/10)(1/2+1/6)=0.419rad/s
(3)计算槽轮转位时间。
td=t-tj=2π/ω-tj=2π/0.419-10=5s
16. 如图所示为一磨床的进刀机构。棘轮4与行星架H固联,齿轮3与丝杆固联。已知行星轮系中各轮齿数z
1=22,z'
2=18,z
2=z
3=20,进刀丝杠的导程l=5mm。如果要求实现最小进刀量s=0.001mm,试求棘轮的最少齿数z
min。
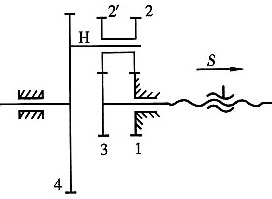
解题要点: (1)明确棘轮的最小转角为一个齿距角;
(2)由齿轮3的最小转角求出棘轮4的最小转角,从而确定棘轮的最少齿数z
min。
解:(1)求实现最小进刀量s=0.001mm时,丝杆相应的最小转角φ
3min。
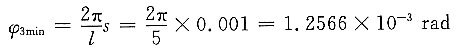
(2)求行星轮系1-2(2')-3-H的传动比i
H3及行星架H的最小转角φ
Hmin。
由
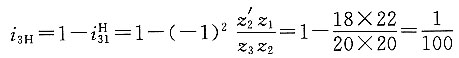
得i
H3=100,齿轮3与行星架转向相同。
故 φ
Hmin=i
H3φ
3min=100×1.2566×10
-3=0.12566rad
(3)求棘轮的最少齿数z
min。
由 z≥2π/φ
Hmin=2π/0.12566=50
故取棘轮的最少齿数 z
min=50
17. 在单万向铰链机构中,主动轴1以n
1=1000r/min匀速回转,从动轴3作变速运动,其最低转速为n
3min=766r/min。试求:
(1)主动轴与从动轴的夹角α,从动轴3的最高转速n
3max;
(2)在轴1运动一周的过程中,φ
1角为何值时两轴转速相等;
(3)从动轴的速度波动不均匀系数δ。
解题要点: 明确单万向铰链机构的角速比关系。
解:(1)因为
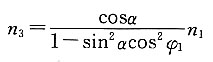
当φ
1=0°,即轴1的叉平面位于1、3两轴所在平面内时,n
3最大,有
n
3max=n
1/cosα
当φ
1=90°,即轴1的叉平面位于1、3两轴所在平面的垂直面内时,n
3最小,有
n
3min=n
1cosα
所以,有 α=arccos(n
3min/n
1)=arccos(766/1000)=40°
n
3max=n
1/cosα=1000/cos40°=1305.4r/min
(2)当n
1=n
3时,即
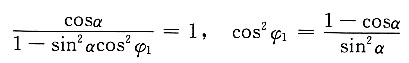
或
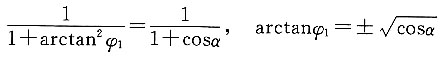
故
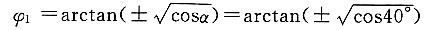
在φ
1=42.9414°,137.0586°,222.9414°,317.0586°时,两轴转速相等。
(3)求从动轴速度的波动不均匀系数。
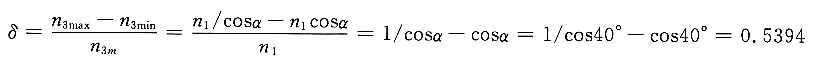
18. 如图所示的差动螺旋机构中,螺杆3与机架刚性连接,其螺纹是右旋的,导程l
A=4mm,螺母2相对机架只能移动,内外均有螺纹的螺杆1沿箭头方向转5圈时要求螺母2向左移动5mm。试求1、2螺旋副的导程l
B及其旋向。
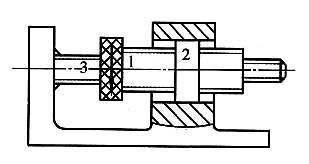
解题要点: (1)规定位移s向右为正,反之为负。
(2)导程的正负由转动方向和螺旋方向而定。若是右螺纹,则用右手按转动方向看大拇指的指向,大拇指指向为右,则为正;反之为负。若是左螺纹,则用左手按转动方向决定大拇指指向,然后定出正负。
解:因为螺母2相对机架3的位移量为
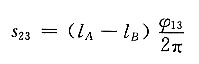
因为φ
13=5×2πrad,l
A=4mm(右旋,指向向右),s
23=-5mm(向左移动),代入上式有
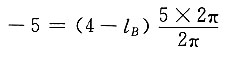
所以得 l
B=5mm
因l
B大于零,故由螺杆的转向可知,1、2螺旋副为右旋。
19. 有一双万向铰链机构,其主动端的轴间夹角等于从动端的轴间角(α
12=α
23),但主动轴1、中间轴2和从动轴3三轴轴线不在同一平面上,且中间轴两端叉面也不在同一平面上,其中主动端的叉面在主动轴和中间轴两轴轴线所在的平面上时,从动端的叉面正好在中间轴和从动轴两轴轴线所在的平面上。问此双万向铰链机构其主、从动轴间能否保持恒速比(i
31≡1)的传动。
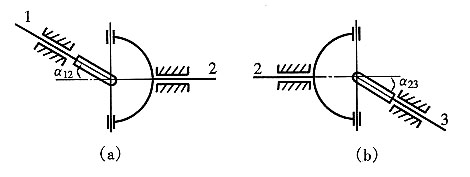
解题要点:
(1)注意了解双万向铰链机构主、从动轴要作恒速比传动应满足的三个条件,分析本例的特殊情况。
(2)对问题要进行深入的分析,不要简单地套用结论。
解:从表面上看,此问题并不满足双万向铰链机构主、从动轴要恒速比传动的三个条件,似乎不能作恒速比传动。但稍作进一步的分析就不难发现,当中间轴主动端的叉面位于主动轴和中间轴两轴轴线所在的平面上时,其情况相当于题5图(a)所示,此时有
ω2=ω1cosα12
由于此时中间轴在从动端的叉面也正好位于中间轴和从动轴两轴轴线所在的平面上,其情况相当于题图(b)所示,故有
ω3=ω2/cosα23
将上述两式联立求解,不难得到ω3=ω1,故知其主、从动轴能保持恒速比传动。
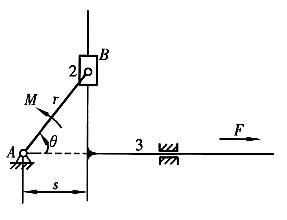
20. 在如图所示机构中,滑块3的质量为m
3,曲柄AB长为r,滑块3的速度v
3=ω
1rsinθ,ω
1为曲柄的角速度。当θ=0°~180°时,阻力F=常数;当θ=180°~360°时,阻力F=0。驱动力矩M为常数。曲柄AB绕A轴的转动惯量为J
A1,不计构件2的质量及各运动副中的摩擦。设在θ=0°时,曲柄的角速度为ω
0。试求:
(1)取曲柄为等效构件时的等效驱动力矩M
d和等效阻力矩M
r;
(2)等效转动惯量J;
(3)在稳定运转阶段,作用在曲柄上的驱动力矩M;
(4)写出机构的运动方程式。
解题要点: (1)驱动力矩M作用在等效构件上,且其他构件上无驱动力矩,故有
M
d=M
阻力F的等效阻力矩:
M
r=Fv
3/ω
1=Frsinθ(0°≤θ≤180°)
M
r=0(180°≤θ≤360°)
(2)等效转动惯量为
J=J
A1+m
3r
2sin
2θ
(3)计算稳定运转阶段,作用在曲柄上的驱动力矩M。
由M·2π=F·2r,可得

(4)机构的运动方程式:
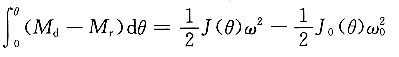

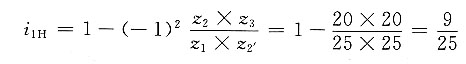
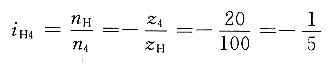
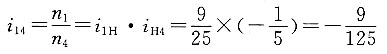

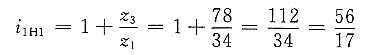
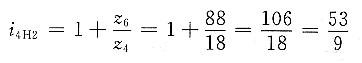
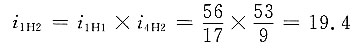

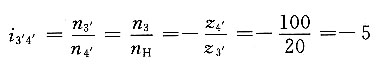
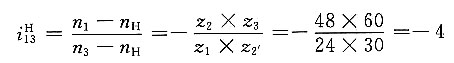
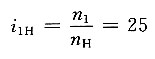

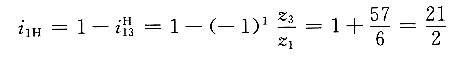
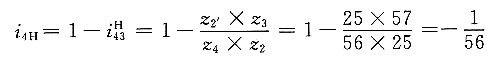
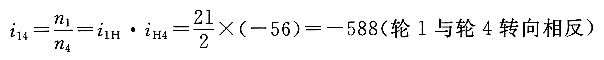

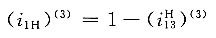
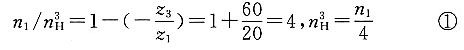
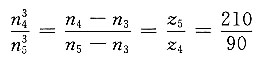
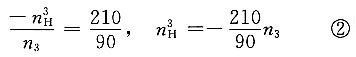

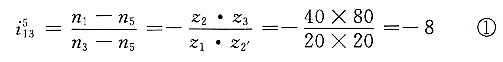
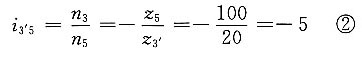
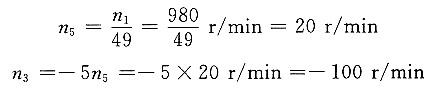


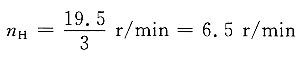 箱体的转向与n1的转向相同。
箱体的转向与n1的转向相同。


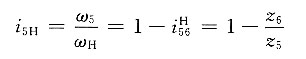
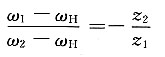
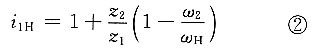
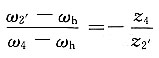
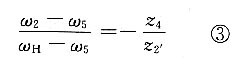
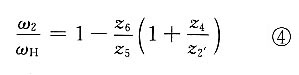
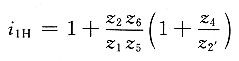

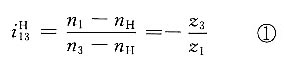
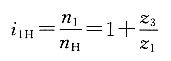
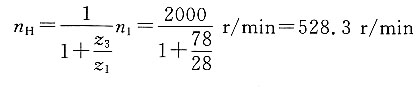
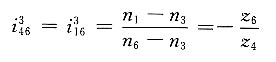
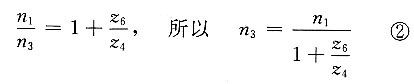
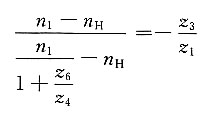
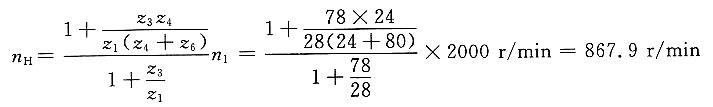

 (传动比的正负用画箭头的方法确定)
(传动比的正负用画箭头的方法确定)