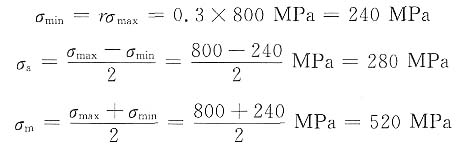计算题1. 在转塔车床上六角刀架转位用的槽轮机构中,已知槽数z=6,槽轮静止时间t
s=5/6s,运动时间t
m=2t
s,求槽轮机构的运动特性系数τ及所需的圆销数K。
解:根据题意可得,主动件转一周所需的时间:

槽轮特性系数:

又

即

则该槽轮机构所需的圆销数K=2。
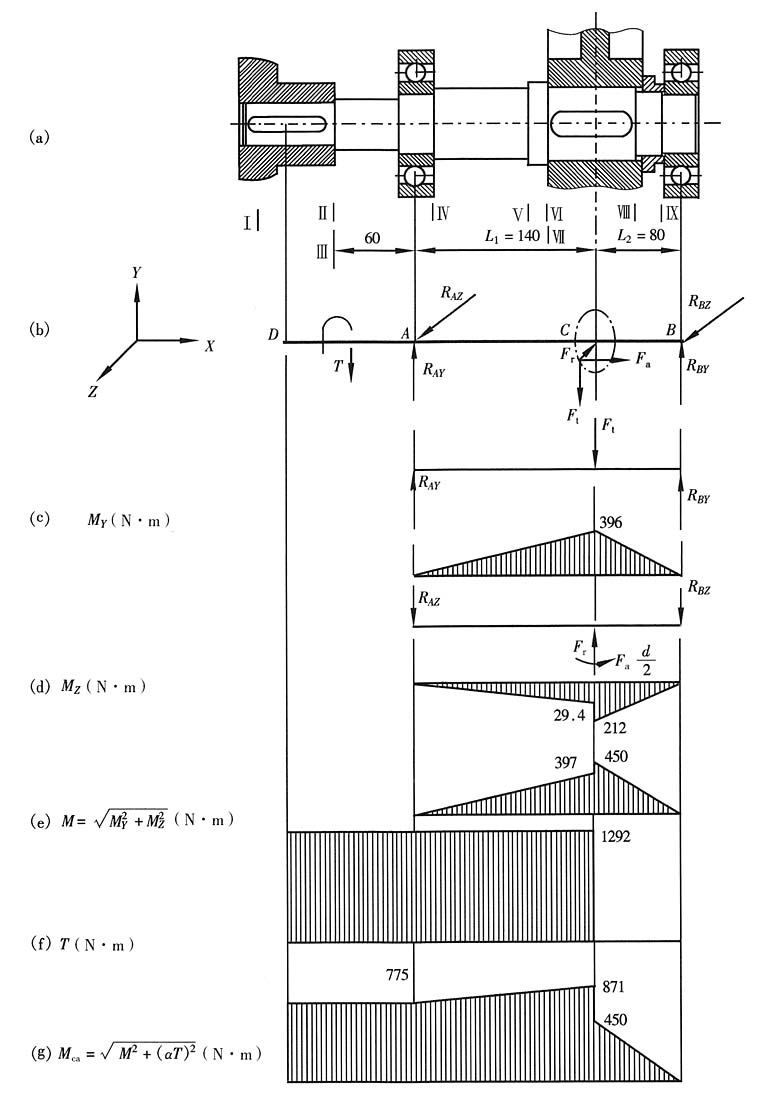
3. 计算支承反力;
求支承反力。
①求垂直面支承反力。
由∑M
B=0,得
-R
AY(L
1+L
2)+F
tL
2=0
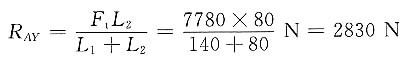
由∑Y=0,得
R
BY=F
t-R
AY=(7780-2830)N=4950N
②求水平面支承反力。
由∑M
B=0,得
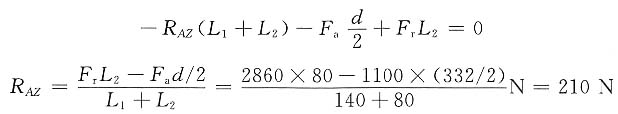
由∑z=0,得
R
BZ=F
r-R
AZ=(2860-210)N=2650N
4. 画出轴的弯矩图、合成弯矩图及转矩图;
画出轴的弯矩图、合成弯矩图及转矩图。
①垂直面弯矩M
Y图如上图(c)所示。
C点:
M
CY=R
AYL
1=2830×140N·mm=3.96×10
5N·mm
②水平面弯矩M
Z图如上图(d)所示。
C点左边:
M
CZ=R
AZL
1=210×140N·mm=2.94×10
4N·mm
C点右边:
M'
CZ=R
BZL
2=2650×80N·mm=2.12×10
5N·mm
③合成弯矩M图上图(e)所示。
C点左边:
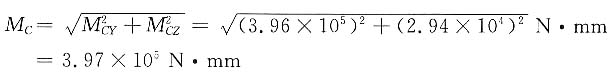
C点右边:
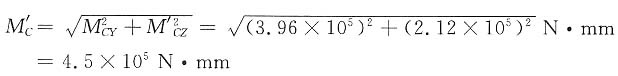
④作转矩图如上图(f)所示。
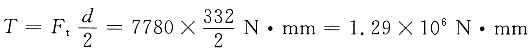
⑤作计算弯矩图如上图(g)所示。
该轴单向工作,转矩产生的剪切应力按脉动循环应力考虑,取α=0.6。
C点左边:
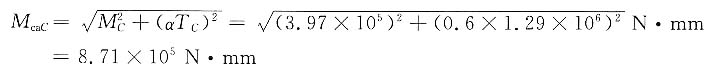
C点右边:
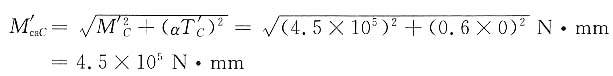
D点:
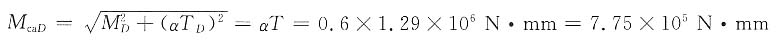
5. 指出危险剖面的位置。
指出危险剖面的位置。
上图(a)中,Ⅰ~Ⅸ均为有应力集中的剖面,均有可能是危险剖面。其中Ⅰ~Ⅳ剖面的计算弯矩相同。Ⅱ剖面与Ⅲ剖面相比较,只是应力集中影响不同,可以取应力集中系数较大者进行验算即可。同理,Ⅵ、Ⅶ剖面承载情况也比较接近,可取应力集中系数较大者进行验算。
6. 有一薄转盘质量为m,经静平衡试验测定其质心偏距为r,方向如图所示垂直向下。由于该回转面不允许安装平衡质量,只能在平面Ⅰ、Ⅱ上校正。已知m=10kg,r=5mm,a=20mm,b=40mm。求在Ⅰ、Ⅱ平面上应加的质径积的大小和方向。
解:确定质径积的大小:mr=10×5=50kg·mm=0.05kg·m。
将该不平衡质径积在平面Ⅰ和平面Ⅱ内分解,则:
在平面Ⅰ中,有

故应加质径积为0.1kg·m,方向垂直向上。
在平面Ⅱ中,有

故应加质径积为-0.05kg·m,方向垂直向下。
7. 在如图所示两级斜齿圆柱齿轮减速器中。已知中间轴Ⅱ传递的功率P=40kW,转速n
2=200r/min,齿轮2的分度圆直径d
2=688mm,螺旋角β
2=12°50’,齿轮3的分度圆直径d
3=170mm,螺旋角β
3=10°29',轴的材料用45钢调质,试按弯扭合成强度计算方法求轴Ⅱ的直径。
解:轴的材料选用45钢调质处理,查表得其许用弯曲应力[σ
-1b]=60MPa。
由题图可知,轴Ⅱ传递的扭矩

(1)做出轴Ⅱ的受力简图,如图(a)所示。
齿轮1、2啮合点处的作用力

F
a2=F
t2tanβ
2=5552×tan12°50'=1264N
齿轮3、4啮合点处的作用力

F
a3=F
t3tanβ
3=22471×tan10°29'=4157N
(2)求垂直面的支反力
由题图可知

在径向力作用平面内

F
2V=F
r2-F
r3-F
1V=2073-8318+2611=-3634N
在圆周力作用平面内

F
2H=-F
t2-F
t3-F
1H=-5552-22471+11303=-16720N
(3)计算弯矩并绘制弯矩图
①径向力作用平面内
M
B左V=F
1VL
1=-2611×100=-261100N·mm

绘制径向力作用平面内弯矩图如图(b)所示。
②圆周力作用平面内
M
BH=F
1HL
1=-11303×100=-1130300N·mm
M
CH=F
1H(L
1+L
2)+F
t2L
2=-11303×(100+225)+5552×225=-2424275N·mm
绘制圆周力作用平面内弯矩图如图(c)所示。
③合成弯矩
由径向力作用平面内弯矩图和圆周力作用平面内弯矩图可知,C点左侧(即齿轮3左侧面)弯矩最大,为

(4)绘制扭矩图,如图(d)所示,T=1910000N·mm。
(5)轴的扭转切应力为脉动循环应力,取折合系数α=0.6,则当量弯矩值为

(6)根据弯扭合成强度条件可得

由于该轴上有键槽,因此将轴径增大3%~5%,取d=1.04×77.77=80.8808mm,取d=82mm。
8. 起重卷筒与大齿轮用8个普通螺栓连接在一起,如下图所示。已知卷筒直径D=400mm,螺栓分布圆直径D
0=500mm,接合面间摩擦系数f=0.12,可靠性系数K
f=1.2,起重钢索拉力Q=50000N,螺栓材料的许用拉伸应力[σ]=100MPa。试设计该螺栓组的螺栓直径。
解题要点: 1.计算旋转力矩T
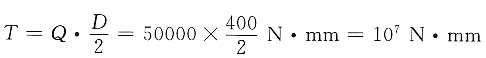
2.计算螺栓所需要的预紧力F'
由

得
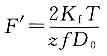
将已知数值代入上式,可得
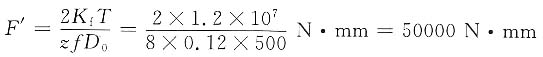
3.确定螺栓直径
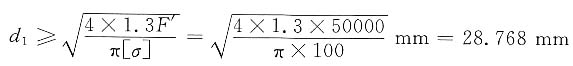
取M36(d
1=31.670mm>28.768mm)。
讨论:(1)此题也可改为校核计算题,已知螺栓直径,校核其强度。其解题步骤仍然是需先求F',然后验算
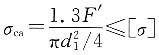
。
(2)此题也可改为计算起重钢索拉力Q。已知螺栓直径,计算该螺栓所能承受的预紧力F',然后按接合面间摩擦力矩与作用于螺栓组连接上的旋转力矩相平衡的条件,求出拉力Q,即由
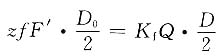
得
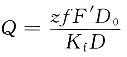
[解析] 本题是典型的仅受旋转力矩作用的螺栓组连接。由于本题是采用普通螺栓连接,是靠接合面间的摩擦力矩来平衡外载荷——旋转力矩,因此本题的关键是计算出螺栓所需要的预紧力F'。而本题中的螺栓仅受预紧力F'作用,故可按预紧力F'来确定螺栓的直径。
9. 斜齿圆柱齿轮的齿数z与其当量齿数z
v有什么关系?在下列几种情况下应分别采用哪一种齿数:
(1)计算斜齿圆柱齿轮传动的角速比;
(2)用成形法切制斜齿轮时选盘形铣刀;
(3)计算斜齿轮的分度圆直径;
(4)弯曲强度计算时查取齿形系数。
斜齿圆柱齿轮的齿数z和当量齿数Z
v的关系:

(1)齿数z;(2)当量齿数z
v;(3)齿数z;(4)当量齿数z
v。
10. 一单头蜗杆传动,已知蜗轮的齿数z
2=40,蜗杆的直径系数q=10,蜗轮分度圆直径d
2=200mm。试求:
(1)模数m、轴向周节p
a1,蜗杆分度圆直径d
1,中心距a及传动比i
12 (2)若当量摩擦系数f
v=0.08,求蜗杆、蜗轮分别为主动件时的效率η及η';
(3)若改用双头蜗杆,其η、η'又为多少?
(4)从效率η与η'的计算中可得出什么结论?
解题要点: (1)模数 m=d
2/z
2=200/40mm=5mm
(2)周节 p
a1=πm=π×5mm=15.708mm
(3)蜗杆直径 d
1=mq=5×10mm=50mm
(4)传动比 i
12=z
2/z
1=40/1=40
(5)中心距 a=0.5m(q+z
2)=0.5×5×(10+40)mm=125mm
(6)计算效率如下。
①单头蜗杆传动

γ=arctan0.1=5°42'38"
ρ
v=arctanf
v=arctan0.08=4°34'26"
蜗杆为主动时
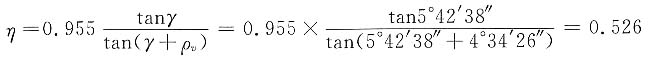
蜗轮为主动时
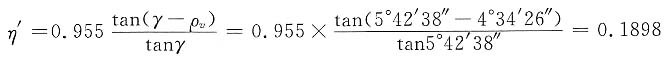
②对双头蜗杆传动
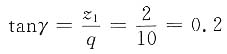
γ=arctan0.2=11°18'35"
蜗杆为主动时
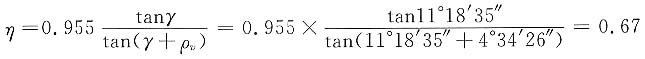
蜗轮为主动时
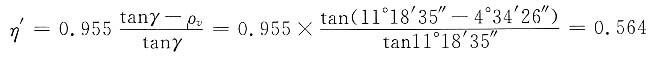
(7)通过对不同头数的蜗杆主动或是蜗轮主动时的效率计算,可知:
①双头蜗杆的效率比单头蜗杆高;
②相同条件下,蜗杆主动的效率比蜗轮主动时的效率高。
11. 在图所示机构中,已知z
1=17,z
2=20,z
3=85,z
4=18,z
5=24,z
6=21,z
7=63,求:
(1)当n
1=10001r/min、n
4=10000r/min时,n
p=?
(2)当n
1=n
4时,n
p=?
(3)当n
1=10000r/min、n
4=10001r/min时,n
p=?
解:这是一个混合轮系,其中:
齿轮1、2、3构成定轴轮系,有

(1)
齿轮4、5、6、7和由齿轮3引出的杆件H构成周转轮系,有

(2)
又n
H=n
3,n
p=n
7,联立式(1)和(2)可得

(1)当n
1=10001r/min、n
4=10000r/min时,可得

p和转向和齿轮1的转向相同。
(2)当n
1=n
4时,n
p=0。
(3)当n
1=10000r/min、n
4=10001r/min时,可得

p的转向和齿轮1的转向相反。
12. 基孔制优先配合为


试以公称尺寸为50mm绘制其公差带图。
解:各个公差带图如图所示,基本尺寸与公差带尺寸均为mm。
(1)

其公差带如图(a)所示。
(2)

其公差带如图(b)所示。
(3)

其公差带如图(c)所示。
(4)

其公差带如图(d)所示。
(5)

其公差带如图(e)所示。
(6)

其公差带如图(f)所示。
其余略。
13. 某轴只受稳定交变应力作用,工作应力σ
max=240MPa,σ
min=-40MPa。材料的力学性能σ
-1=450MPa,σ
s=800MPa,σ
0=700MPa,轴上危险截面的k
σ=1.30,ε
σ=0.78,β=1。
(1)绘制材料的简化应力图;
(2)用作图法求极限应力σ
r及安全系数(按r=c加载和无限寿命考虑);
(3)取S=1.3,试用计算法验证作图法求出的σ
ra、σ
rm及S
ca值,并校验此轴是否安全。
解题要点: (1)绘制材料的极限应力图。
根据各点坐标A(0,450)、B(350,350)及S(800,0),按前述方法即可绘制此图(见下图)。
(2)绘制零件的极限应力图。
各点坐标为:
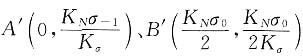
及S(σ
s,0),代入数值后为
A'(0,270),B'(350,210),S(800,0)
由点A'、B'及S,按前述方法可绘出该图。
(3)在图上标出工作应力点M。
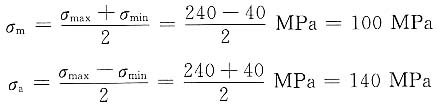
则工作应力点的坐标为M(100,140),并标于图上。
(4)由作图法求极限应力σ
ra、σ
rm及安全系数S
σ。
由图大致量得
σ
rm=170MPa, σ
ra=241MPa
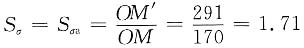
(5)用计算法验证。
由
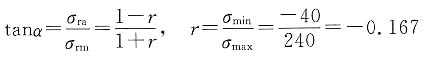
所以

疲劳强度极限线A'E'的直线方程为
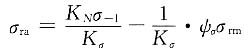
式中

所以
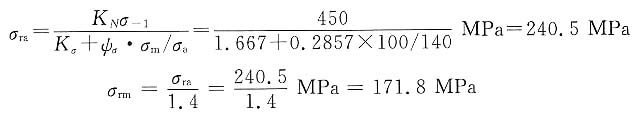
校核轴的疲劳强度
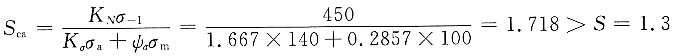
故此轴疲劳强度达到安全要求。
14. 一圆柱蜗杆减速器,蜗杆轴功率P
1=100kW,传动总效率η=0.8,三班制工作。试按所在地区工业用电价格(每千瓦小时若干元)计算五年中用于功率损耗的费用。
解:估计一年有250个工作日,用电价格为a元每千瓦时。于是5年中功率损耗的费用:P1(1-η)×250×3×8×5a=6×105a(元)。
15. 指出机构运动简图中的复合铰链、局部自由度和虚约束,计算各机构的自由度。

机械手
解:图所示机构的自由度为
F=3n-2PL-PH=3×3-2×3=3
16. 有一直齿圆柱齿轮传动,允许传递功率P,若通过热处理方法提高材料的力学性能,使大、小齿轮的许用接触应力[σ
H2]、[σ
H1]各提高30%,试问此传动在不改变工作条件及其他设计参数的情况下,抗疲劳点蚀允许传递的扭矩和允许传递的功率可提高百分之几?
解:根据标准齿轮齿面接触疲劳强度条件

可知抗疲劳点蚀允许的最大扭矩满足:

因此,当许用接触应力提高30%时,有

则T提高69%。
又由

可知,功率P也提高了69%。
17. 在下图中,已知小带轮为主动轮,试证明带传动中紧边带速v
1大于松边带速v
2。
证明:v
1>v
2。在题图中,a点为参考点,是带与小带轮紧边的切点(即带绕进小带轮的点)。在Δt时间内,小带轮上的a点转到b点,小带轮的圆周速度

。
带传动工作时,带受到拉力后要产生弹性变形,由于紧边和松边的拉力不同,因此相应的弹性变形也不同,带在带轮上产生弹性滑动,故带在同一Δt时间内只由a点转到e点,而带的圆周速度
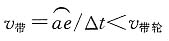
带进入小带轮一边为紧边 v
带轮=v
1 带离开小带轮一边为松边 v
带=v
2 所以 v
1>v
2
18. 在图所示钟表传动示意图中,E为擒纵轮,N为发条盘,S、M、H分别为秒针、分针、时针。设z
1=72,z
2=12,z
3=64,z
4=8,z
5=60,z
6=8,z
7=60,z
8=6,z
9=8,z
10=24,z
11=6,z
12=24。求秒针与分针的传动比i
SM和分针与时针的传动比i
MH。
解:秒针到分针的传递路线为:6→5→4→3,齿轮3上带着分针,齿轮6上带着秒针,因此

分针到时针的传递路线为:9→10→11→12,齿轮9上带着分针,齿轮12上带着时针,因此

19. 有一变位蜗杆传动,已知模数m=6mm,传动比i=20,直径系数q=9,蜗杆头数z
1=2,中心距(变位后)a'=150mm。
试求其变位系数χ及该传动的几何尺寸,并分析哪些尺寸不同于未变位蜗杆传动。
解题要点: (1)求变位系数χ。
z
2=iz
1=20×2=40
a=0.5m(q+z
2)=0.5×6×(9+40)mm=147mm
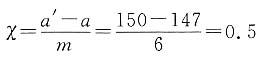
(2)求变位后的几何尺寸。
变位后蜗杆的几何尺寸保持不变。但在啮合中,蜗杆节圆不再与分度圆重合。该变位蜗杆传动的蜗杆节圆直径为
d'
1=d
1+2χm=mq+2χm=(6×9+2×0.5×6)mm=60mm变位后,蜗轮顶圆直径d
a2齿根圆直径d
f2分别为
d
a2=(z
2+2h
a*+2χ)m=(40+2×1+2×0.5)×6mm=258mm
d
f2=(z
2-2h
a*+2χ-2c
1*)m=(40-2+2×0.5-2×0.2)×6mm=231.6mm变位后,蜗轮分度圆直径d
2、节圆直径d'
2及宽度b
2仍保持不变。
20. 已知某钢材的力学性能为σ
-1=500MPa,σ
s=1000MPa,σ
0=800MPa。
(1)试按比例绘制该材料的简化疲劳极限应力图;
(2)由该材料制成的零件,承受非对称循环应力,其应力循环特性r=0.3,工作应力σ
max=800MPa,零件的有效应力集中系数k
σ=1.49,零件的尺寸系数ε
σ=0.83,表面状态系数β=1,按简单加载情况在下图中标出工作应力点及对应的极限应力点;
(3)判断该零件的强度是否满足要求。
解题要点: (1)绘制材料的简化疲劳极限应力图。
因材料为塑性材料,故极限应力图用σ
m-σ
a极限应力图表示。确定极限应力图折线ABS上的各点坐标:A(0,σ
-1)、S(σ
s,0)及B(σ
0/2,σ
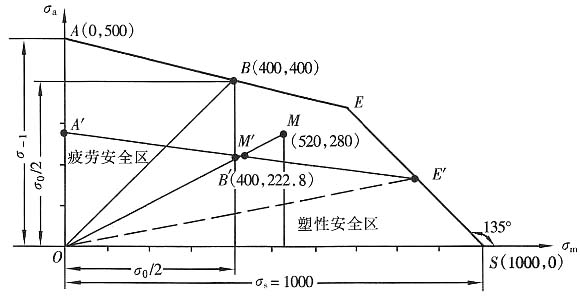
0/2),代入数值后为:A(0,500)、B(400,400)及S(1000,0),连接直线AB与自点S作与横坐标轴成135°的斜线交于点E,则ABES折线为极限应力图(见下图)。
(2)绘制零件的许用极限应力图。
由题意寿命系数K
N=1.0,对材料的极限应力曲线进行修正。
点A对应的点A'的坐标为
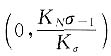
,式中
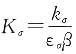
,代入数据后为A'(0,278.5)。
点B对应的点B'的坐标为
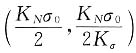
,代入数据后为B'(400,222.8)。
对点S不必进行修正。连接A'B'线与原SE线交于点E',则零件的许用极限应力折线图为A'B'E'S。
(3)确定工作应力点M的坐标。
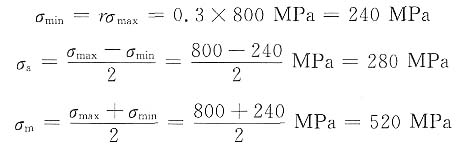
所以工作应力点的坐标为M(520,280)。
(4)按简单加载情况,过原点O连射线OM交A'B'E'于点M',该点即为极限应力点。
(5)点M落在疲劳安全区OA'E'以外,该零件发生疲劳破坏。
21. 已知一对直齿锥齿轮的传动比i=2.5,压力角α=20°,齿宽中点分度圆的圆周力F
t1=5600N,斜齿圆柱齿轮分度圆螺旋角β=11°36',分度圆的圆周力F
t2=9500N。试求:轴Ⅱ上的轴向力的大小和方向。螺旋角β的方向如下图(a)所示。
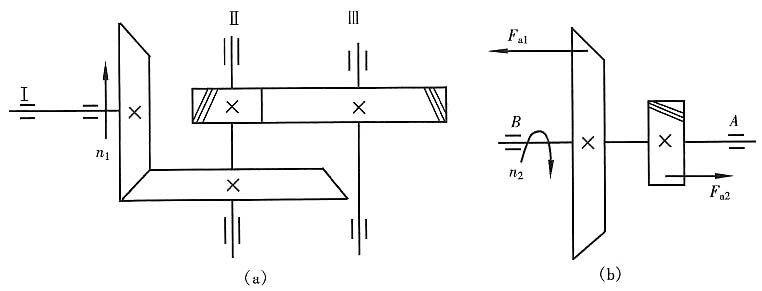
(注:直齿圆柱齿轮与斜齿圆柱齿轮轴向力计算公式分别为:F
a1=F
t1tanαsinδ
1;F
a2=F
t2tanβ)
解题要点:
设锥齿轮的轴向力为Fa1,圆柱齿轮的轴向力为Fa2,则
Fa1=Ft1tanαsinδ1
而tanδ1=1/u=1/2.5=0.4,有δ1=21°48'5",故
Fa1=5600×tan20°sin21°48'5"N=757N
Fa2=Ft2tanβ=9500×tan11°36'N=1950N
则轴Ⅱ上的轴向力为
Fa=Fa2-Fa1=(1950-757)N=1193N
Fa的方向指向点A(见题图(b))。
22. 试设计某轻纺机械一转轴上的非液体摩擦向心滑动轴承。已知轴颈直径为55mm,轴瓦宽度为44mm,轴颈的径向载荷为24200N,轴的转速为300r/min。
解:该轴承的压强p为

其pv值为

由p值和pv值对照表可知,选用铸铝青铜ZCuA110Fe3作为轴瓦材料即可满足要求,其许用值[p]=15MPa,[pv]=12MPa·m/s。
轴承选用润滑脂润滑,用油杯加脂。
23. 某工程机械传动中轴承配置形式如图所示。已知轴承型号为30311。判别系数e=0.35,内部轴向力为F
s=F
r/2Y,其中Y=1.7。当F
a/F
r≤e时,X=1,Y=0;当F
a/F
r>e时,X=0.4,Y=1.7。两轴承的径向载荷F
r1=4000N,F
r2=5000N,外加轴向载荷F
A=2000N,方向见下图,试画出内部轴向力F
s1、F
s2的方向,并计算轴承的当量动载荷P
1、P
2。
解:由题意可知,两轴承的派生轴向力分别为

轴向力F
s1,F
s2的方向如图所示。
因为
F
s2+F
A=3470.59N>F
s1=1176.47N
则轴承1为压紧端,轴承2为放松端。两轴承的轴向载荷分别为
F
a1=F
A+F
s2=3470.59N
F
a2=F
s2=1470.59N
由

可得X
1=0.4,Y
1=1.7;X
2=1,Y
2=0。
因此两轴承的当量动载荷分别为
P
1=X
1F
r1+Y
1F
a1=0.4×4000+1.7×3470.59=7500.003N
P
2=X
2F
r2+Y
2F
a2=1×5000+0=5000N


 即
即 则该槽轮机构所需的圆销数K=2。
则该槽轮机构所需的圆销数K=2。
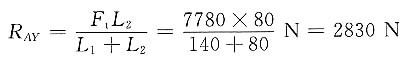
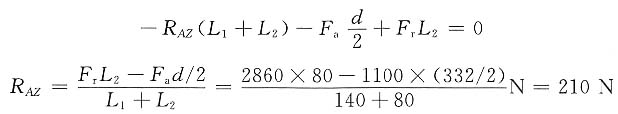
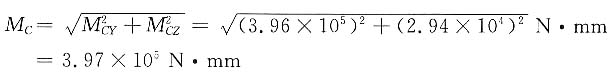
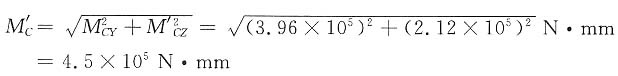
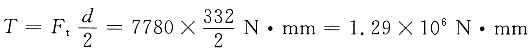
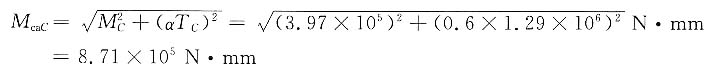
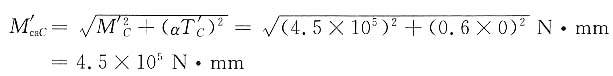
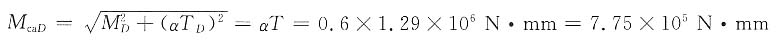
















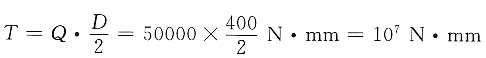

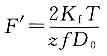
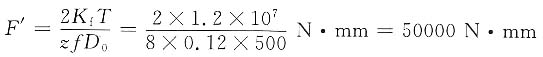
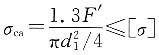 。
。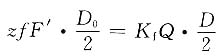
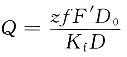


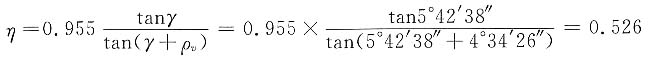
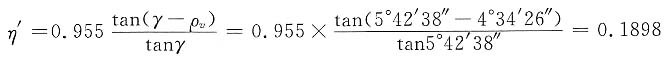
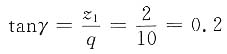
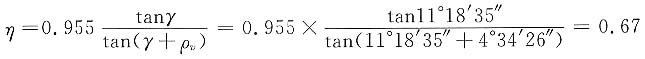
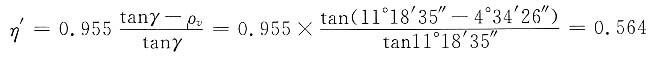

 (1)
(1) (2)
(2)



 试以公称尺寸为50mm绘制其公差带图。
试以公称尺寸为50mm绘制其公差带图。 其公差带如图(a)所示。
其公差带如图(a)所示。 其公差带如图(b)所示。
其公差带如图(b)所示。

 其公差带如图(c)所示。
其公差带如图(c)所示。 其公差带如图(d)所示。
其公差带如图(d)所示。 其公差带如图(e)所示。
其公差带如图(e)所示。 其公差带如图(f)所示。
其公差带如图(f)所示。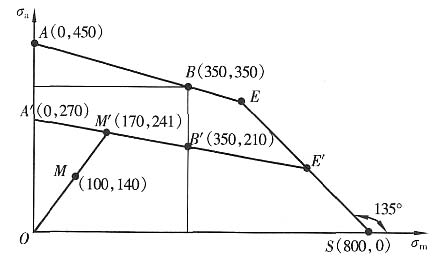
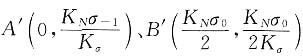 及S(σs,0),代入数值后为
及S(σs,0),代入数值后为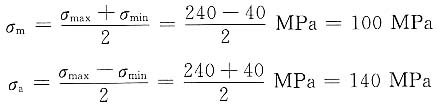
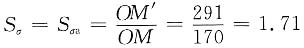
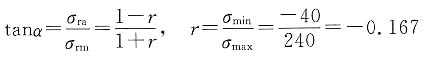

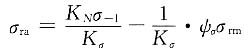

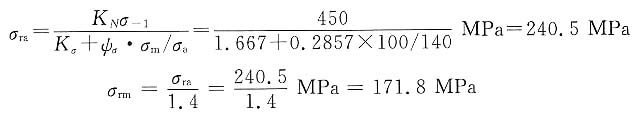
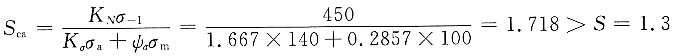

 可知抗疲劳点蚀允许的最大扭矩满足:
可知抗疲劳点蚀允许的最大扭矩满足:
 则T提高69%。
则T提高69%。 可知,功率P也提高了69%。
可知,功率P也提高了69%。
 。
。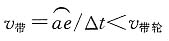



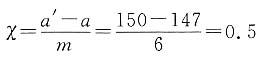
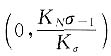 ,式中
,式中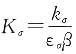 ,代入数据后为A'(0,278.5)。
,代入数据后为A'(0,278.5)。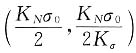 ,代入数据后为B'(400,222.8)。
,代入数据后为B'(400,222.8)。