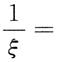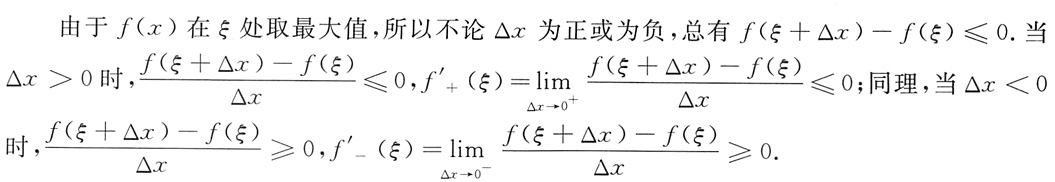一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的.)1. 若函数f(x)=log
2(x+1),且a>b>c>0,则
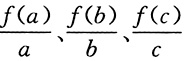
的大小关系是______
A.
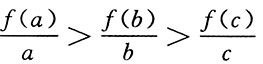
B.
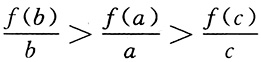
C.
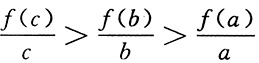
D.
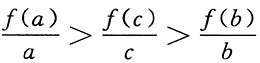
A B C D
C
[解析] 因为f(0)=0,所以
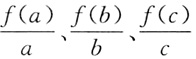
可看作函数的图象上的点与原点所确定的直线的斜率,根据函数f(x)=log
2(x+1)的图象及a>b>c>0可知
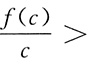
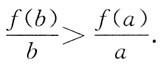
2. 在空间直角坐标系中,由参数方程
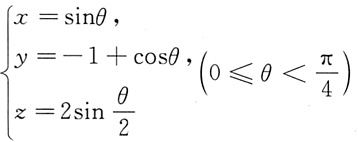
确定的曲线的一般方程是______
A.
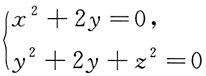
B.
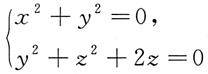
C.
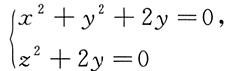
D.
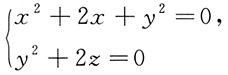
A B C D
C
[解析] 由x=sinθ,y=-1+cosθ,且sin
2θ+cos
2θ=1,得x
2+y
2+2y=0.由cosθ=

3. 设f(x),g(x)在区间[a,b]上连续,且g(x)<f(x)<m,则由曲线y=g(x),y=f(x)及直线x=a,x=b所围成的平面区域绕直线y=m旋转一周所得旋转体体积为______
A.
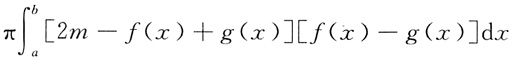
B.
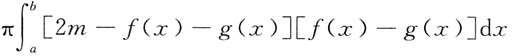
C.
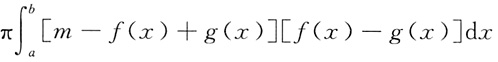
D.
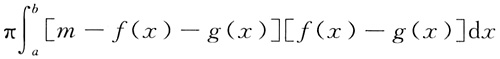
A B C D
B
[解析] 由题意得,dV={π[m-g(x)]
2-π[m-f(x)]
2}dx=π[2m-f(x)-g(x)][f(x)-g(x)]dx,则
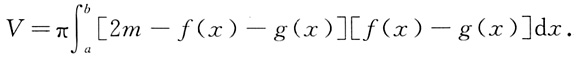
4. 设
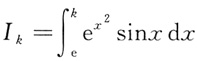
(k=1,2,3),则有______
- A.I1<I3<I2
- B.I2<I1<I3
- C.I2<I3<I1
- D.I1<I2<I3
A B C D
D
[解析] 将
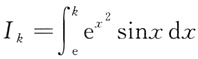
(k=1,2,3)看作以k为自变量的函数,则可知I'
k=e
k2sink>0,k∈(0,π),即可知
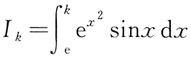
(k=1,2,3)关于k在(0,π)上为单调增函数.又由于(1,2,3)∈(0,π),则I
1<I
2<I
3.
6. 函数

的图象大致为______
A.
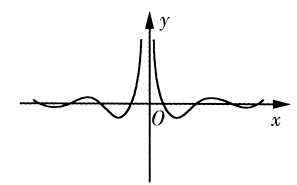
B.
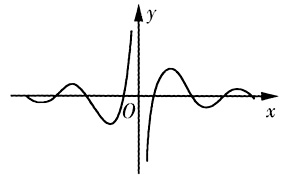
C.
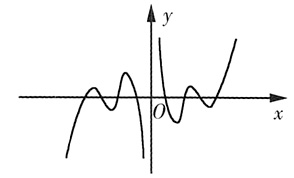
D.
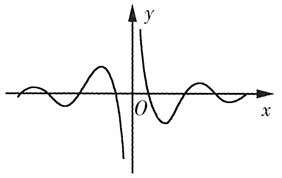
A B C D
D
[解析] 由于f(x)是奇函数,排除A.当x→+∞时,f(x)→0,排除C.当x>0且x→0时,f(x)→+∞,排除B,故选D.
二、简答题(每小题7分,共35分)袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球,以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数.2. 求二维随机变量(X,Y)的概率分布.
X,Y的可能取值均为0,1,2,且
3. 数学教学中恰当地运用提问的艺术,往往可以激起师生互动、展开提问、进行探究.提问要有明确的指向,还要有“问”的技巧.你认为应注意哪些问题才能提高课堂提问的有效性.
数学教学中恰当地运用提问的艺术,往往可以激起师生互动、展开讨论、进行探究,提高课堂提问的有效性应注意:
(1)提问要有明确的指向、明确的目的,这会大大增强提问的针对性,提高教学效率.
(2)提问需要设置情境,构造“问”的氛围,使“问”得自然,“问”到点子上,“问”出效果来.
(3)在“问”的方式上下功夫,当学生无疑可问时,可通过“设问”来引出问题;当学生思维受阻时,可通过“点问”来指点迷津;当学生对问题的认识还流于表面时,可通过“追问”引领学生将探究深入下去;当学生有疑问而有依赖倾向时,可通过“反问”来激励学生自主探究;当学生面对问题茫然时,可通过“海问”来引发学生的“点问”,反思相关的知识与方法等.
4. 利用定积分求椭圆
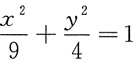
所围图形的面积.
5. 求曲面z-e
z+2xy=3在点(1,2,0)处的切平面及法线方程.
令F(x,y,z)=z-e
z+2xy-3,
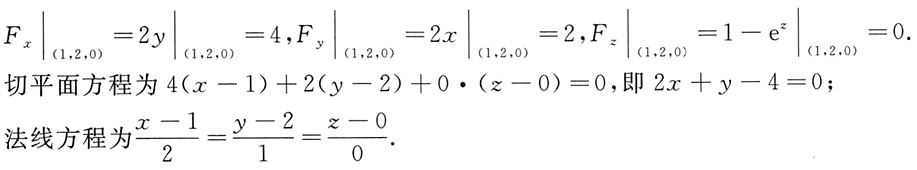
6. 应用拉格朗日中值定理证明下列不等式:
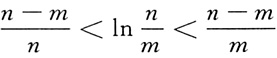
,其中0<m<n.
证明:设f(x)=lnx,
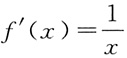
,则f(x)在[m,n]上连续,在(m,n)内可导,故函数f(x)在[m,n]上满足拉格朗日中值定理,则在(m,n)上存在一点ξ,使得
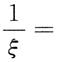

三、解答题(本大题10分)1. 罗尔定理:设函数f(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)f(a)=f(b),则在(a,b)内至少存在一点ξ,使得f'(ξ)=0.证明这个定理并说明其几何意义.
(1)证明:因为f(x)在闭区间[a,b]上连续,所以在[a,b]上一定取到最大值M和最小值m.
①若M=m,则f(x)在[a,b]上是常数,f(x)=M,x∈[a,b].从而f'(x)=0,因此,任取ξ∈(a,b)都有f'(ξ)=0.
②若M≠m,则M,m中至少有一个不等于f(a),不妨设f(a)≠M.因此,函数f(x)在(a,b)内某一点ξ处取到最大值M.我们来证f'(ξ)=0.
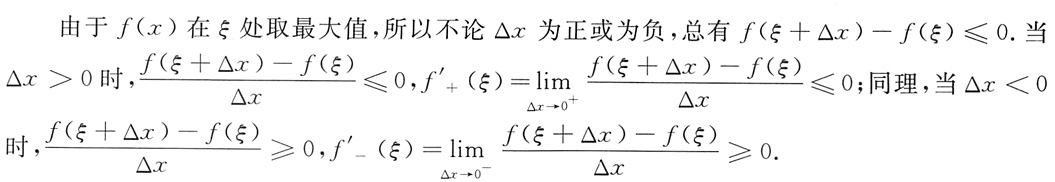
根据题意,f(x)在ξ点处可导,所以f'(ξ)=0,得证.
(2)几何意义:设y=f(x)是一条连续光滑的曲线,并且在点A、B处的纵坐标相等,即f(a)=f(b),如图,那么我们容易看出,在弧AB上至少有一点C(ξ,f(ξ)),使得曲线在C点有水平切线.
四、论述题(本大题15分)1. 请你谈谈对“课程内容的选择要贴近学生的实际,有利于学生体验与理解、思考与探索”的理解.
(1)数学课程是学生吸取数学知识和经验的主要载体之一,它精选人类在千百年中已经认识到的有关的间接知识和经验,并将其加工、改造和浓缩,以教科书的形式呈现给学生.在数学学习中,学生主要是借助原有的经验和知识,在教师的指导下,通过各种有效方式,吸取这些知识和经验,所以,课程内容的选择要适合学生思维、贴近学生实际(包括生活实际和数学实际).
(2)动手实践、自主探索和合作交流是数学学习的重要方式,它们凸显了学习过程之中的发现、研讨等探索活动,有了学习过程中的体验,知识的学习不再仅仅属于认知、理性范畴,它已扩展到情感、生理和人格等领域,从而使学习过程不仅是知识增长的过程,同时也是身心和人格健全与发展的过程.我们的学校教育也应该给学生这样的空间,所以课程内容的选择要有利于学生体验与理解、思考与探索.
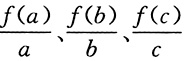 的大小关系是______
的大小关系是______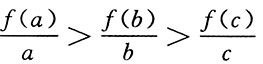
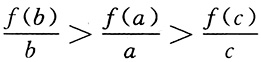
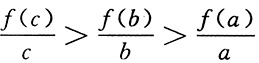
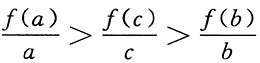
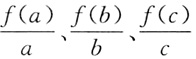 可看作函数的图象上的点与原点所确定的直线的斜率,根据函数f(x)=log2(x+1)的图象及a>b>c>0可知
可看作函数的图象上的点与原点所确定的直线的斜率,根据函数f(x)=log2(x+1)的图象及a>b>c>0可知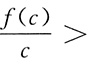
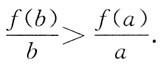
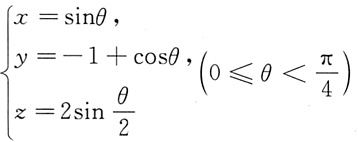 确定的曲线的一般方程是______
确定的曲线的一般方程是______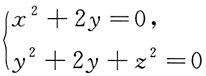
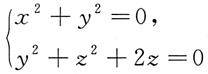
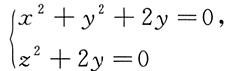
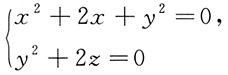

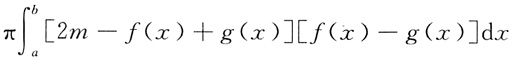
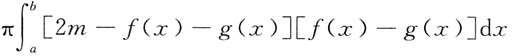
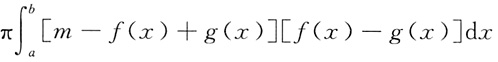
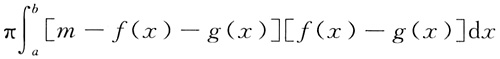
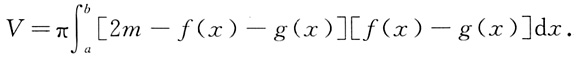
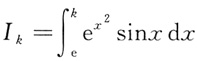 (k=1,2,3),则有______
(k=1,2,3),则有______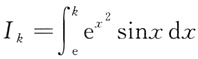 (k=1,2,3)看作以k为自变量的函数,则可知I'k=ek2sink>0,k∈(0,π),即可知
(k=1,2,3)看作以k为自变量的函数,则可知I'k=ek2sink>0,k∈(0,π),即可知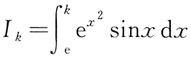 (k=1,2,3)关于k在(0,π)上为单调增函数.又由于(1,2,3)∈(0,π),则I1<I2<I3.
(k=1,2,3)关于k在(0,π)上为单调增函数.又由于(1,2,3)∈(0,π),则I1<I2<I3. 的图象大致为______
的图象大致为______



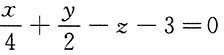 的位置关系是______
的位置关系是______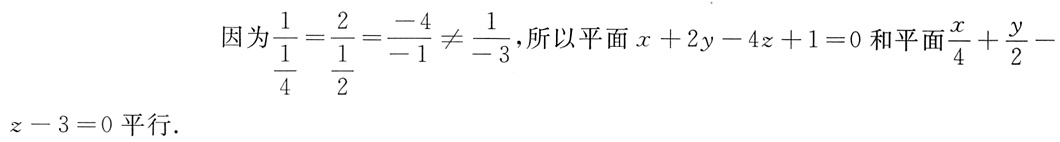
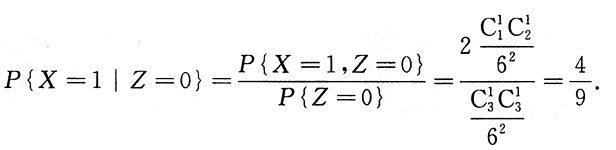

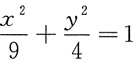 所围图形的面积.
所围图形的面积.
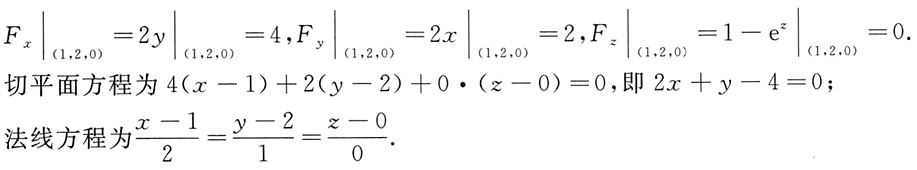
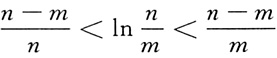 ,其中0<m<n.
,其中0<m<n.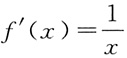 ,则f(x)在[m,n]上连续,在(m,n)内可导,故函数f(x)在[m,n]上满足拉格朗日中值定理,则在(m,n)上存在一点ξ,使得
,则f(x)在[m,n]上连续,在(m,n)内可导,故函数f(x)在[m,n]上满足拉格朗日中值定理,则在(m,n)上存在一点ξ,使得