银符考试题库B12
现在是:
试卷总分:150.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
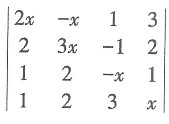 中x3的系数为______.
中x3的系数为______.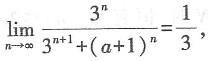 则a的取值范围是______.
则a的取值范围是______.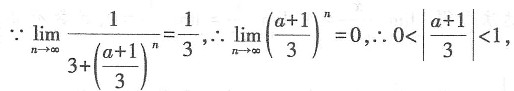
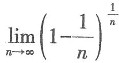 的值是______.
的值是______.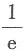
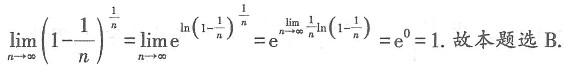
 是______.
是______.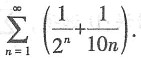 因
因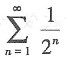 收敛,
收敛,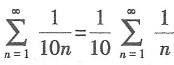 发散,则加括号后级数发散.故本题选C.
发散,则加括号后级数发散.故本题选C.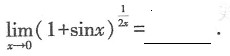
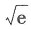
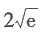
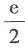
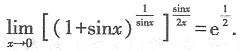
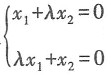 有非零解,则λ=______.
有非零解,则λ=______.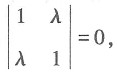 因此可得1-λ2=0.解得λ=±1.故本题选B.
因此可得1-λ2=0.解得λ=±1.故本题选B.
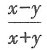
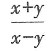
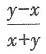
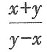
 两边分别对于x求导得
两边分别对于x求导得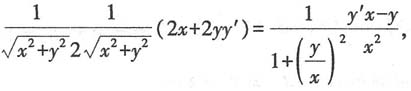 化简可得
化简可得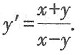 故本题选B.
故本题选B.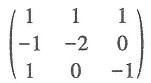

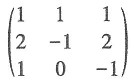

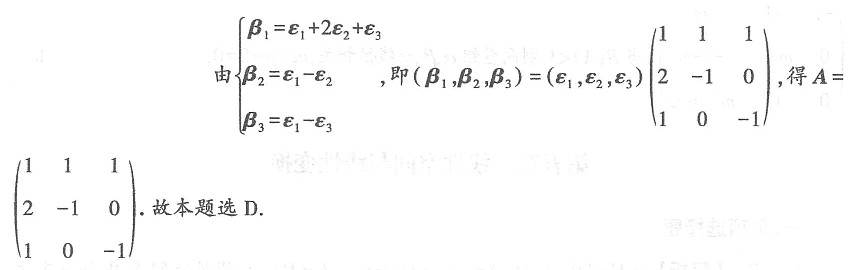
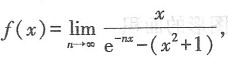 求曲线y=f(x)与直线
求曲线y=f(x)与直线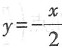 所围成的平面图形绕x轴旋转所围成的旋转体的体积.
所围成的平面图形绕x轴旋转所围成的旋转体的体积.
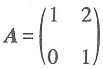 对应的变换作用下变为直线l':x+by=1.
对应的变换作用下变为直线l':x+by=1.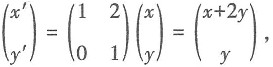 得又点M'(x',y')在l'上,所以x'+by'=1,即x+(b+2)y=1,依题意
得又点M'(x',y')在l'上,所以x'+by'=1,即x+(b+2)y=1,依题意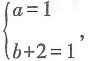 解得
解得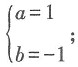
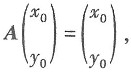 求点P的坐标.
求点P的坐标. 解得y0=0,又点P(x0,y0)在直线l'上,所以x0=1,故点P的坐标为(1,0).
解得y0=0,又点P(x0,y0)在直线l'上,所以x0=1,故点P的坐标为(1,0).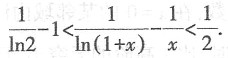
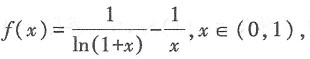 则有
则有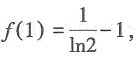
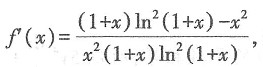 当x∈(0,1)时构造函数φ(x),令φ(x)=(1+x)ln2(1+x)-x2,x∈(0,1),φ'(x)=ln2(1+x)+2ln(1+x)-2x,x∈(0,1),
当x∈(0,1)时构造函数φ(x),令φ(x)=(1+x)ln2(1+x)-x2,x∈(0,1),φ'(x)=ln2(1+x)+2ln(1+x)-2x,x∈(0,1),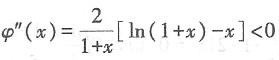 成立,∴
成立,∴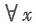 ∈(0,1)时,φ'(x)单调递减,即x∈(0,1)时,φ'(x)<φ'(0)=0,由此可得φ(x)单调递减,即x∈(0,1)时,φ(x)<φ(0)=0,也就是说在(0,1)上,(1+x)ln2(1+x)-x2<0,即f(x)<0,知f(x)单调递减,从而
∈(0,1)时,φ'(x)单调递减,即x∈(0,1)时,φ'(x)<φ'(0)=0,由此可得φ(x)单调递减,即x∈(0,1)时,φ(x)<φ(0)=0,也就是说在(0,1)上,(1+x)ln2(1+x)-x2<0,即f(x)<0,知f(x)单调递减,从而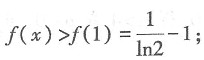 又因为
又因为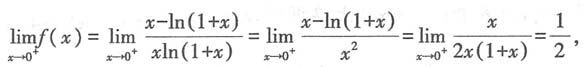 当x∈(0,1)时,f'(x)<0,知f'(x)单调递减,且
当x∈(0,1)时,f'(x)<0,知f'(x)单调递减,且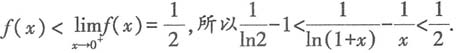
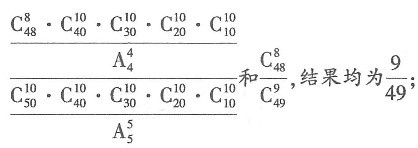 所以k=5,并采取“10合1检测法”,求共检测15次的概率为
所以k=5,并采取“10合1检测法”,求共检测15次的概率为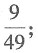

 的值.
的值.
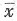 表示一组数据的平均数,每个数据与它们的平均数
表示一组数据的平均数,每个数据与它们的平均数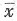 的差的平方分别是
的差的平方分别是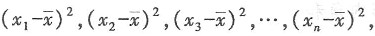 我们用这些数的平均数,即用
我们用这些数的平均数,即用 来衡量这组数据的波动的大小,并把它叫作这组数据的方差,记作s2.
来衡量这组数据的波动的大小,并把它叫作这组数据的方差,记作s2.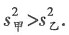 这时在图形语言、符号语言和文字语言的三种表征下,学生能清晰地分辨,甲种玉米方差较大,波动较大,不稳定;乙种玉米方差较小,波动较小,较稳定.
这时在图形语言、符号语言和文字语言的三种表征下,学生能清晰地分辨,甲种玉米方差较大,波动较大,不稳定;乙种玉米方差较小,波动较小,较稳定.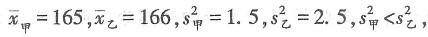 从而得出甲芭蕾舞团女演员的身高更整齐.
从而得出甲芭蕾舞团女演员的身高更整齐.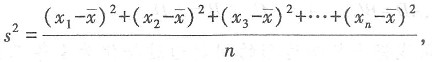 式中的s2表示方左,x1,x2,x3…xn表示样本中的各个数据,
式中的s2表示方左,x1,x2,x3…xn表示样本中的各个数据,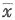 表示样本平均数;
表示样本平均数;